Gli urti
Spesso abbiamo bisogno di conoscere coma una forza dipende dal tempo,
in quanto risolvere il problema utilizzando le reazioni energetiche non è
possibile o sufficiente. Introduciamo allora la seguente quantità vettoriale
chiamata impulso.
r
t1 r
p1
r t1 r
dp
r r r
r
J = ∫ F (t )dt = ∫ dt = ∫ dp = p1 − p0 = ∆p
t0
t0
dt
r
p0
Dimensionalmente I è equivalente a p e quindi si misura in N·s. I misura
la variazione di quantità di moto e quindi, se un sistema è isolato, I è
nullo. La definizione data per l’impulso prende il nome di teorema
dell’impulso.
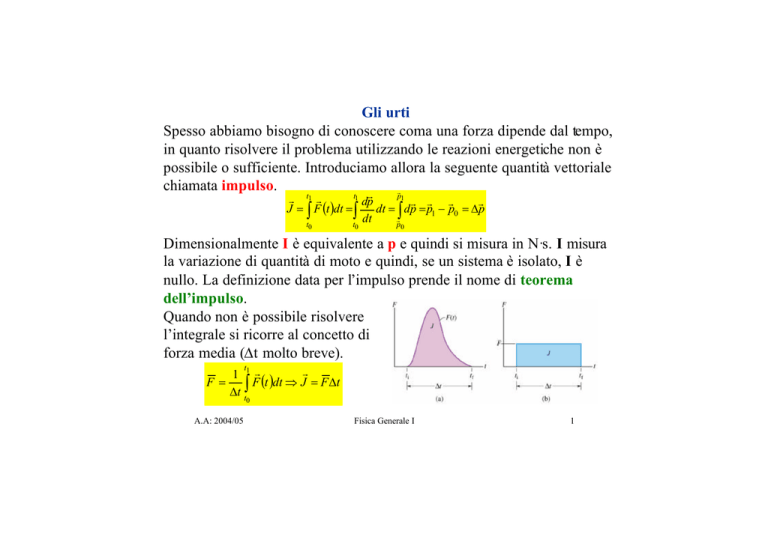
Quando non è possibile risolvere
l’integrale si ricorre al concetto di
forza media (∆t molto breve).
t
r
1 1 r
(
)
F=
F
t
dt
⇒
J
= F ∆t
∆t t∫
0
A.A: 2004/05
Fisica Generale I
1
Urto: evento isolato durante il quale una forza relativamente intensa
agisce, per un tempo relativamente breve, su entrambi i corpi
che entrano in contatto
Nella trattazione degli urti si fanno le seguenti ipotesi:
1. Non possiamo conoscere nel dettaglio
ciò che avviene all’istante dell’urto,
ma possiamo determinare lo stato del
sistema subito prima e subito dopo
l’urto;
2. L’urto avviene in un tempo brevissimo
durante il quale i due corpi non si
muovono l’uno rispetto all’altro e
quindi la loro energia potenziale non
varia.
A.A: 2004/05
Fisica Generale I
2
Consideriamo due corpi che interagiscono solamente tra di loro (sistema
isolato), indichiamo con p1 e p2 le quantità di moto di ciascun corpo
r
r
r
r
dp1
dp2
F12 (t ) =
= − F21(t ) = −
dt
dt
r
r
dp1 dp2
+
= 0 il sistema è isolato
dt
dt
r
r
J12 = − J 21
Possiamo quindi affermare che, quando due corpi formanti un sistema
isolato, interagiscono (urto)
r
r
∆p1 = −∆p2
A.A: 2004/05
I due corpi si scambiano quantità di moto
Fisica Generale I
3
In seguito al processo d’urto, due corpi possono mantenere le masse
possedute originariamente, possono variare la prorpia massa, oppure
possono dar luogo ad un corpo unico di massa pari alle due masse iniziali
Urto elastico
Urto anelastico
EK i = E K f
E K i ≠ EK f
m1i = m1 f
m1i ≠ m1 f
m2i = m2 f
m2i ≠ m2 f
Se m1i + m2i =Mf, allora si parla di urto completamente anelastico.
Se il sistema è isolato, sappiamo che la quantità di moto del sistema si
conserva e questo indipendentemente dal fatto che l’urto sia elastico
o aneleastico.
I due tipi di urto si differenziano per la conservazione dell’energia, che si
riduce alla sola energia cinetica per l’ipotesi fatta che nell’urto non vari
l’energia potenziale.
L’energia cinetica si conserva solo nell’urto elastico
A.A: 2004/05
Fisica Generale I
4
Pertanto, se due corpi costituenti un sistema isolato e chiuso si urtano
elasticamente, possiamo scrivere
r r
Il secondo gruppo di equazioni
Pi = Pf
corrisponde a quattro equazioni
E
=
E
Kf
Ki
scalari e contiene 6 incognite
r
r
r
r
(ammesso che si conoscano le
m1v1i + m2v2i = m1v1 f + m 2v2 f
velocità iniziali come vettori), di
1
1
1
1
2
2
2
2
2 m1v1i + 2 m2v2i = 2 m1v1 f + 2 m2v 2 f conseguenza il sistema risulta
indeterminato.
Per avere una soluzione bisogna imporre degli ulteriori vincoli al sistema,
ad esempio possiamo conoscere le velocità iniziali e limitarci a trattare
urti in una sola dimensione. Otteniamo così
v1 f =
v2 f =
A.A: 2004/05
(m1 − m2 )v1i + 2m2v2i
m1 + m2
2 m1v1i + (m2 − m1 )v2i
m1 + m2
Fisica Generale I
5
Casi particolari
1. m1 = m2 = m
v 1f = v2i e v 2f = v1i scambio di velocità
1
2
prima
v 1i
v 2i
1
2
dopo
v 2i
v 1i
2. m1 >> m2
v 1f ≈ v 1i e v2f = 2v1i –v2i
1
2
v 1i
1
prima
v 2i
2
v 1f
A.A: 2004/05
v1 resta invariata
dopo
v 2f
Fisica Generale I
6
3. m1 << m2 e v2i=0
v 1f = -v 1i e v2f ≈ 0
m1 rimbalza all’indietro,m2 resta fermo
1
prima
v 1i
1
dopo
-v 1i
4. Urto obliquo contro una parete piana immobile e liscia
(si risolve solo nel caso bidimensionale conoscendo v1i)
L’angolo di incidenza è θ⇒v isinθ e
vf
v
sinθ
vicosθ. Parallelamente alla parete non
f
v fcosθ
c’è forza impulsiva ⇒P|| si conserva
θ
(v isinθ), mentre in direzione ⊥ alla
θ vi
parete si cade nel caso 3. v icosθ =
v isinθ
− vicosθ; si può osservare che |v i| = |v f|
v icosθ
e le velocità formano sempre un angolo
θ con la ⊥ alla parete
A.A: 2004/05
Fisica Generale I
7
Consideriamo ora un sistema chiuso e non isolato. Se due corpi si urtano
elasticamente possiamo ancora parlare di conservazione della quantità di
moto?
Dobbiamo innanzitutto distinguere tra le forza impulsive e le forze non
impulsive.
F impulsiva
• F ≠ 0 solo nel tempo ∆t in cui
avviene l’urto
• |F| molto elevato in ∆t
• J molto grande
• ∆p importante
F non impulsiva
• F ≠ 0 sempre
• |F| moderato
• J molto piccolo
• ∆p trascurabile
imp
F(t)
A.A: 2004/05
J non imp
Fisica Generale I
8
Allora se abbiamo forze esterne non impulsive possiamo ancora parlare
di conservazione di P, mentre nel caso di forze esterne impulsive
(come ad esempio le reazioni vincolari sollecitate nell’urto) non si può
parlare di conservazione di P (P si può solo conservare parzialmente).
Sistema isolato
Urto elastico
Si conservano P ed EK
Urto anelastico
Si conserva P, non si conserva EK. Se l’urto è
completamente anelastico, l’energia dissipata
corrisponde all’energia interna del sistema
Sistema non isolato
Forze non impulsive Tutto come nel sistema isolato
Forze impulsive
A.A: 2004/05
P al più si conserva parzialmente
Fisica Generale I
9












