Lezione Termodinamica

Lezione
Termodinamica
1
Sistemi termodinamici
La termodinamica si occupa delle interazioni tra corpi macroscopici che comprendono sia scambi di energia meccanica sia scambi di calore (energia termica),
e storicamente nasce assieme allo sviluppo della macchina a vapore, dunque con
lo scopo di studiare la possibilità di convertire con la massima efficienza il calore
in energia meccanica. È dunque una scienza che nasce come esigenza empirica,
diversa dallo studio delle proprietà fondamentali della materia. In effetti la termodinamica come viene comunemente intesa riguarda la descrizione dal punto
di vista dei comportamenti macroscopici di insiemi di corpi o sostanze costituite
da numeri enormi di costituenti microscopici, dei cui dettagli ci disinteressiamo
– perché per noi non misurabili, o perché ingestibili dato il numero enorme di
costituenti coinvolti (dell’ordine del numero di Avogadro).
Un sistema termodinamico è di solito definito come un insieme di corpi
completamente descritto dal punto di vista macroscopico - da un certo numero
(in genere non molto grande) di variabili, dette variabili di stato.
In realtà da un punto di vista generale possono essere considerati sistemi
termodinamici anche insiemi di corpi molto complessi, per esempio la Terra, o
il sistema solare, o l’intero universo. L’importante, per definire un sistema, è
definirne i confini, cioè stabilire in modo non ambiguo se un dato corpo o una
data porzione di sostanza appartiene al sistema o al resto dell’universo (ambiente
esterno).
Una bottiglia piena d’aria, per esempio, può essere considerata un sistema
termodinamico, anche quando è aperta: l’importante in questo caso è stabilire
un confine (anche solo geometrico e non fisico) per decidere se una porzione di
aria si trovi all’interno o all’esterno del sistema.
I sistemi si possono classificare secondo il tipo di interazioni che possono
avere con l’ambiente esterno:
• un sistema è aperto se può scambiare energia e materia con l’esterno (per
esempio una bottiglia aperta, o un organismo biologico);
• un sistema è chiuso se può scambiare energia ma non materia con l’esterno
(per esempio una bottiglia chiusa, un palloncino pieno di gas o di acqua);
• un sistema è isolato meccanicamente se è chiuso e non può scambiare
energia meccanica con l’esterno (per esempio un fluido contenuto in un
recipiente fermo e dalle pareti rigide);
1
• un sistema è isolato termicamente se è chiuso e non può scambiare
energia termica (calore) con l’esterno (per esempio un fluido contenuto in
un recipiente dalle pareti isolanti);
1.1
Variabili di stato, funzioni di stato
Lo stato di un sistema è definito dai valori delle variabili di stato che permettono di descriverlo completamente dal punto di vista macroscopico. Un fluido
contenuto in un recipiente dato, per esempio, sarà descritto da variabili come
la massa totale, il volume, la temperatura, la densità, la pressione. In altri
termini, due copie dello stesso sistema in cui tutte le variabili di stato hanno
lo stesso valore devono essere indistinguibili dal punto di vista dell’osservazione
macroscopica.
Le variabili termodinamiche si dividono in due categorie a seconda del loro comportamento in funzione delle dimensioni del sistema. Immaginiamo di
prendere un sistema omogeneo (suddivisibile in tante piccole parti tutte identiche) e raddoppiarlo, semplicemente affiancandolo a una copia identica. Se cosı̀
facendo la variabile considerata raddoppia, è una variabile estensiva, cioè proporzionale alle dimensioni del sistema. Se invece la variabile rimane la stessa, si
tratta di una variabile intensiva. Sono variabili estensive il volume, il numero
di moli e l’energia totale di un sistema, mentre sono intensive la pressione e la
temperatura.
Non tutte le variabili di stato sono indipendenti: possono essere legate da
un’equazione di stato come nel caso dei gas perfetti, in cui pV = nRT lega tra
loro la pressione di un gas, il suo volume, la sua temperatura e la sua massa
(espressa in numero di moli).1 Lo stato del sistema costituito da un dato numero
di moli di gas perfetto, dunque, può essere specificato completamente dai valori
di due variabili a scelta tra p, V, T , dato che la terza è legata alle altre due
dall’equazione di stato. In generale lo stato di un sistema può essere quindi
rappresentato da un punto in uno spazio cartesiano che ha sugli assi i valori
delle variabili di stato.
Una grandezza fisica relativa al sistema è funzione di stato quando può essere
espressa come funzione delle variabili di stato: il suo valore dipende quindi solo
dallo stato in cui si trova il sistema, indipendentemente dalla storia del sistema
stesso. Se un sistema si trova nello stato A e poi vi ritorna dopo essersi trovato
in un altro stato B tutte le funzioni di stato riassumono lo stesso valore.
1.2
Sistemi in equilibrio
Noi ci occuperemo quasi esclusivamente di sistemi termodinamici in equilibrio,
sia tra le varie parti del sistema, sia tra il sistema e l’esterno. Un sistema (o una
sua parte, è in equilibrio) se il suo stato è stazionario, ossia non varia nel tempo
(le variabili di stato non dipendono dal tempo) e se non ha scambi macroscopici
netti di energia o materia con le altre parti del sistema o con l’esterno.
L’equilibrio può essere di vari tipi:
1 Una
mole di una sostanza di composizione chimica nota è una quantità pari al peso
molecolare medio espresso in grammi, e corrisponde (entro la precisione sperimentale) a un
numero di Avogadro di molecole NA ≈ 6 × 1023
2
• equilibrio meccanico: la forza totale e il momento delle forze agenti sul
sistema (e su ogni sua porzione) sono nulli. Questo implica per esempio,
come abbiamo visto, che all’interno di un fluido la pressione deve essere
uniforme (trascurando l’effetto della gravità). Inoltre se il sistema non
è meccanicamente isolato, le forze di pressione sulle pareti devono essere
bilanciate: questo implica per esempio che se il sistema è costituito da due
camere separate da una parete mobile, la pressione ai due lati della parete
deve essere la stessa; se il sistema è rappresentato da un gas in un cilindro
chiuso da un pistone, l’equilibrio meccanico richiede che la pressione del
gas sia uguale alla pressione esterna, e cosı̀ via.
• equilibrio termico: non ci sono più scambi di calore netti tra le varie parti
del sistema, o tra il sistema e l’esterno. Questo implica che la temperatura
deve essere uniforme all’interno del sistema e, se questo non è isolato
termicamente, deve essere uguale a quella dell’ambiente esterno.
• equilibrio diffusivo e equilibrio chimico nel caso in cui siano possibili
scambi di materia o reazioni chimiche tra il sistema e l’esterno, o tra le
varie parti del sistema. Si raggiunge quando la quantità netta di materia
di ogni componente del sistema non varia più nel tempo. Noi non ci
occuperemo di sistemi in cui questi scambi sono possibili.
1.3
Trasformazioni termodinamiche
Si chiamano trasformazioni termodinamiche le variazioni dello stato del sistema
(e quindi delle variabili e delle funzioni di stato). Per esempio, data una certa quantità di gas contenuta in un recipiente ermeticamente chiuso, ne si può
variare lo stato scaldandolo, o comprimendolo, o entrambe le cose.
Una particolare categoria di trasformazioni, impossibili da realizzare in pratica ma utili come casi limite, è rappresentata dalle trasformazioni reversibili.
Una trasformazione è reversibile se
• è quasistatica, ossia estremamente (infinitamente) lenta, in modo tale che
in ogni istante il sistema si possa considerare all’equilibrio tra le sue parti
e con l’ambiente esterno;
• le cause che la provocano sono infinitamente deboli
• in ogni momento della trasformazione il verso di quest’ultima si può invertire con un cambiamento infinitamente piccolo delle cause esterne
Se una trasformazione non soddisfa questi criteri (idealizzati) è detta irreversibile (tutte le trasformazioni reali, in particolare quelle spontanee, lo sono: più sono lente, tuttavia, più si avvicineranno alla situazione limite della
trasformazione reversibile).
La compressione di un gas in un cilindro chiuso da un pistone sarà reversibile
se avviene in modo molto lento, tale che in ogni istante la pressione esterna
applicata al pistone sia uguale a quella interna del gas. Allo stesso modo un
riscaldamento attraverso lo scambio di energia termica sarà reversibile se in ogni
istante la temperatura del sistema sarà uguale a quella del corpo esterno con
cui scambia calore.
3
Naturalmente, affinché la trasformazione proceda in un verso anziché nel
verso opposto (e quindi per esempio il gas venga compresso e non espanso) sarà
necessario che la pressione esterna superi anche se di poco quella interna, ma il
limite di trasformazione reversibile è per l’appunto quello in cui questa differenza
di pressione (la “causa” che provoca la trasformazione) è infinitamente piccola e
tende a zero; per invertire il verso della trasformazione la differenza di pressione
dp deve passare da positiva e molto piccola a negativa e molto piccola: è questo
che si intende con “cambiamento infinitamente piccolo” delle cause.
La compressione di un gas ottenuta appoggiando un peso sul pistone, o il
suo riscaldamento ottenuto immergendo il recipiente nell’acqua bollente, sono
esempi di trasformazioni decisamente irreversibili.
Le trasformazioni reversibili di un sistema (e solo quelle!) si possono rappresentare come curve continue nello spazio delle variabili di stato. Una trasformazione è ciclica se lo stato finale coincide con quello iniziale: se la trasformazione
è reversibile è rappresentata nello spazio delle variabili di stato da una curva
chiusa.
2
Primo principio della termodinamica
Il primo principio della termodinamica afferma che l’energia si conserva, a patto
di includere negli scambi energetici anche gli scambi di calore, identificato come
una delle forme che può assumere l’energia (grazie agli esperimenti di Joule).
Per un dato sistema, il primo principio si esprime convenzionalmente cosı̀:
∆U = ∆Q − ∆L
(1)
La variazione di energia totale (o energia interna) di un sistema in una
trasformazione (finita o infinitesima) è uguale alla differenza tra la quantità di
calore (energia termica) assorbito ∆Q e il lavoro ∆L compiuto dal sistema verso
l’esterno (energia meccanica).
È fondamentale osservare che l’energia totale di un sistema (che in ultima
analisi, dal punto di vista microscopico, è la somma delle energie meccaniche dei
suoi costituenti) è, come in meccanica, una funzione di stato.2 La variazione
di energia interna dipende solo dallo stato finale e da quello iniziale, mentre il
lavoro compiuto e il calore assorbito dalla trasformazione, dunque dal cammino
seguito per andare dallo stato iniziale a quello finale.
3
Gas perfetti
Il gas perfetto, o ideale, è per definizione un gas che obbedisce alla legge dei gas
perfetti, verificata sperimentalmente per tutti i gas sufficientemente rarefatti.
Per una data quantità di gas individuata dal numero n di moli, l’equazione è,
come sappiamo
pV = nRT
2 Lo stato di un sistema in meccanica è specificato conoscendo a un dato istante la posizione
e la quantità di moto di tutte le particelle che lo costituiscono.
4
dove p è la pressione del gas, V il volume, T la temperatura assoluta e R
una costante universale, che vale circa 8.31 J K−1 mol−1 . Dato il sistema chiuso
costituito da un certo numero n di moli di un dato gas, lo stato del sistema è
fissato dai valori di due a scelta delle variabili di stati p, V, T . Tradizionalmente
si scelgono le prime due, e lo stato del sistema è rappresentato da un punto nel
piano cartesiano p, V .
3.1
Diagramma p, V e trasformazioni reversibili notevoli
Una trasformazione reversibile del sistema suddetto è dunque rappresentata
da una curva continua nel piano p, V .
In particolare
• una trasformazione a volume costante o isocora è rappresentata da un
segmento verticale;
• una trasformazione a pressione costante, o isobara, è rappresentata da
un segmento orizzontale;
• una trasformazione isoterma è rappresentata da un segmento di iperbole,
di equazione pV = costante.
Nel corso di una trasformazione, anche se reversibile, il gas scambia in generale energia (meccanica o termica) con l’esterno. In particolare, alle variazioni
di volume è associato uno scambio di energia meccanica (lavoro). Supponiamo per semplicità che il recipiente che contiene il gas abbia una sola parete
mobile (pistone): se perpendicolarmente al pistone agisce una forza esterna F ,
e il pistone si muove di un tratto dx comprimendo il gas, il lavoro compiuto
dalla forza esterna sul sistema sarà dWext = F dx. Se la forza esterna è una
forza di pressione, si ha F = pext S dove S è la superficie del pistone. Dunque
il lavoro compiuto sul sistema vale dWext = F dx = pext Sdx = −pext dV , dove
dV = −dxS rappresenta la variazione (infinitesima) di volume del gas (negativa
se il gas si è compresso, e la forza esterna ha compiuto un lavoro positivo).
Se la trasformazione è reversibile, in ogni istante la forza esterna sul pistone
deve essere controbilanciata dalla forza interna dovuta alla pressione del gas:
in modulo, deve essere pS = |F |. Il lavoro fatto dall’esterno sul sistema vale
dunque in questo caso dWext = −pdV , dove a pe xt abbiamo sostituito il valore
della pressione del gas p. In genere si considera convenzionalmente il lavoro dL
fatto dal gas verso l’esterno (è quello che si vuole ottenere da una macchina
termica), che è l’opposto di quello fatto dall’esterno sul sistema.
In conclusione il lavoro fatto verso l’esterno da un gas il cui volume varia di
dV in una trasformazione reversibile è dato da
dL ≡ −dWext = pdV
Si noti che la formula vale anche se l’espansione non è descritta dal movimento di un pistone (per esempio nel caso di un palloncino che si gonfia), perché
il calcolo si può applicare a ogni piccola porzione di superficie: sommando (integrando) su tutti gli elementini di superficie si ottiene per il lavoro complessivo
lo stesso risultato.
Nel piano p, V il lavoro dL = pdV corrisponde all’elementino di area sottesa
dalla curva della trasformazione. Il lavoro totale compiuto dal gas nel corso di
una trasformazione reversibile uno stato A uno stato B sarà dunque
5
F dx Figura 1: Lavoro fatto dall’esterno su un gas
Z
B
L=
p dV
A
che corrisponde all’area compresa tra la curva e l’asse orizzontale. Nel caso
in cui la curva non sia una funzione che a un valore di V associa un unico
valore di p, si può in genere spezzare il cammino in più tratti per ciascuno dei
quali si calcola l’integrale definito. Se la curva è chiusa (trasformazione ciclica)
l’integrale su tutto il cammino è pari all’area racchiusa dalla linea, presa con il
segno positivo se la linea è percorsa in senso orario, negativo altrimenti.
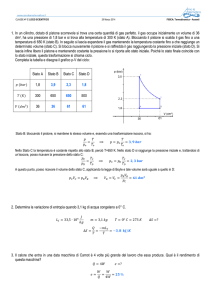
• Esempio: Lavoro compiuto dal gas in un’espansione reversibile isoterma.
Supponiamo che n moli di gas perfetto siano soggette a un’espansione
isoterma reversibile a temperatura T , passando dal volume VA al volume
VB > VA . Il lavoro compiuto dal gas verso l’esterno varrà
Z
B
L=
Z
VB
p dV = nRT
A
Va
VB
1
dV = nRT ln
V
VA
Il lavoro compiuto dal gas per andare da uno stato A a uno stato B dipende
quindi dal cammino percorso: il lavoro non è una funzione di stato.
3.2
Calori specifici
Se un gas perfetto subisce una trasformazione isocora (a volume costante) non
scambia energia meccanica con l’esterno. La sua temperatura però cambia
(proporzionalmente alla pressione, secondo la legge dei gas perfetti), e questo
significa che il gas ha scambiato calore, secondo la formula nota
∆Q = CV ∆T
6
dove la capacità termica è chiamata CV per significare che la trasformazione è
a volume costante. Anche per i gas vale che la capacità termica è proporzionale
alla massa di sostanza, e quindi al numero di moli. Si introduce quindi il calore
specifico molare a volume costante cv , definito come la capacità termica a
volume costante di una mole di gas:
CV = ncV
Notiamo che per una trasformazione a volume costante, poiché ∆L = 0, dal
primo principio della termodinamica si ha ∆U = ∆Q. Dunque
∆U = ncV ∆T
per una trasformazione isocora.
In maniera del tutto analoga si definisce il calore specifico a pressione
costante cp , cosicché per una trasformazione isobara
∆Q = Cp ∆T = ncp ∆T
3.3
Espansione libera nel vuoto
L’energia interna di un gas perfetto è una funzione di stato che dipende solo
dalla temperatura. Questo risultato, a cui si può arrivare per via teorica grazie
a modelli meccanici e statistici, è stato dimostrato sperimentalmente da Joule
prima che tali modelli venissero elaborati, grazie all’esperimento dell’espansione
libera nel vuoto.
L’esperienza consiste nel chiudere una certa quantità di gas in una ampolla
(A) collegata tramite un rubinetto a un’altra (B) in cui è stato fatto il vuoto
(naturalmente non il vuoto assoluto, irrealizzabile nella pratica, ma diciamo una
sua buona approssimazione ai fini dell’esperimento).
A B A B Il gas chiuso nella prima ampolla ha un certo volume V0 = VA e una certa
temperatura T0 , misurabile. Le due ampolle, in ciascuna delle quali è presente
un termometro vengono isolate termicamente dall’esterno, e il rubinetto tra le
due viene aperto, lasciando espandere il gas. Si tratta di un’espansione libera,
un processo veloce e altamente irreversibile.
7
Dopo un certo tempo, quando il gas si è stabilizzato e ha raggiunto un nuovo
equilibrio, esso occupa il volume V1 = VA + VB . La temperatura misurata nelle
ampolle è naturalmente uguale per i due termometri (cosa che non era vera
immediatamente dopo l’apertura, ma che invece sarà vera per definizione al
raggiungimento del nuovo equilibrio). Il risultato non banale è che questa nuova
temperatura T1 è la stessa che il gas aveva prima dell’espansione. Si noti bene
che questo non significa che si è trattato di un’espansione isoterma (men che
meno reversibile): è una trasformazione irreversibile complicata in cui però lo
stato iniziale e quello finale sono caratterizzati da avere volume diverso, ma la
stessa temperatura.
Dal punto di vista energetico, sappiamo che il sistema non ha scambiato
calore con l’esterno, perché è stato isolato termicamente. Dunque ∆Q = 0. Ma
sappiamo anche che ∆L = 0, perchè il gas, pur espandendosi, non ha applicato
alcuna forza su alcuna parete esterna: si è espanso nel vuoto, dunque non ha
compiuto alcun lavoro. Possiamo quindi concludere che ∆U = 0, ossia che
l’energia interna di un numero dato di moli di gas perfetto, che è una funzione
di stato e quindi in generale può essere espressa come U (V, T ), funzione delle
due variabili indipendenti V e T , in realtà non dipende dal volume ed è quindi
U (T ).
Una conseguenza immediata è che dati due stati A e B della stessa quantità di gas perfetto a temperature diverse TA , TB e in generale a volumi diversi VA , VB , la differenza di energia interna tra i due stati dipenderà solo dalla
temperatura e sarà data da
∆U = U (B) − U (A) = ncV (TB − TA )
anche se la trasformazione non è isocora.
Infatti la differenza di energia dipende solo dallo stato finale e dallo stato
iniziale, non dal percorso che li congiunge. Possiamo quindi pensare di portare
prima il gas dallo stato (VA , TA ) allo stato (VB , TA ), che ora sappiamo avere
la stessa energia, e quindi allo stato (VB , TB ) con una trasformazione a volume
costante, in cui ∆U = CV ∆T .
Un’altra conseguenza è che lungo una trasformazione isoterma reversibile si
ha ∆U = 0 e quindi, chiamando sempre A e B lo stato iniziale e quello finale
∆Q = ∆L = nRT ln
VB
VA
dove abbiamo usato il lavoro compiuto lungo un’isoterma, calcolato poco
sopra.
3.4
Relazione tra cp e cV
Il primo principio della termodinamica permette di trovare una semplice relazione che lega il calore specifico (molare) a pressione costante e quello a volume
costante per un gas perfetto.
Consideriamo infatti una mole di gas perfetto (n = 1) che si trova inizialmente nello stato rappresentato dal punto A con coordinate p0 , V0 nel piano
p, V . Se con una trasformazione isobara infinitesima lo portiamo allo stato
C = (p0 , V0 + dV ), avremo per il calore assorbito
dQAC = cp dT = cp [TC − TA ]
8
e per il lavoro compiuto dal gas
dLAC = p0 dV = p0 (VC − VA ) = p0
RTC
RTA
−
p0
p0
= R(TC − TA ) = RdT
Se invece lo portiamo con una trasformazione infinitesima isocora allo stato
B = (p0 , V0 + dV ), abbiamo
dQAB = cV dT = cV [TB − TA ]
e
dLAB = 0
p B dP A C dV V Figura 2: Relazione tra cp e cV
Se scegliamo i punti B e C in modo che abbiano la stessa temperatura
(TB = TC ) (figura 2), l’energia dei due stati finali sarà la stessa, e dunque
dUAB = dUAC . Per il primo principio della termodinamica avremo quindi
dQAC − dLAC = cp dT − RdT = cV dT
da cui otteniamo la relazione cercata fra i calori specifici molari
cp − cV = R
3.5
Equazione dell’adiabatica
Abbiamo visto casi notevoli di trasformazioni termodinamiche reversibili per un
gas perfetto: l’isobara, l’isocora caratterizzata da ∆L = 0, l’isoterma caratterizzata da ∆U = 0. In quale caso ∆Q = 0?
Una trasformazione termodinamica in cui il sistema non scambia calore con
l’esterno è detta adiabatica. Ci chiediamo quale curva nel piano p, V rappresenti una trasformazione adiabatica reversibile per una mole (n = 1) di gas
perfetto.
Per determinarlo usiamo uno stato iniziale A = (p0 , V0 ) e, analogamente
al caso precedente, altri due stati ai vertici di un triangolo rettangolo di area
9
p A dP C B dV V Figura 3: Trasformazione ciclica infinitesima con i punti A e B collegati da una
adiabatica
infinitesima, B = (p0 + dp, V0 + dV ) e C = (p0 + dp, V0 ) (figura 3), in modo tale
che A e B si trovino collegati da un tratto di trasformazione adiabatica.
Consideriamo poi la trasformazione ciclica A → B → C → A. Sappiamo
che in una trasformazione ciclica la variazione netta di energia interna è nulla,
perché l’energia interna è una funzione di stato:
dUAB + dUBC + dUCA = 0
(2)
Consideriamo i singoli tratti:
• A → B è una trasformazione adiabatica (dQBC = 0), dunque
dUAB = −dLAB = −p0 dV
dove abbiamo trascurato l’area del rettangolo ABC che, essendo uguale
in valore assoluto a 12 dp dV , è un infinitesimo di ordine superiore.
• B → C è una trasformazione isobara, dunque
dUBC
= dQBC − dLBC = cp (TC − TB ) − p0 (VC − VB )
cp
=
(pC VC − pB VB ) + p0 dV =
R
cp
= − p0 dV + p0 dV
R
• C → A è una trasformazione isocora (dLCA = 0), dunque
dUCA = dQCA = cV (TA − TC ) =
cV
cV
(pA VA − pC VC ) = − V0 dp
R
R
Imponendo la 2 otteniamo
−p0 dV −
cp
cV
p0 dV + p0 dV −
V0 dp = 0
R
R
cioè
cV V0 dp = −cp p0 dV
10
che si può riscrivere, per un punto qualunque p, V
dp
cp p
=−
dV
cV V
(la curva ha sempre coefficiente angolare negativo), o
cp dV
dp
+
=0
p
cV V
che integrata da uno stato 1 a uno stato 2 dà
ln
p1
cp
V1
+
ln
=0
p2
cV
V2
ossia
p1
p2
V1
V2
γ
=1
da cui
p1 V1γ = p2 V2γ
con
γ≡
cp
R
=1+
>1
cV
cV
per qualunque coppia di stati collegati da una trasformazione adiabatica
reversibile.
In altri termini l’equazione di un’adiabatica nel piano p, V è
pV γ = costante
Sostituendo p = RT /V l’equazione può essere espressa anche come
T V γ−1 = costante
11