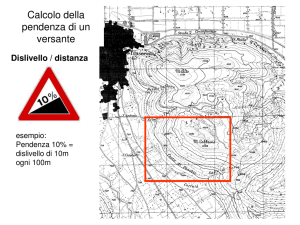
E
Esercitazioni
it i i di Istituzioni
I tit i i di economia
i
Informazioni Generali
Dott. Francesco Caracciolo
Dipartimento di Agraria - Sezione Economia
[email protected]
Tel. ufficio: 081 2539116
Esercitazione del giorno - La domanda
•Curva
Curva di Domanda,
Domanda rappresentazione grafica
ed algebrica.
•Elasticita della domanda al prezzo
Per il conseguimento
g
dell’esame lo studente dovrà
essere in grado di svolgere esercizi della stessa
tipologia di quelli svolti durante le esercitazioni o
assegnatii per casa.
Mi
Micro
Vs
V Macro
M
La Macro-Economia si occupa di grandezze
economiche aggregate; crescita e sviluppo
(recessione, crisi) di un paese, occupazione, liquidità
(debito pubblico).
pubblico)
Indagine della Micro-Economia sono il
comportamento dei singoli operatori economici:
Individui o famiglie se osserviamo il consumo,
imprenditore o imprese se consideriamo la
produzione.
Nell analisi dei Mercati osserverete come i singoli
Nell’analisi
operatori interagiscono fra di loro.
Al b ed
Algebra
d analisi
li i grafica
fi in
i economia
i
Molti dei concetti studiati in economia possono
p
essere espressi attraverso numeri associati a delle
variabili (grandezze che possono assumere diversi
valori). P, Q, C.
Una variabile può assumere valori in risposta a
cambiamenti di altre variabili. Es: relazione fra il costo
di produzione delle mele C, con la quantità prodotta
Q C = 75 + 10Q
delle mele Q,
Le relazioni fra le diverse variabili economiche si
possono rappresentare
t
attraverso
tt
i grafici.
fi i
P d
Pendenza
e derivata
d i t di funzione
f
i
Una p
pendenza stradale del 10%,, significa
g
che una
strada impiega 100 metri per salire in 10 metri in
altitudine. 10/100 = 0.1
ΔY = 10 metri
ΔX = 100 metri
ti
C
C = 75 + 10Q
Q
115€
95€
85€
75€
50€
1
2
4
Q
C l l della
Calcolo
d ll pendenza
d
di una funzione
f
i
Le relazioni lineari hanno una pendenza costante
definita come: ΔY/ΔX
La pendenza è il rapporto fra il cateto verticale
con q
quello orizzontale.
Es: da Q1=2 a Q2=4;
ΔX = Q2 - Q1= 4-2 = 2
ΔY= C2-C1 =115 – 95 = 20
ΔY/ΔX = 20/2 = 10
P d
Pendenza
e derivata
d i t di funzione
f
i
La pendenza di una curva in un punto si chiama derivata della
funzione in quel punto. La derivata è anch’essa funzione di x, in
quanto punto per ogni x, assume un valore. Quindi la derivata
della funzione y = f(x)
( ) è una funzione di x e si indica con la
scrittura y = f΄ (x).
La derivata della funzione si può anche esprimere con la
notazione,
t i
dy
d
dx
≡ f΄ (x) ≡
Δy
lim
Δx → 0 Δx
ovvero rapporto di ΔY/ΔX con ΔX infinitesimale.
D i t di funzione
Derivata
f
i
– esempii
dp
es : p = a - bq ;
= −b
dqq
dc
c = 75 + 10q ;
= 10
dq
La funzione di Domanda
qx = ƒ(px,R,)
• Ri
Risultato
lt t di un processo decisionale
d i i
l
del consumatore (massima utilità
complessiva
l
i entro
t il limite
li it del
d l bilancio)
bil
i )
• Ci indica come il consumatore sceglie
ll’ammontare
ammontare ottimo del bene x da
consumare, al variare del prezzo del
bene (px),
) del suo reddito (R).
(R)
La funzione di Domanda
qx = ƒ(px,R)
C
Complicazioni
li i i
qx = ƒ(px,R,py, pz, K)
py, pz: prezzi altri beni
K: caratteristiche socio-demografiche-psicografiche
gg
individuo ((riferimenti valoriali, atteggiamenti,
opinioni, stili di vita)
Capacità di
spesa
10€
P= 2.5€
P
P= 10€
1
P= 2€
2
4
Quantità di
gelati
Se la funzione di domanda è
p
q= f(p)
Noi rappresentiamo graficamente la
funzione di domanda INVERSA
10€
p= f(q)
5€
2.5€
1
2
4
Quantità di
gelati
La funzione di domanda
Prezzo
Sulla funzione di domanda tra prezzo e
quantità c’è
c è una relazione negativa
p1= 10 €
q = a-bp
a bp (diretta)
Formulazioni
p = a-bq
q
(inversa)
p2= 5 €
Pendenza
p3= 3 €
0
10
14
Quantità
-b =
Δq
Δp
Parliamo di relazione di dipendenza diretta fra due variabili X
ed Y quando ad un incremento di X è sempre associato un
incremento di Y e viceversa. Il grafico di questa relazione avrà
una pendenza positiva.
Si parla di relazione di dipendenza negativa
fra la variabile X and Y,
Y quando un incremento di
X è sempre associato ad un decremento di Y ed
un decremento di X è associato ad un
incremento di Y. Il grafico avrà una pendenza
negativa.
La Domanda è puna funzione inversa del prezzo
10€
p = a-bq
5€
2.5€
1
2
4
Quantità di
gelati
La Domanda è una funzione inversa del prezzo
Curva di domanda inversa, che identifica il prezzo
corrispondente ad ogni quantità domandata dai
consumatori.
p = a-bq
Curva di domanda diretta, che identifica, per ogni
livello del prezzo, qual è la quantità che i consumatori
sono disposti ad acquistare.
q = (a/b) – (p/b)
La Domanda è una funzione inversa del prezzo
Un esempio
p = a-bq
p = 10-1/2q
p
q = 20-2p
p= 10
p
p= 5
0
10
20
q
p
q
10
0
5
10
0
20
La Domanda è una funzione inversa del prezzo
Un esempio
p = a-bq
p = 10-0.5q
p
q = 20-2p
p= 10
p
p= 5
0
10
20
q
p
q
10
0
5
10
0
20
Esercizio
Si considerino i seguenti dati:
P (prezzo del bene) = 3
Data la funzione di domanda: q ≡ 20 – 2p
a )Determinare le quantità consumate del
bene q
b) Determinare le quantità consumate del
bene q con p = 5, p = 6.
Esercizio
Determinare le quantità consumate del bene con p = 3, p =
5, p =6.
6.
q ≡ 20 – 2 p
p
q*
3
14
5
10
8
4
10
0
p
8€
Esercizio (1c)
Rappresentate
graficamente i punti
trovati.
5€
3€
4
10
14
Q
Esercizio
• U
Un iindividuo
di id h
ha lla ffunzione
i
di d
domanda
d relativa
l i alla
ll bi
birra
uguale a
q x = 25 − 20 Px
dove Px il prezzo della birra e qx la quantità di birra
consumata.
a) Calcolate la quantità consumata di birra.
b.) Calcolate la funzione di domanda inversa.
c.) Disegnare la curva di domanda.
q x = 25 − 20 Px
q x = 25 − 20
qx = 25 -20 = 5
Calcolate la funzione di domanda inversa
qb = 25 − 20 Pb
qb + 20 Pb = 25
20 Pb = 25 − qb
25 − qb
Pb =
20
Disegnare la curva di domanda…
qb = 25 − 20 Pb
25 − qb
Pb =
20
pb
qb *
0.8
9
1
5
12
1.2
1
Possiamo vedere come cambia la quantità consumata dal consumatore del
bene q al variare del suo p
prezzo
Disegnare la curva di domanda…(inversa)
Esercizio (2)
•
Due C
D
Consumatorii (A) e (B) con ffunzioni
i i di d
domanda
d
inversa rispettivamente pari a:
P = 15 − q A
P = 24 − 4 q B
Si calcolino analiticamente le funzioni di domanda dei
due consumatori e la funzione di domanda
aggregata.
aggregata
P = 15 − q A
qA
qB
qtot
1
14
5 75
5,75
19,75
P = 24 − 4 q B
2
13
5,5
18,5
4 q B = 24 − P
3
12
5,25
17,25
qB = 6 − 1/ 4P
4
11
5
16
5
10
4,75
14,75
q A = 15 − P
qA + qB = 15 − P + 6 − 1 / 4P
qA + qB = 21− 5 / 4P
p
La Domanda di mercato è la somma orizzontale delle domande
individuali
P
24
p = 24 – 4qB
p = 15 - qA
qA = 15 - p
p = 24 - 4qB
qB = 6 - 0,25p
qA+B = 21 - 1,25p
che vale per
q >2,5 e p <10
15
0
2,25
6
15
21
Q
Esercizio (2)
•
Un iindividuo
U
di id h
ha lla ffunzione
i
di d
domanda
d relativa
l i alla
ll bi
birra
uguale a
q b = 25 − 20 Pb
dove Pb il prezzo della birra e qb la quantità di birra
consumata.
- Calcolate l’elasticità della domanda rispetto al prezzo
per P= 1€ e ∆P = 0.1
Calcolo dell’elasticità
dell elasticità della domanda
Δq p
ηp =
⋅
Δp q
/
η p = (pendenza funzione di domanda) · (p/q)
E’ la Reattività del consumo rispetto al prezzo.
E
prezzo
L’attesa variazione percentuale delle quantità consumate di
q, rispetto ad una variazione percentuale del prezzo dello
stesso prodotto.
pb
qb *
08
0.8
9
1
5
1.1
3
Δq p
ηp =
⋅
Δp q
Δq
q 3−5
=
= −2 / 0.1 = −20
Δp
p 1.1 − 1
pb
qb *
ηp
0 625
0.625
12 5
12.5
-11
0.8
9
-1.78
1.78
1
5
-4
1.1
3
-7.3
p
η p = −20 ⋅
q
Calcolo dell’elasticità
dell elasticità della domanda
qb = 25 − 20 Pb
Δq p
ηp =
⋅
Δp q
1
= - 20 · = - 4
5
Es: Se il prezzo aumenta del 10%, la
quantità consumata diminuisce del 40%
Verifichiamo
Pb = 1€, 1.1€
Q=5,
3
qb = 25 − 20 Pb
qb= 25
25– 20
20·(1.1)
(1.1) = 25 – 22 = 3
Es: Se il prezzo aumenta del 10%, la
quantità consumata diminuisce del 40%
(5-3)/5
/ = 0.4
Aumentando
A
d il prezzo d
dell 10% (d
(da 1€ a 1.1€)
1 1€) lla
quantità domandata qb passa da 5 a 3 (- 40%).
L’elasticità della domanda rispetto al
prezzo(ηp) è pari a -4
Domanda elastica ed inelastica
Domanda elastica
la domanda
d
d reagisce sensibilmente al prezzo.
Domanda perfettamente elastica
la variazione della domanda ad una variazione del
prezzo e’ infinita (η → ∞)
Domanda con elasticità unitaria
la domanda varia nella stessa percentuale del prezzo (η
= 1)
Domanda inelastica
la domanda non reagisce sensibilmente al prezzo.
D
Domanda
d perfettamente
f tt
t inelastica
i l ti (rigida)
( i id )
La domanda è indipendente dalla variazione del prezzo
(η = 0)
Esercizio (3)
Sia data la seguente funzione di domanda:
P= 1/8 Q2 – 3Q
Q + 10 ((0≤Q≤4))
a)Si calcoli l’elasticità puntuale per Q= 2 e ∆ Q = 2
b) Si calcoli ll’elasticità
elasticità puntuale per Q = 2 e ∆ Q = 1
SVOLGIMENTO
P= 1/8 Q2 – 3Q + 10
Si calcola P con Q = 2
P = 1/8 × 22 − 3×2 + 10 = 4,5
Si calcola P con Q = 2 + ∆ Q =4
P = 1/8 × 42 − 3×4 + 10 = 0
Si calcola ∆P = p2-p1
0-4 5 = -4,5
0-4,5
-4 5
Si risolve la formula dell’elasticità
Δq p
ηp = ⋅
Δp q
Δq p
ηp = ⋅
Δp q
η p = (2 /− 4,5) ⋅ (4,5 / 2) = −1