Confronto tra gli elementi di un triangolo

Geometria piana per la Prima Classe del Liceo
Confronto tra gli elementi di un triangolo
Problema
Sai ABC un triangolo qualsiasi con AB < AC e AM la mediana relativa al lato BC. Prolungare AM dalla parte di
M del segmento MD congruente ad AM.
Dimostrare che DCAB e che l’angolo BAM è maggiore dell’angolo CAM.
Dimostrazione
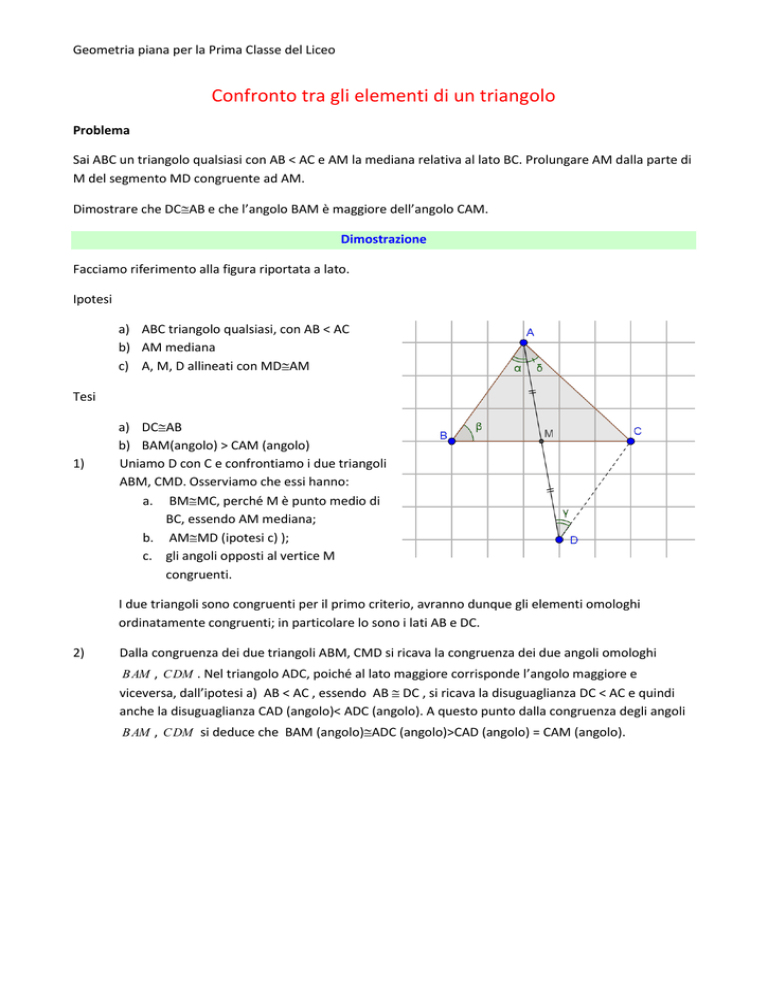
Facciamo riferimento alla figura riportata a lato.
Ipotesi
a) ABC triangolo qualsiasi, con AB < AC
b) AM mediana
c) A, M, D allineati con MDAM
Tesi
1)
a) DCAB
b) BAM(angolo) > CAM (angolo)
Uniamo D con C e confrontiamo i due triangoli
ABM, CMD. Osserviamo che essi hanno:
a. BMMC, perché M è punto medio di
BC, essendo AM mediana;
b. AMMD (ipotesi c) );
c. gli angoli opposti al vertice M
congruenti.
I due triangoli sono congruenti per il primo criterio, avranno dunque gli elementi omologhi
ordinatamente congruenti; in particolare lo sono i lati AB e DC.
2)
Dalla congruenza dei due triangoli ABM, CMD si ricava la congruenza dei due angoli omologhi
B AM , C DM . Nel triangolo ADC, poiché al lato maggiore corrisponde l’angolo maggiore e
viceversa, dall’ipotesi a) AB < AC , essendo AB  DC , si ricava la disuguaglianza DC < AC e quindi
anche la disuguaglianza CAD (angolo)< ADC (angolo). A questo punto dalla congruenza degli angoli
B AM , C DM si deduce che BAM (angolo)ADC (angolo)>CAD (angolo) = CAM (angolo).