LABORATORIO 2 (meccanica e Termodinamica) a.a. 2007/2008 F.Balestra.
( Per cortesia segnalatemi punti non chiari o refusi. Grazie e buon studio)
Metodo dei Minimi Quadrati .
Principio di Massima Verosimiglianza .
Test del χ2.
c 2 0.95H4L = 0.711 and c 2 0.05H4L = 9.488
density function and distribution function
1.0
0.3
0.8
0.2
0.6
0.1
0.4
0.2
2
10
20
30
40
50
4
6
8
10
12
- 0.1
9
8
7
6
5
4
3
4
5
6
7
8
Metodo dei Minimi Quadrati e Principio di Massima Verosimiglianza.
Proprieta’ degli stimatori.
Dipendenza della matrice di covarianza e del χ2 dall’errore sulle y.
Test del χ2.
Ricerca della migliore forma funzionale.
Correlazioni tra i coefficienti stimati.
Principio di Massima Verosimiglianza.
Media pesata. Stima di parametri per la distribuzione di Bernoulli e di Poisson.
Stima e proprieta’ degli stimatori.
1
Principio di massima verosimiglianza e metodo dei minimi quadrati.
Supponiamo di avere n coppie di dati {xi; yi ± σi}
Sia y = f( x; a ) una funzione che fornisce un valore y per ogni x. La forma e’ nota, ma contiene un
parametro a ( o piu’ parametri) che vogliamo stimare.
Le misure yi hanno come valore vero y = f( xi;a) e sono disperse rispetto ad y a causa dell’errore σi,
con distribuzione gaussiana.
La probabilita’ di ottenere un particolare valore di yi per un dato valore di xi e’
−
[ yi − f ( xi ; a )]2
1
2σ i2
e
dyi .
σ i 2π
La probabilita’ congiunta di ottenere la serie delle n misure indipendenti {yi} realmente ottenute
vale
P ( yi ; a ) =
P = ∏1 P( yi ; a ) = (∏1
n
n
dyi
)•e
σ i 2π
−
n
∑
1
[ yi − f ( xi ; a )]2
2σ i2
La funzione densita’ di probabilita’ corrispondente,detta a posteriori perche’ costruita con il
campione di dati, e’ la funzione di verosimiglianza L per il campione di dati. Essa vale
−
n
∑
[ yi − f ( xi ; a )]2
1
2σ i2
.
L = ∏1 P( yi ; a ) = (∏1
)•e 1
σ i 2π
Il Principio di Massima Verosimiglianza assume che il valore piu’ verosimile come stima del
parametro a e’ quello che rende massima la funzione L, ossia rende massima la probabilita’ di
ottenere la serie di dati del campione .
Massimizzare L e’equivalente a rendere massima la funzione logaritmo l = ln L:
n
n
n
[ yi − f ( xi ; a )]2
n
1
1 n [ yi − f ( xi ; a )]2
l = ln L = ln ∏1 P ( yi ; a ) = ∑ ln[(
)−∑
]
ln[
(
2
)
σ
π
=
−
−
∑
∑
i
1
21
2σ i2
σ i2
σ i 2π
1
1
n
n
.
Per rendere massima l e’ sufficiente minimizzare la sommatoria:
n
2
[ yi − f ( xi ; a )]2
,
χ =∑
2
1
σ
i
cioe’ minimizzare la somma del quadrato degli scarti, pesati, tra le yi e le f(xi;a) predette.
Questo metodo e’ noto come Metoto dei Minimi Quadrati.
Il metodo fornisce un mezzo per stimare il parametro a in una funzione f(xi; a) che fornisce i valori
veri di y per ogni x.
I dati usati sono le {xi} , assunte senza errori, ed i corrispondenti valori {yi} misurati con errore σi.
Si costruisce, per tutti i punti, la somma del quadrato delle differenze fra i valori misurati e quelli
attesi f(xi; a) opportunamente scalate di σi.
n
2
2
[ yi − f ( xi ; a )]2
Questa somma χ = ∑
e’ detta χ . Essa e’ la somma del quadrato di n variabili
2
1
σ
i
normali standardizzate.
Si vuole il valore di a che rende minima questa somma . Se sono note le derivate di f rispetto ad a il
problema e’ di trovare la soluzione:
2
n 1 df ( x ; a )
dχ
i
= 0; ∑ 2
[ yi − f ( xi ; a)] = 0 .
1 σ1
da
da
Se le σi = σ sono tutte eguali la soluzione si ha risolvendo la :
2
2
n
df ( xi ; a)
dχ
= 0; ∑
[ yi − f ( xi ; a )] = 0 .
1
da
da
Se non si conoscono gli errori σ , la soluzione per a si ottiene dalla stessa relazione usata per le σi =
σ =cost.
^
Il valore stimato di a , indicato con a , sara’ prossimo al valore vero ma non coincidera’ con esso.
^
^
La stima a e’ funzione delle yi : a = a ( yi ) . Usando la propagazione degli errori, assumendo le yi
indipendenti, si ottiene la varianza del valore stimato:
n
∂a
σ ^2 = ∑ ( ) 2 σ i2 .
a
∂yi
1
Se la f contiene N parametri { a1, a2, …, an}, essi si otterranno dalla soluzione di un sistema di N
equazioni in N incognite :
2
n
df ( xi ; ai )
dχ
= 0; ∑
[ yi − f ( xi ; ai )] = 0 ; i = 1 , …, N
1
dai
dai
Il caso della retta , della interpolazione lineare, e’ il piu’ comune: y = f(xi; a,b)= a + b x.
Supposte valide le condizioni descritte sopra e σi = σ = cost, la probabilita’ di ottenere un valore yi
per un dato xi e’ data da:
P ( yi ; a , b ) =
dyi
−
•e
n
∑
[ yi − f ( xi ; a )]2
2σ 2
.
2π
La probabilita’ di ottenere l’insieme completo di misure {yi} e’ il prodotto
σ
1
P = ∏1 P( yi ; a, b) = (∏1
n
−
dyi
n
)•e
σ 2π
n
∑
1
[ yi − ( a + bx )]2
2σ
2
=(
dyi
σ 2π
−
)n • e
n
∑
1
[ yi − ( a + bx )]2
2σ 2
.
La funzione di verosimiglianza e’ espressa come:
−
1
)•e
σ 2π
Il logaritmo di L vale:
L = (∏1
n
n
∑
1
[ yi − ( a + bx )]2
2σ
2
n
=(
l = ln L = ln ∏1 P( yi ; a, b) = ∑ ln[(
n
1
n
∑
[ yi − ( a + bx )]2
1
)n • e
σ 2π
−
1
[ yi − f ( xi ; a)]2
] = −n ln(σ
2σ 2
σ 2π
n
)n − ∑
1
1
2σ 2
1 n [ yi − ( a + bxi )]2
2π ) − ∑
2 1
σ2
Il Metodo di Massima Verosimiglianza consiste nel fare l’assunto, che la migliore stima di a e b ,
basata sulle n misure {yi} ottenute, e’ fornita dai valori degli stessi per cui L o l sono massime, e
questo equivale a minimizzare :
n
[ yi − (a + bxi )]2
.
χ2 = ∑
2
σ
1
(Il metodo e’ stato trattato in dettaglio nel corso di Lab. 1)
Esempio:
Vediamo come esempio il caso semplice in cui y e’ propozionale ad x : y = mx.
Questo e’ un semplice esempio di fit con m come unico parametro incognito. La quantita’ da
minimizzare in funzione di m, e’
n
[ yi − mxi ]2
χ2 = ∑
2
i =1
σ
i
Differenziando rispetto ad m si ottiene
3
[ y − mx ]
∂χ 2 n
= ∑ − 2 xi i 2 i
∂m i =1
σi
Se si assume che tutte le yi abbiano lo stesso errore σ
∂χ 2
2 n
2 n
= − 2 ∑ xi [ yi − mxi ] = − 2 ∑ ( xi yi − mxi2 )
∂m
σ i =1
σ i =1
Per la stima di m questa quantita’ e’ zero:
n
n
n
2 n
− 2 ∑ ( xi yi − mxi2 ) = 0; ∑ ( xi yi − mxi2 ); ∑ xi yi = m∑ xi2
σ
i =1
i =1
i =1
1=1
n
^
La stima di m diventa: m =
∑ xi yi
i =1
n
∑
.
2
i
x
1=1
La precisione di questa stima , applicando la propagazione degli errori, risulta
^
n
∂m
σ ^ = ∑ ( )2σ 2 = ∑ (
m
∂yi
1
1
2
n
xi
n
∑
1=1
)2σ 2 =
xi2
σ2
n
∑
1=1
; σ^ =
xi2
m
σ
n
∑
1=1
xi2
Proprieta’ degli stimatori .
Eseguita la misura di due grandezze fisiche (x,y) e riportati i valori (xi,yi±σi) su di un grafico
cartesiano, nasce il problema di stabilire quale sia la relazione funzionale, y = f(xi,a) piu’ adatta per
interpolare i dati. Le yi si assumono indipendenti e gaussiane.
Il metodo dei minimi quadrati ci permette di determinare una stima dei parametri ma non ci
fornisce indicazioni sulla scelta della funzione.
Nel caso di una retta, di una relazione lineare : y = a + bx, per valutare i parametri si rende minima
la somma
n
χ =∑
2
(Δy i ) 2
σ i2
1
n
=∑
( y i − a − bxi ) 2
n
= ∑ z i2 .
σ i2
1
1
Questo vale sia nel caso che le σi siano eguali, sia in quello in cui siano differenti per ciascuna delle
yi.
N
N
[ y − (a + bx)]2
(Δy i ) 2
=∑
Se le σi non sono note si stimano con: S y2 = ∑ i
N −2
1
1 N −2
Valutati a e b, nel caso di σi = σy =costante, si ottengono le loro incertezze attraverso le relazioni :
N
σ =
2
a
σ y2 ∑ xi
,σ =
2
b
1
n
N
N ∑ x − (∑ xi )
1
2
i
1
2
σ y2 N
n
N
1
1
N ∑ xi2 − (∑ xi ) 2
Finora la procedura e’ stata semplicemente una determinazione di parametri.
Per le stime, a e b, dei parametri valgono le seguenti proprieta’ :
• E[a + b x] = E[a] + x E[b] = A + B x.
I valori veri A e B sono stimati da a e b che si suppongono distribuiti normalmente, con varianze
σ a2 e σ b2 , attorno ai valori veri A e B. La varianza σ y2 si suppone nota.
a e b sono detti stimatori corretti di A e B.
4
σ a2 = E[(a – A)2] = minima. σ b2 = E[(b – B)2] = minima. Gli stimatori a e b sono stimatori
efficienti e precisi di A e B.
n
n
n
(Δy i ) 2
( y i − a − bxi ) 2
2
• χ =∑
=
=
z i2 segue la distribuzione χ2 con DF = n -2 .
∑
∑
2
2
σi
σi
1
1
1
2
Nel caso di n misure dirette {yi ± σ y } della grandezza Y,
•
1 n
∑ yi e’ la migliore stima del valore medio della popolazione da cui il
n 1
campione e’ ottenuto, che si assume come il valore vero della grandezza .
n
n
n
( Δy i ) 2
( yi − y) 2
2
la variabile : χ = ∑
=
=
z i2 segue la distribuzione χ2 con
∑
∑
2
2
• il valore medio y =
•
σy
σy
1
1
DF = n – 1 gradi di liberta’.
• σ y2 = E[(yi – y )2] = minimo. La media e’ uno stimatore efficiente o preciso.
1
• E[ y ] = μY. La media e’ uno stimatore corretto di Y.
Nel caso di n misure dirette {yi± σ i2 } della grandezza ,
n
• la media pesata y =
1
n
n
1
•
( Δy i ) 2
σ i2
n
=∑
1
2
i
1
∑σ
1
χ2 = ∑
yi
∑σ
e’ la migliore stima della grandezza , e la variabile :
2
i
( yi − y) 2
σ i2
n
= ∑ z i2 segue la distribuzione χ2 con DF = n – 1 gradi di
1
liberta’.
σ y2 = E[(yi – y )2] = minimo.
• E[ y ] = μY.
Se la distribuzione dell’errore non e’ nota la soluzione dei minimi quadrati gode ancora delle
proprieta’ :
• Le soluzioni sono senza bias , sono corrette;
• Fra tutte le soluzioni, che sono stime senza bias della grandezza e combinazioni lineari delle
misure yi, le soluzioni dei minimi quadrati hanno varianza minima;
n
n
(Δy i ) 2
( y i − a − bxi ) 2
• χ2 = M = ∑
,
E[M] = n – 2.
=
∑
2
2
1
σi
1
σi
TEST del χ2 : raccomandazioni per l’interpretazione e l’uso.
Prendendo come esempio il caso di andamento lineare, possiamo vedere quanto bene la curva si
adatta ai dati. Il test del χ2 permette di decidere se una relazione funzionale approssima
“statisticamente” i punti sperimentali, oppure scegliere tra piu’ relazioni funzionali quella che li
approssima meglio.
Come primo passo sempre fare e rappresentare il GRAFICO di confronto dei punti misurati con
la curva.
5
n
Note le σi, se le yi sono normali, allora χ = ∑
2
1
( Δy i ) 2
σ i2
n
=∑
( yi − y) 2
1
σ i2
n
= ∑ z i2 e’ una variabile χ2
1
con DF = n – 2 gradi di liberta’.
Valutato il χ2M , in funzione dei parametri a e b che lo minimizzano, si esegue il test del χ2.
• Se χ2Μ >> n -2 occorre controllare bene l’assunto sul quale si basa il calcolo.
• Nel caso χ2Μ ≤ DF =n −2 ,P[ χ2DF > χ2Μ] > α: la funzione e' corretta al livello di
significativita’ di α.
• Se χ2Μ eccede il valore critico del χ2, che corrisponde al livello di significativita’ α e
DF = n -2 ,si rigetta il risultato al livello di significativita’ di α.
Se P[ χ2DF > χ2Μ] < α : Rigetto.
Il rigetto puo’ essere causato da piu’ ragioni:
-da un errore di I specie;
-la y = f ( xi,a) non e’ corretta e non e’ a applicabile,o perche’ totalmente sbagliata o
qualche parametro di essa, che si e’ supposto noto, non e’ corretto.
• Se χ2Μ << DF = n -2 : o gli errori sono sovrastimati, o i dati sono stati selezionati in modo
speciale, o siamo stati fortunati a selezionare valori di yi molto prossimi a quelli attesi.
Se il test fallisce , ( sempre fare come primo passo il GRAFICO), perche’ si trovano modelli
migliori, in quanto ci sono evidenti deviazioni sistematiche dai punti della linea retta, si puo’
assumere una forma non lineare. Si possono nuovamente interpolare i dati, confrontandoli
col nuovo modello di regressione
ESEMPI
polynomial degree
1
polynomial degree
1
1.85563 x - 1.44361
2
1
0
0
-1
-1
0.2
0.4
0.6
2.73046 x - 0.894224
2
1
-2
0.0
1
0.8
1.0
Gli ultimi tre punti non sembrano piu’ appartenere alla retta.
-2
0.0
0.2
0.4
0.6
0.8
1.0
Il punto centrale devia di piu’ di 3 σ dalla retta.
6
0?21x
0.6
0.4
0.2
?2.0
polynomial degree
1
1
2.33807 x - 1.64244
2
1
0
-1
-2
0.0
I punti sembrano essere bene interpolati da una parabola
polynomial degree
0.2
2
polynomial degree
1.77587 x2 + 0.458199 x - 1.5923
1.0
2
0
0
-1
-1
0.4
0.6
2.7596 x2 - 0.279871 x - 1.5157
2
1
0.2
0.8
2
1
-2
0.0
0.6
mentre la retta non li interpola (successione di scarti tutti
positivi poi tutti negativi, poi nuovamente positivi)
2
2
0.4
0.8
-2
0.0
1.0
0.2
0.4
0.6
0.8
1.0
Gli ultimi tre punti non sembrano piu’ appartenere alla parabola. Ecco come cambia il fit escludendoli.
polynomial degree
polynomial degree
2
12.9256 x2 - 14.4205 x + 2.40084
2
1
0
0
-1
-1
0.2
0.4
0.6
- 8.1193 x3 + 25.7566 x2 - 19.8212 x + 2.86375
2
1
-2
0.0
3
0.8
1.0
-2
0.0
0.2
0.4
0.6
0.8
1.0
L’andamento parabolico non interpola sufficientemente bene i dati; quello cubico interpola bene .
7
polynomial degree
1
polynomial degree
2
- 0.27769 x2 + 3.63093 x - 1.45567
3.37832 x - 1.42167
2
2
1
1
0
0
-1
-1
-2
0.0
0.2
0.4
0.6
0.8
-2
0.0
1.0
0.2
0.4
0.6
0.8
1.0
Non ci sembrano motivi per rigettare l’interpolazione lineare e sceglierne una parabolica(figura di destra).
Se il test fallisce , ma non sembrano esistere modelli migliori, perche’ non si riscontrano deviazioni
sistematiche dalla linea retta, si devono rivedere le assunzioni fatte sugli errori. Essi possono
essere basati su stime troppo rozze o supposizioni non corrette, e possono essere sottostimati o
sovrastimati.
Infatti, riferendoci per semplicita’ al caso di σ y2 = cost., se la σ y e’ sottostimata di un fattore F, tutti
i termini della matrice degli errori ed il χ2
N
n
χ2 = ∑
1
( Δy i ) 2
σ y2
n
=∑
1
( y i − a − bxi ) 2
σ y2
, σ a2 =
σ y2 ∑ xi
, σ b2 =
1
n
N
N ∑ x − (∑ xi )
1
2
i
1
2
σ y2 N
n
N
N ∑ x − (∑ xi )
1
2
i
,
2
1
sono influenzati.
Le varianze σ a2 , σ b2 sono aumentate di F2, mentre il valore del χ2 e’ diminuito di F2.
σ a' = σ a • F ; σ b' = σ b • F ; χ '2 =
χ2
F2
La matrice degli errori e’ stata calcolata secondo l’errore sulle y. I valori dei parametri , pero’ non
vengono modificati poiche’ il punto di minimo del χ2 non dipende da σ y . Al contrario il valore del
minimo del χ2 ( che serve per il test) ed i valori della matrice degli errori sono molto influenzati dal
valore di σ y . Vedere esempio A.
Solo il test del χ2 ( non il valore degli errori sui parametri) indica quando il modello assunto nella
regressione , in questo caso una dipendenza lineare, e’ giustificato. Se σ y e’ piccolo , σ a e σ b sono
piccoli, ma il χ2 puo’ essere grande ed il test fallisce, anche se gli errori sui parametri sono piccoli.
E’ necessario ottenere una attendibile , anche se rozza stima di σ y per potere effettuare il test del
χ2.
Se le σ y non sono note ( misure fatte con lo stesso strumento, senza sistematici, errore ignoto) il
metodo da solo non permette di decidere quando il modello e’ giustificato.
Rimane il riscontro qualitativo, derivante dall’analisi critica del grafico y = y(xi,a), per la ricerca di
deviazioni sistematiche dei punti dalla linea ipotizzata . Se tali deviazioni sembrano esistere , allora
occorre costruire altre forme non lineari e confrontarle con i dati.
8
Per stabilire se per una serie di punti e’ giustificato l’uso di una interpolazione lineare, come gia’
visto in piu’ occasioni, si puo’ fare uso del coefficiente di correlazione lineare ρ.
Se le σ y non sono note , il metodo MMQ si puo’ sempre applicare . Si stimano i parametri a e b
(Δy i ) 2
.
col solito metodo. Gli errori sulle yi si assumono tutti eguali e sono stimati da S = ∑
n−2
1
Gli errori sui parametri si ottengono a partire da S y2 :
2
y
n
N
S a2 =
S y2 ∑ xi
1
n
N
1
1
N ∑ xi2 − (∑ xi ) 2
S b2 =
S y2 N
n
N
1
1
N ∑ xi2 − (∑ xi ) 2
Il test del χ2 pero’ non si puo’ effettuare.
n
n
S y2
( Δy i ) 2
( y i − a − bxi ) 2
La variabile per il test vale: χ 2 = ∑
n
=
=
(
−
2
)
∑1
σ y2
σ y2
σ y2
1
Se si assumesse σy = Sy allora il valore del χ2 assume il valore atteso χ2 = n - 2 =DF, e non avrebbe
piu’ alcun significato statistico.
La variabile per il test si puo’ scrivere , come appena visto,
~ 2
~ 2
S y2
S y2
χ2
2
=
.
χ = (n − 2) 2 ed il χ come χ =
n − 2 σ y2
σy
La varianza σy della popolazione e’ una caratteristica della dispersione dei dati dalla distribuzione
primaria : y = A + B x e non e’ indicativa della bonta’ del fit.
La Sy stimata, e’ invece caratteristica sia della dispersione dei dati sia dell’accuratezza del fit.
~ 2
S y2
La definizione di χ = 2 come rapporto della varianza stimata e la varianza della popolazione
σy
~ 2
rende il χ come una misura conveniente della bonta’ del fit.
Se la funzione fit fosse una buona approssimazione della funzione vera , allora la varianza stimata
~ 2
S dovrebbe accordarsi bene con la varianza σ ed il valore di χ dovrebbe assumere un valore
2
y
2
y
prossimo ad 1.
Se la funzione fit non e’ adatta per descrivere i dati, la deviazione sara’ piu’ grande e portera’ a
~ 2
~ 2
valori di χ > 1 o χ >> 1.
~ 2
Valori di χ < 1 non indicano, necessariamente, un miglioramento del fit, ma la conseguenza del
fatto che esiste una incertezza nella determinazione della variabile casuale S y2 , che fluttua, da
~ 2
~ 2
campione a campione, seguendo una distribuzione χ ;di conseguenza il valore del χ , in prove
ripetute, fluttua da esperimento ad esperimento.
E’ bene stimare sempre S y2 e confrontarlo con σ y2 (se nota).
Se il test fallisce , e si decide di rivalutare gli errori attraverso la S y2 , anche gli errori sulle stime
dei parametri devono essere rivalutati.
9
ESEMPIO A
Consideriamo la regressione lineare che fa uso delle stesse misure ma in cui si fanno tre differenti
assunzioni circa il loro errori.
Si esegue una regressione per una serie di dati , che sono riportati in tabella.
t
0.5
11.2
19.3
30.7
51.0
y
5.0
8.0
23.0
36.0
43.0
Si fanno tre differenti assunzioni circa le deviazioni standard delle misure y.
a) σy = 1;
b) σy = 8;
c) σy non nota.
I risultati sono riportati nelle figure e tabelle che seguono.
Per la regressione si assume la forma: y = a + b t.
La matrice di covarianza si esprime come:
N
⎞
⎛ N
− ∑ ti ⎟
2 ⎜ ∑ ti
2
2
N
N
⎛ σ a σ ab ⎞ σ y ⎜ 1
1
⎟; Δ = N t 2 − ( t ) 2 ,
⎜ 2
⎟
=
∑
∑
i
1
N
2 ⎟
⎜σ
⎟
1
1
⎝ ab σ b ⎠ Δ ⎜ − ∑ ti
N
⎟
⎜
⎠
⎝ 1
ed il valore del χ2 come:
n
n
S y2
( Δy i ) 2
( yi − a − bti ) 2
n
=
=
(
−
2
)
χ2 = ∑
∑1
σ y2
σ y2
σ y2
1
Il valore interpolato,Y, per un certo valore di t = T vale: Y = a + b T.
2
La varianza di Y vale: σ Y2 = σ a2 + T 2σ b2 + 2Tσ ab
.
Sebbene i parametri a e b non siano influenzati dalle assunzioni , vi e’ una significativa
influenza sulla matrice di covarianza, sul minimo del χ2 e sui limiti di confidenza.
• σy = 1. a = 4.35 ± 0.538
b= 0.827± 0.00067
J
0.538383
−0.0150125
N
−0.0150125 0.00066604
χ2= 90.42
I limiti di confidenza sono molto piccoli; gli errori sui parametri sono molto piccoli ,tuttavia
il valore del χ2 e’ grande cosicche’ il test fallisce ( DF =3; α = 0.01;χ2c = 11.340)
• σy = 8. a = 4.35 ± 34.45
b= 0.827± 0.0427
J
•
34.4565
− 0.960802
N
− 0.960802 0.0426265
χ2=1.41
I limiti di confidenza , gli errori sui parametri sono grandi ma il valore del χ2 e’ piccolo il fit
sembra ragionevole.
σy = incognita a = 4.35 ± 16.28
B = 0.827± 0.0201
16.2861
− 0.454129
J
N
− 0.454129 0.0201477
10
1 N
( yi − a − bti ) 2 ; Sy = 5.5
∑
N −1 1
I limiti di confidenza sono ragionevoli confrontati con le variazioni dei dati.
Il test del χ2 non puo’ essere valutato.
Sy e’ incognito ed e’ stimato da s y2 =
Nelle figure sono riportati, per le tre situazioni, i grafici che
confrontano i dati con la retta che meglio li interpola, i valori
dei parametri stimati e la matrice di covarianza, i limiti di
accettazione e rigetto , fissato α = 5% e 1%, per il test χ2.
σy = 1
40
30
20
J
10
10
20
30
40
50
4.35293
0.538383
−0.0150125
NJ
N
0.827288 −0.0150125 0.00066604
σy=8
50
40
30
20
10
10
20
30
40
50
J
34.4565
− 0.960802
4.35293
N
NJ
− 0.960802 0.0426265
0.827288
11
σy = incognito ; Sy = 5.4
40
30
20
10
J
10
20
30
40
50
c 2 0.95H3L = 0.352 and c 2 0.05H3L = 7.815
0.3
0.3
4.35293
16.2861
− 0.454129
NJ
N
− 0.454129 0.0201477
0.827288
c 2 0.99H3L = 0.115 and c 2 0.01H3L = 11.345
0.2
0.2
0.1
0.1
2
4
6
8
- 0.1
2
4
6
8
- 0.1
Ricerca della migliore forma funzionale.
Si supponga di avere 7 coppie di misure , i valori dei quali sono riportati in tabella.
yi ± 0.5 5.0 4.5 6.0 7.5 7.5 8.5 8.5
xi
2
3
4
5
6
7
8
Gli errori sulle Xi si ritengono trascurabili.
Si vuole determinare la migliore forma funzionale che lega le due grandezze.
Si prendono in esame due funzioni:
A) y = a + bx ;
B) y = k ln (x)
Col metodo dei minimi quadrati si determinano i valori dei parametri.
Nel caso della funzione A) si ottengono: a = 3.25 ± 0.51 , b = 0.714 ± 0.095
Nel caso della funzione B) si ottiene:
k = 4.364 ± 0.023.
In figura e’ riportato il confronto tra i dati sperimentali e le due curve “best fit”.
Il test del χ2 si puo’ utilizzare per decidere quale delle due funzioni si adatta meglio ai punti
sperimentali.
Per la curva A) il valore di ottenuto vale :χ2M = 6.6 , i gradi di liberta’ risultano :DF = 7 -2 = 5.
12
Il valore di χ ridotto =
χM 2
= 1.3 . La probabilita’ di ottenere un valore pari o maggiore di quello
DF
ottenuto vale P[ χ2DF > χ2M ] = 0.25.
Per la curva B) ) il valore di ottenuto vale :χ2M = 19 , i gradi di liberta’ risultano :DF = 7 -1 = 6.
2
c 2 0.95H6L = 1.635 and c 2 0.05 H6L = 12.592
0.3
0.2
0.2
0.1
0.1
5
10
c 2 0.95H5L = 1.145 and c 2 0.05H5L = 11.070
0.3
2
15
4
6
8
10
12
14
- 0.1
- 0.1
Il valore di χ 2 ridotto =
χM
2
= 3.1 . La probabilita’ di ottenere un valore pari o maggiore di quello
DF
ottenuto vale P[ χ2DF > χ2M ] = 0.005.
9
8
7
6
5
4
3
4
5
6
7
8
L’andamento lineare si adatta molto meglio ai dati sperimentali.
La coppia di valori (2. ; 5.0 ± 0.5) nel caso dell’andamento y = k ln(x) è quella che influenza
maggiormente il valore del χ2M , infatti la discrepanza tra valore misurato y1 =5.0 e valore atteso
k ln(2) = 3. è pari a 4 deviazioni standard.
Se si reputasse , per qualche motivo, di eludere questo valore si otterrebbero i nuovi valori :
Per la curva A) a = 2.72 ± 0.69 ; b = 0.79 ± 0.12
il valore di ottenuto vale :χ2M = 5.7 , i gradi di liberta’ risultano :DF = 6-2 = 4.
Il valore di χ 2 ridotto =
χM 2
= 1.4 . La probabilita’ di ottenere un valore pari o maggiore di quello
DF
ottenuto vale P[ χ2DF > χ2M ] = 0.22.
Per la curva B) k = 4.238 ± 0.029
il valore di ottenuto vale :χ2M = 2.5 , i gradi di liberta’ risultano :DF = 6 -1 = 5.
Il valore di χ 2 ridotto =
χM 2
= 0.5 . La probabilita’ di ottenere un valore pari o maggiore di
DF
quello ottenuto vale P[ χ2DF > χ2M ] = 0.75.
La figura mostra i nuovi andamenti.
13
9
8
7
6
5
4
5
6
7
8
L’esclusione della prima coppia di valori, non cambia in modo apprezzabile i valori dei parametri,
ma fa si che questa volta l’andamento logaritmico sembri piu’ adatto a descrivere i dati
sperimentali.
Il rigettare o meno la prima coppia di valori è cruciale per interpretare i dati.
Occorre cautela ed un’analisi accurata degli eventuali sistematici, e se l’analisi non dovesse risultare
decisiva, occorre ripetere la misura.
Appendice:determinazione, mediante il MMQ, di k .
y = k ln(x): determinazione di k ±σk col metodo dei minimi quadrati. Si suppone σyi = σ = cost
n
( y − k ln( xi )) 2
χ2 = ∑ i
2
σ
1
∂χ
2
= − 2 ∑ ( yi − k ln xi ) ln xi = 0
σ 1
∂k
2
n
n
n
∑ ( y ln x ) = −k ∑
i
i
1
(ln xi ) 2
1
n
k=
∑ y (ln x )
i
1
n
∑
i
(ln xi ) 2
1
La varianza di k si ottiene propagando gli errori sulle yi
2
σ k2
n
⎞
⎛
σ 2 ∑ (ln x j ) 2
⎟
⎜
n
n
ln x j ⎟ 2
∂k 2 2
) σ = ∑⎜ n
σ = n j =1
=
= ∑(
⎟
⎜
∂y j
2 2
2
j =1
1
[∑ (ln xi ) ]
⎜ ∑ (ln xi ) ⎟
i =1
⎠
⎝ i =1
σ2
n
∑ (ln x )
i =1
2
i
n
k=
∑ y (ln x )
i
1
n
∑
1
σ
i
(ln xi ) 2
±
n
∑ (ln x )
i =1
2
i
14
Esempio.
Si interpolino , con il MMQ , N = 20 punti ( xi,yi)
- Interpolazione lineare : DF = N- 2 = 20 – 2 = 18. Sia χ2M= 36.3 il valore ottenuto.
P[ χ218 > 36.3] = 1%
- Parabola: DF = N- 3 = 20 – 3 = 17. Sia χ2M= 20.1 il valore ottenuto.
P[ χ217 > 20.1] > 20%
- Cubica: DF = N- 4 = 20 – 4 = 16. Sia χ2M= 17.6 il valore ottenuto.
P[ χ216 > 17.6] > 20%
E’ improbabile, nel caso della retta, che per fluttuazioni casuali si ottenga un valore di
χ2M= 36.3: la probabilita’ P[ χ218 > 36.3] dell’ 1% e’ moto piccola. La retta e’ improbabile. H0 e’
scartata al livello di significativita’ dell’1%. Rigetto altamente significativo.
Per la relazione parabolica la P[ χ216 > 17.6] > 20% e’ elevata, in diversi campionamenti una volta
su 5 possiamo trovare un valore grande come quello ottenuto. Se rigettiamo l’ipotesi di accordo
incorriamo in un errore di I specie con una probabilita’ del 20 %. Non abbiamo motivo di dubitare,
al livello di fiducia del 5 %, dell’accordo tra parabola e dati. Le fluttuazioni sono dovute al caso.
Non c’e giustificazione per la relazione cubica.
Errori su x non trascurabili: ancora qualche raccomandazione.
Nel MMQ gli errori sulle ordinate sono assunti nulli, e tutta la incertezza e’ associata alla variabile
dipendente y. Questo equivale ad assumere che la precisione delle x e’ considerevolmente piu’ alta
di quella sulle y.
Questa condizione puo’ essere considerata valida solo se le incertezze della yi, che possono essere
indotte da variazioni della xi prodotte da errori casuali nella misura della xi stessa, sono molto piu’
piccole delle incertezze della yi stessa. Questo e’ equivalente , in prima approssimazione, alla
richiesta, che per ogni punto misurato:
dy
σ x | |<< σ y
dove dy/dx e’ la pendenza della curva y = y(x).
dx
Se le incertezze indotte dalla x non sono trascurabili, la procedura di fit sara’ ancora
dy
sufficientemente accurata se stimiamo il contributo σ yI = σ x | | , e combiniamo, in quadratura,
dx
questo contributo con quello diretto σ yD , che e’ l’incertezza di misura di y:
2
σ y2 = σ yI2 + σ yD
Con questa assunzione, l’incertezza nei dati si associa solo alla variabile y dipendente, mentre le
corrispondenti fluttuazioni possono avere origine sia dall’incertezza sulle x sia da quella sulle y.
In quei casi dove l’incertezza nella determinazione della quantita’ indipendente sono
considerevolmente piu’ grandi di quelle sulla quantita’ dipendente, e’ piu’ opportuno scambiare i
ruoli delle due quantita’.
15
FIT POLINOMIO DI ORDINE m.
y = a0 + a1 x + a2 x 2 + ... + am x m
Per l’esecuzione del calcolo degli elementi delle matrici e’ opportuno usare un metodo che
semplifica la procedura e la riconduce a operazioni di prodotto di matrici, inversione e trasposizione
di matrici.
1 K 1 ⎞
⎛ 1
⎟
⎜
⎜ x1 x2 K xn ⎟
xi: i=1,…,n valori variabile x; m=grado del polinomio
H =⎜
M
M
M ⎟
⎟
⎜ m
m
m⎟
⎜x
x
L
x
n ⎠
2
⎝ 1
⎛1 x1
⎜
⎜1 x 2
T
H =⎜
⎜M M
⎜1 x
n
⎝
⎛ 1 2
⎜ σ1
⎜
⎜ 0
C =⎜
⎜ M
⎜⎜ 0
⎝
K x1m ⎞
⎟
K x2m ⎟
M ⎟⎟
L xnm ⎟⎠
0
1
σ 22
L
matrice trasposta
0 ⎞⎟
⎟
⎟
⎟
⎟
1 2⎟
σ n ⎟⎠
σi2: varianza del valore yi; i=1,…,n
D = H ⋅C ⋅ H T
D −1 = ( H ⋅ C ⋅ H T )
−1
16
⎛ y1 ⎞
⎜ ⎟
⎜y ⎟
Inoltre, indicando con: Y = ⎜ 2 ⎟ e con: B = H ⋅ C ⋅ Y
M
⎜ ⎟
⎜y ⎟
⎝ n⎠
−1
A= D B
A = ( H ⋅ C ⋅ H T ) −1 ( H ⋅ C ⋅ Y )
si ottiene:
⎛ a0 ⎞
⎜ ⎟
⎜a ⎟
A=⎜ 1 ⎟
M
⎜ ⎟
⎜a ⎟
⎝ m⎠
Esempio:
yi = a0 + a1 x + a2 x 2 ; ( xi , yi ± σ i ) ; i=1,…,n
⎛1
⎜
H = ⎜ x1
⎜ x2
⎝ 1
1
x2
x22
⎛1 x1
⎜
L 1⎞
⎟
⎜1 x 2
T
L xn ⎟ H = ⎜
⎜M M
L xn2 ⎟⎠
⎜1 x
n
⎝
⎛
⎜
x12 ⎞
⎟
⎜
x22 ⎟
⎜
C =⎜
⎟
M ⎟
⎜
xn2 ⎟⎠
⎜⎜
⎝
1
σ 12
0
M
0
0
L
1
σ 22
0
L
0 ⎞⎟
⎛ y1 ⎞
⎜ ⎟
⎟
0 ⎟
⎜ y2 ⎟
=
Y
⎜ M ⎟
⎟
M ⎟
⎜ ⎟
⎜y ⎟
1 2⎟
⎝ n⎠
⎟
σn ⎠
ESEMPI di interpolazione degli stessi dati con polinomi di ordine successivo.
17
T@sD
PRIMA PARABOLA ToHdL
2.3
2.2
2.1
2
T@sD
400
600
800
600
800
1000
SECONDA PARABOLA To'HdL
1200
d@mm D
2.1
2.08
2.06
2.04
2.02
400
1000
1200
d@mmD
1.98
18
T@ sD
PRIMA CUBICA ToHdL
2.3
2.2
2.1
400
T @sD
600
800
1000
1200
d@mm D
SECONDA CUBICA To'HdL
2.3
2.2
2.1
400
600
800
1000
1200
d@mmD
19
T@s D
PRIMA QUARTICA ToHdL
2.3
2.2
2.1
2
0
T@sD
SECONDA QUARTICA To'HdL
400
600
800
1000
1200
1400
d @mmD
2.15
2.1
2.05
2
0
400
600
800
1000
1200
1400
d@mmD
20
T@sD
CURVA DI QUINTO GRADO To
2.6
2.4
2.2
2
0
400
600
800
1000
1200
1400
d@ mmD
21
TEST χ2:Accordo tra una distribuzione teorica ed una sperimentale.
Con il test normale e di Student, abbiamo costruito dei test di ipotesi che specificano i valori di uno
o piu’ parametri della popolazione. Essi si possono indicare come test parametrici. La procedura
consiste nel rigetto o accettazione di una ipotesi sulla base sulla base di un singolo numero
determinato dal campione. Un’altra classe di test confronta la funzione di distribuzione del
campione direttamente con la distribuzione della popolazione ; quest’ultima puo’ essere basata su
alcune ipotesi.
Si vuole stabilire se vi e’ accordo tra una distribuzione teorica ed una sperimentale, se l’istogramma
delle frequenze sperimentali e’ compatibile con una distribuzione limite attesa , ottenibile solo nel
caso di un numero infinito di misurazioni.
Negli esempi in figura sono riportati i casi in cui la distribuzione limite attesa sia gaussiana,
uniforme ed esponenziale. In tutti e tre i casi ci si aspetta che all’aumentare del numero di prove ,
all’aumentare della grandezza del campione, la distribuzione sperimentale approssimi sempre
meglio quella attesa. Sono mostrate le fluttuazioni statistiche possibili in campioni di grandezza
N=100, e come esse diminuiscano all’aumentare della grandezza del campione N=1000 e
N=100000 .
Se si dispone di campioni di grandezza finita ad esempio N = 100, come si puo’ stabilire se le
fluttuazioni tra campione e campione e tra istogramma e distribuzione limite ipotizzata siano solo
casuali?.
Il test del χ2 puo essere utilizzato per rispondere alla domanda.
GAUSSIANA
100 values
100 values
-4
-2
0
2
4
-4
-2
0
2
4
100 000 values
1000 values
-4
-2
0
2
4
-4
-2
0
2
4
22
UNIFORME
100 values
100 values
0
0.2
0.4
0.6
0.8
0
1
0.2
0.4
0.6
0.8
1
1000 values
100 000 values
0
0.2
0.4
0.6
0.8
1
0
0.2
0.4
0.6
0.8
1
ESPONENZIALE
100 values
100 values
0
2
4
6
8
0
2
4
1000 values
0
2
4
6
8
100 000 values
6
8
0
2
4
6
8
Si abbia una variabile casuale x. Si disponga di n dati sperimentali xi.
Si divida l’intervallo delle eventualita’ di x in k classi tra loro mutuamente esclusive e di ampiezza
Δx. Sia pi la probabilita’ che un valore di x cada nella classe i-esima.
Si indichino con Oi le frequenze sperimentali osservate,ossia il numero di volte che si sono
presentati i valori di x in tale classe (intervallo). Se Oi rappresenta la frequenza assoluta in quella
23
classe, νi = Oi/n rappresenta la frequenza relativa. Si costruisca l’istogramma delle frequenze
sperimentali.
Si indichino con Ei le frequenze assolute teoriche attese : Ei = n pi. La frequenza relativa teorica
attesa coincide con pi .
La
k
k
1
1
∑ Oi = n ; ∑ pi = 1
Se le variabile x e’ discreta Ej = n pj
Se la variabile x e’ continua e f(x) e’ la funzione densita’ di probabilita’,
le probabilita’ per valori di x di appartenere alla classe j sono: p j = ∫
xj + Δx
xj
f ( x)dx ≅ f ( x*j ) • Δx
dove f ( x*j ) e’ calcolato nel valore centrale della classe j. Il numero atteso di valori nella classe j
vale : Ej = n pj.
La distribuzione congiunta delle frequenze in prove ripetute ed indipendenti e’ multinomiale:
n!
P(O1 , O2 ,..., Ok ) =
( P1 ) O1 ( P2 ) O2 ...( Pk ) Ok .
O1!O2 !,..., Ok !
Le deviazioni standard valgono : σ i = npi qi , e se: pi <<1 allora σ i = npi = Ei . In ogni classe la
distribuzione delle frequenze Oi si puo’ assumere segua la distribuzione di Poisson di valore medio
Ei e varianza σ i2 = Ei .
Si usano le frequenze assolute Ei come frequenze vere , come norma, in ogni classe.
La quantita’ ( Oi – Ei)2 si puo’ ragionevolmente assumere come una misura della deviazione delle
frequenze teoriche Ei dalle sperimentali Oi.
Si debbono confrontare tra di loro le deviazioni dalla norma delle varie classi, ed e’ necessario
normalizzare tra di loro gli scarti.
(O − Ei ) 2
Consideriamo come scala, come misura di ogni deviazione il rapporto i
.
Ei
(Oi − Ei ) 2
, lo possiamo considerare come una misura della deviazione
Ei
1
totale. Sostituendo e sviluppando il quadrato si ottiene
k
k
k
k
k
O 2 + Ei2 − 2Oi Ei
O2 k
O2
(Oi − Ei ) 2
χ '2 = ∑
=∑ i
= ∑ i + ∑ Ei − 2∑ Oi = ∑ i − n .
Ei
Ei
1
1
1 Ei
1
1
1 Ei
k
Allora il valore χ ' 2 = ∑
k
Se consideriamo le frequenze assolute vale inoltre la relazione:
k
∑ E = ∑O
i
1
i
=n.
1
La variabile χ ' 2 e’ distribuita asintoticamente come una variabile χ 2 con DF = (k – 1 )gradi di
liberta’. Infatti , a causa del vincolo:
k
k
1
1
∑ Ei = ∑ Oi = n , solamente (k – 1 ) variabili Oi sono
realmente indipendenti.
Se non si stimano parametri della distribuzione teorica ipotizzata f(x) i gradi di liberta’ restano
( k-1).
Se si devono stimare h parametri della distribuzione , i gradi di liberta’ si riducono di numero :
DF = k – 1 – h, poiche’ si impongono (h + 1) vincoli sui dati.
Affinche’ la distribuzione χ ' 2 sia approssimata da quella χ 2 assume importanza il valore della
frequenza assoluta attesa Ei in ogni classe.
Esse debbono essere in ogni classe : Ei = n pi > 5. Questo potra’ venire realizzato con opportuni
raggruppamenti di classi.
24
Se si assume che la variabile i-ma si comporti approssimativamente come una variabile di Poisson
(O − Ei ) 2
di valore medio μ = Ei e varianza σ2 = Ei allora il rapporto i
rappresenta il quadrato di
Ei
una variabile standardizzata di Poisson. Per μ > 5 una variabile di Poisson puo’ gia’ essere ben
k
(Oi − Ei ) 2
2
approssimata da una variabile gaussiana, e la sommatoria: ∑
= χ DF
= ∑ zi2 , risulta la
Ei
1
somma del quadrato di k variabili normali centrate e ridotte , ossia una variabile χ2 con
DF = ( k-1-h) gradi di liberta’.
Calcolato il valore χ '2 per applicare il test del χ 2 si deve decidere prima sul valore del livello di
fiducia e in base a questo si determinano i limiti della regione critica χα2 tale che
∞
2
P ( χ DF
> χα2 ) = α = ∫ 2 f DF ( χ 2 )dχ 2 (Uso tabelle).
χa
Le successive decisioni sono fissate avendo scelto la regione di accettabilita’ dell’ipotesi H0.
Se il valore χ M2 calcolato cade al di fuori della regione di fiducia ( χ M2 > χα2 ), nella zona di rigetto,
allora la distribuzione teorica non si adatta bene ai nostri dati al livello di fiducia di α.
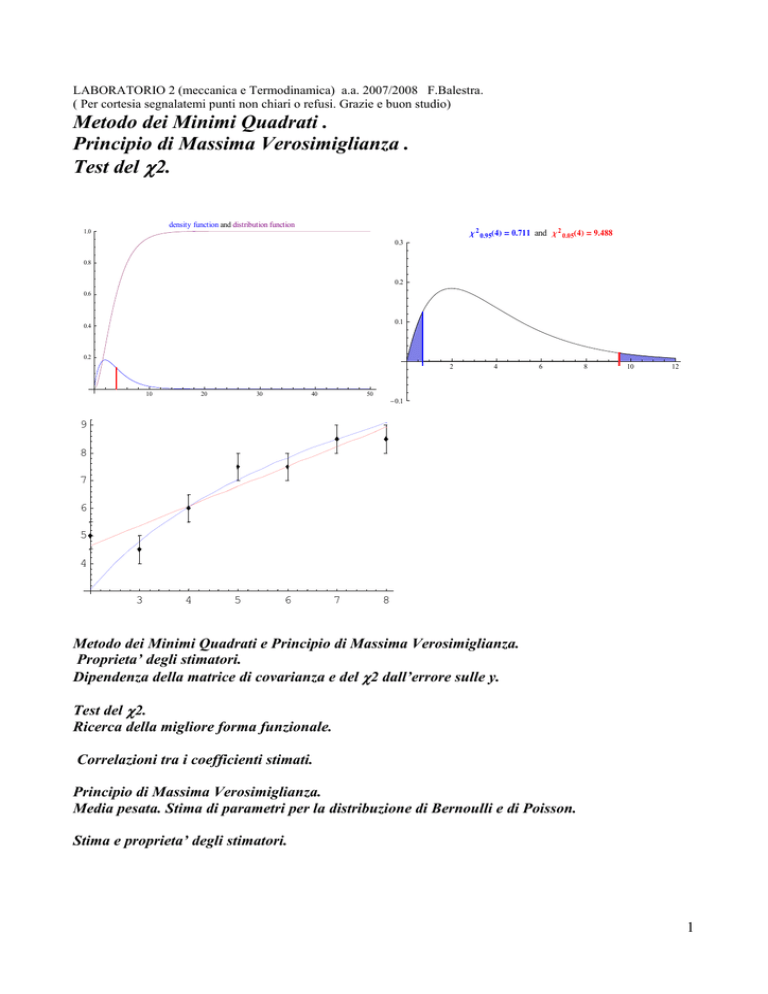
c 2 0.95H4L = 0.711 and c 2 0.05H4L = 9.488
0.3
0.2
0.1
2
4
6
8
10
12
- 0.1
Considerazioni
La distribuzione limite teorica (Ei) ci dice quanti eventi di un certo tipo sono attesi in una certa
classe quando il numero delle prove n e’ molto grande (n → ∞).
Ei = n pi: numero medio di conteggi attesi nella classe i.
In pratica, se ripetessimo la prova molte volte (se ricavassimo molti campioni di grandezza n) il
numero Oi osservato di eventi in ogni classe fluttuerebbe da una prova all’altra: Oi segue
25
approssimativamente una distribuzione di Poisson. I diversi valori Oi dovrebbero avere valori medi
μ=Ei e dovrebbero fluttuare intorno ad Ei con σ=√Ei (errore statistico).
Cosi’ i numeri da confrontare sono le deviazioni (Oi - Ei) e σ=√Ei. Pertanto la quantita’:
(Oi − Ei ) 2
Ei
per alcuni dei k intervalli potra’ essere >>1, per altri <<1, in media ≈1.
χ
χ2
χ2
χ2
(Oi − Ei ) 2
e’ indice dell’accordo:
=∑
Ei
1
= 0: accordo perfetto (molto improbabile);
≤ D.F.: accordo;
>> D.F.: vi e’ il sospetto che la misura si discosti dal valore atteso.
2
k
(Oi − Ei ) 2
e’ la variabile standardizzata al quadrato. Gli intervalli dovrebbero essere scelti in modo
Ei
che il conteggio atteso Ei in una classe sia ragionevolmente grande (>5). Se i numeri in gioco sono
ragionevolmente grandi la distribuzione di Poisson e’ ben rappresentata dalla distribuzione normale,
quindi i numeri Oi possono essere trattati come fossero variabili casuali continue, distribuiti attorno
al valore medio Ei secondo la gaussiana, anche se nei problemi considerati Oi e’ una variabile
discreta distribuita secondo Poisson.
k
Allora χ '2 = ∑ (variabile normale standardizzata)2 puo’ essere pensata come una variabile χ2 e
i =1
seguire la fDF(χ2) distribuzione χ2 con gradi di liberta’ DF=k-h-1 (nel caso di una gaussiana in cui
sono stimati 2 parametri μ e σ, occorre che k≥4)
La condizione per cui Oi segua Poisson e’: pi<<1. Bisogna quindi impostare un numero opportuno
di classi perche’ essa sia verificata.
Occorre sottolineare, nel caso di una variabile continua, che il confronto tra le frequenze
sperimentali, variabili discrete, e le frequenze teoriche, variabili continue, e’ tanto piu’ attendibile
quanto piu’ n e’ grande e l’ampiezza della classe Δx e’ piccola.
(fare riferimento anche agli esempi gia’ trattati in Lab. 1)
26
TEST χ2 : Esempio per una distribuzione di Poisson
Rutherford e Geiger in una celebre esperienza studiarono le emissioni di particelle a da un preparato
radioattivo . Divisero il tempo in N = 2608 intervalli uguali aventi la durata di Δt = 7.5 s ciascuno, e
misurarono il numero Xi di particelle emesse in ogni intervallo. Ottennero i risultati dalle prime
due colonne della Tab 1. dove: Oi è il numero di intervalli in cui furono emesse Xi particelle.
Ei: rappresenta il numero di intervalli in cui ci si aspetta siano emesse Xi particelle se la
distribuzione e’ quella di Poisson con valore medio μ = x
Xi Oi
0 57
1 203
2 383
3 525
4 532
5 408
6 273
7 139
8 45
9 27
≥10
νi P(Xi) (Oi -Ei)2/E
Ei
54 0,022
211 0.078
407 0.147
525 0.201
508 0.204
394 0.156
254 0.105
140 0.533
68 0.017
29 0.010
0,021
0.081
0.156
0.201
0.194
0.151
0.097
0.054
0.026
0.011
600
0.11
0.298
1.52
0.0
1.1
0.55
1.5
0.01
7.60
0.14
500
400
Serie1
300
Serie2
200
100
0
0
1
2
3
4
5
6
7
8
9 10
La figura riporta l’andamento delle frequenze Oi ed Ei
L’accordo e’ buono.
Un criterio per valutare l’accordo e’ il test del χ2
TEST χ2 . Ipotesi nulla H0 : la distribuzione e’ poissoniana.
Stimiamo i valori attesi Ei= P(Xi)●N secondo tale ipotesi.
10
μ = x=
∑ xi Oi
0
10
∑O
10
=3.87 ; S 2 =
∑
(xi − x)
0
N − 1
2
= 3.63.
i
0
La teoria richiede s2 = μ : l’accordo e’ buono
μ xi • e − μ 3.87 xi • e −3.87
νi = Oi / N ; P ( xi ) =
=
xi !
xi !
Ei = N ●P(Xi) ; N= ∑Oi = 2608 ( 1 vincolo). Stimato il parametro μ ( secondo vincolo) . Numero
classi = 11.
I valori di P(Xi) e di Ei sono indicati in tabella. Indicare gli errori statistici sull’istogramma delle
frequenze.
Il valore del χ2M = ∑ (Oi-Ei)2/Ei = 11.3. I gradi di liberta’sono: DF=(11-2)=9. Il valore di
χ2M ridotto = χ2M / DF = 1. 2
P(χ2DF=9 ≥χ2M) = 29%. L’ipotesi di distribuzione poissoniana e’ accettata al livello di
significativita’ del 29%.
27
I valori di χ2 critici per D.F.= 9 sono , fissato un livello di fiducia del 5%, :limite a sinistra=3.33
limite destro= 16.92.
Il valore di χ2M = 11.3 cade entro tali limiti. L’ipotesi Ho si ritiene accettata.
Esempio
Si ottenga un campione di n = 120 lanci di un dado, che si suppone, non truccato.
Nel caso di un dado non truccato, le probabilita’ che si presentino le facce 1,2,3,4,5,6 sono tutte
eguali: p1=p2=p3=p4=p5=p6=1/6 .
Le corrispondenti frequenze assolute attese Ei sono:
np1 = np2 = …= np6= 120 (1/6) = 20.
Le frequenze realmente osservate Oi potranno essere diverse.
i
Oi
Ei = n pi
Oi - Ei
(Oi-Ei)2
1
22
20
2
4
2
11
20
-9
81
3
10
20
-10
100
4
17
20
-3
9
5
35
20
15
225
6
25
20
5
25
Si vuole controllare l’accordo tra l’andamento delle frequenze osservate Oi e l’andamento della
distribuzione di quelle teoriche attese, che si postula sia costante e pari a Ei = 20.
Se l’accordo non fosse buono, l’ipotesi di dado non truccato potrebbe non essere vera.
k
k
(Oi − npi ) 2
(Oi − Ei ) 2
'2
Si costruisce la variabile χ = ∑
.
=∑
npi
Ei
1
1
(Oi − npi ) 2
= zi si puo’ supporre
In ogni classe il valore atteso Ei = n pi e’ Ei > 5 , e la variabile
npi
(Oi − npi ) 2
segue una distribuzione
una variabile normale centrata e ridotta. La variabile χ = ∑
npi
1
χ2 con DF = k -1 gradi di liberta’. Le probabilita’ pi = 1/6 si suppongono note, e quindi non si
k
'2
k
debbono stimare parametri . Esiste un vincolo, poiche’
∑O
i
= n , e le variabili realmente
1
indipendenti non sono k ma (k -1). In questo caso il numero di variabili e k =6 e DF = 6 -1 = 5.
6
6
(Oi − Ei ) 2
(Oi − 20) 2 444
=∑
=
= 22.2
Il valore di χ2M vale χ M2 = ∑
20
20
Ei
1
1
Se si fissa un livello di fiducia α = 5% , per un valore DF =5 , il valore critico risulta χ2c = 11.07.
Il valore di χ2M osservato supera il valore critico al livello di significativita’ del 5 %.
Si scarta l’ipotesi che le probabilita’ siano eguali e pari a pi = 1/6, e che Ei =n pi = 20.
Le frequenze osservate differiscono in maniera significativa da quelle attese e si rigetta l’ipotesi che
ci sia accordo tra i valori di frequenza misurati e la forma ipotizzata , che prevede Ei = npi = 20.
La discrepanza tra valori osservati e quelli attesi non puo’ essere imputata solamente a fluttuazioni
casuali , l’ipotesi che il dado non sia truccato viene rigettata al livello di significativita’ del 5%.
Se α = 1% e DF = 5 il valore di χ2c risulta χ2c = 15. L’ipotesi che il dado non sia truccato puo’
venire rigettata anche al livello di significativita’ del 1%. Il rigetto e’ altamente significativo, si
puo’ commettere un errore di I tipo con probabilita’ inferiore all’ 1%.
28
c 2 0.95H5L = 1.145 and c 2 0.05H5L = 11.070
0.3
c 2 0.99H5L = 0.554 and c 2 0.01H5L = 15.086
0.3
0.2
0.2
0.1
0.1
2
4
6
8
10
12
2
14
4
6
8
10
12
14
- 0.1
- 0.1
Appendice 2:Esempio del significato delle correlazioni tra i coefficienti stimati col MMQ.
2.05
2.025
-1
-0.5
0.5
1
1.975
1.95
1.925
Fig 1:andamento del periodo attorno al coltello O in funzione del tempo. I punti sono interpolati,
previa traslazione dell’asse delle ascisse nel baricentro dei valori di , con una parabola (vedi
programma di Mathematica)
2.02
-1
-0.5
0.5
1
1.98
1.96
1.94
Fig2:andamento del periodo attorno al coltello O1 in funzione del tempo. I punti sono interpolati,
previa traslazione dell’asse delle ascisse nel baricentro dei valori di , con una parabola (vedi
programma di Mathematica)
29
2.05
2.025
-1
-0.5
0.5
1
1.975
1.95
1.925
Fig 3: calcolo del valore del periodo in corrispondenza dell’intersezione delle due parabole
2.02
-1
-0.5
0.5
1
1.98
1.96
1.94
1.92
1.9
scatter
ab
scatter
ac
0.02
0.12
0.015
0.11
0.01
0.005
1.895
1.905
1.91
1.915
0.09
1.895
1.905
scatter
1.91
1.915
bc
0.12
0.11
0.005
0.01
0.015
0.02
0.09
30
60
50
40
30
20
10
1.895
1.9
0
0.005
1.905
1.91
1.915
50
40
30
20
10
0.01
0.015
0.02
60
40
20
0.09
0.1
0.11
0.12
Fig 4: correlazione tra i coefficienti dei parametri di una parabola T=A+ Bd+Cd2 ottenuti col
metodo dei minimi quadrati. La figura riporta il coefficiente di correlazione (covarianza) tra i
parametri A-B, A-C, B-C. Come si nota i coefficienti di correlazione A-B e B-C sono fra di loro
scorrelati, infatti il diagramma mostra un coefficiente di correlazione prossimo a 0 . I coefficienti A
e C sono invece correlati come mostrato dal diagramma che indica una correlazione diversa da 0 e
negativa. La correlazione pari a 0 tra i coefficienti A e B e tra i coefficienti B e C è ottenuta grazie
alla traslazione dell’asse delle ascisse nel baricentro delle di.
Presa la serie di punti T(di )± σ i e interpolandoli si ottiene una parabola di coefficienti Ai, Bi, Ci.
Facendo variare ogni valore di entro l’errore σ i secondo, una distribuzione gaussiana, si ottiene
un’altra serie di dati che interpolati forniscono altri coefficienti Ai, Bi, Ci. Il procedimento si ripete
N volte ottenendo una serie del valore degli stessi con i=1…N. Negli istogrammi sono riportati le
distribuzioni ottenute dei valori dei coefficienti A, B ,C.
I diagrammi riportati sopra si ottengono mettendo in correlazione i vari coefficienti ottenuti.
31
Rapporto di verosimiglianza. Principio di massima verosimiglianza.
Si supponga che f(x, λ) sia una funzione densita’ di probabilita’ caratterizzata da k parametri (λ1, λ2,
…, λn). Sia x1, x2, …, xn un provino ottenuto da n misurazioni di una data grandezza fisica, il cui
comportamento e’ assimilabile a quello della variabile casuale x.
L’espressione dPj = f ( x j , λ )dx j e’ la probabilita’ di ottenere il valore x compreso tra xj e xj+dxj.
Se gli n risultati xj si suppongono indipendenti, allora la probabilita’ che x1 sia compreso tra x1 e
x1+dx1, x2 tra x2 e x2+dx2, …, e’ data dal valore della probabilita’ congiunta:
n
dP = ∏ f ( x j , λ )dx j
funzione di k parametri
j =1
n
L’espressione produttoria: L = ∏ f ( x j , λ ) e’ detta funzione di verosimiglianza. Essa non deve
j =1
essere identificata con una funzione densita’ di probabilita’ in senso stretto, anche se ne ha le
caratteristiche. Il termine “verosimiglianza” indica che essa ha il significato di una funzione densita’
di probabilita’ non a priori ma a posteriori, essendo definita sul provino di dati a disposizione.
Si supponga, per semplicita’, che la popolazione sia caratterizzata da un solo parametro che puo’
assumere al piu’ due valori λ1 e λ2, distinti tra loro. Si puo’ costruire il rapporto:
n
∏ f (x ,λ )
j
Q=
1
j =1
n
∏ f (x ,λ )
j
rapporto di verosimiglianza
2
j =1
Esempio: λ=parita’ di uno stato; λ1=dispari; λ2=pari
Il risultato del processo di campionamento puo’ indicare che l’insieme col parametro λ=λ1 e’ Q
volte piu’ probabile dell’insieme allorche’ λ=λ2.
Esempio: viene lanciata una moneta asimmetrica.
5 lanci: 1 volta T; 4 volte C
Tre ipotesi: A – PT=1/3; PC=2/3
B – PT=2/3; PC=1/3
C – PT=1/2; PC=1/2
A seguito dei risultati dell’esperimento, la funzione di verosimiglianza ha valore:
1⎛ 2⎞
ipotesi A → L A = ⎜ ⎟
3⎝ 3⎠
4
2⎛1⎞
ipotesi B → LB = ⎜ ⎟
3⎝ 3⎠
4
4
1⎛1⎞
ipotesi C → LC = ⎜ ⎟
2⎝2⎠
e dunque i rapporti di verosimiglianza risultano:
Q AB = LA LB = 8 Q AC = LA LC = 2.1 QBC = LB LC = 1.8
La verosimiglianza dell’ipotesi A e’ la piu’ alta fra tutte; e’ molto probabile che la moneta
appartenga alla classe A piuttosto che alla classe B o C.
Esempio: π1=0.4 e π2=0.2 rappresentino la proporzione di individui di gruppo sanguigno Rh- in due
diverse popolazioni. Si considerino le popolazioni bernoulliane e si osservi un campione di 20
individui: x=6 soggetti presentano questa caratteristica.
32
Ipotesi 1 → il campione proviene dalla popolazione π1
x
L( x, π 1 ) = π 1 (1 − π 1 ) n − x = 0.4 6 0.614 = 0.0000032
Ipotesi 2 → il campione proviene dalla popolazione π2
x
L( x, π 2 ) = π 2 (1 − π 2 ) n − x = 0.2 6 0.814 = 0.0000028
L ( x, π 2 )
= 0.875
Q=
L ( x, π 1 )
La verosimiglianza dell’ipotesi riferita alla popolazione π2=0.2 e’ del 12.5% piu’ bassa.
La funzione di verosimiglianza e di massima verosimiglianza.
Stima di parametri.
n
La funzione di verosimiglianza L = ∏ f ( x j , λ ) considerata come funzione di λ puo’ presentare uno
j =1
o piu’ massimi.
1) Un solo massimo λ1 con simmetria attorno a λ1: in tal caso
λ1 e’ la miglior stima di λ e la σ λ21 puo’ essere presa
come errore sulla stima di λ1.
2) Un solo massimo λ1 con asimmetria attorno a λ1: in tal caso
λ1 e’ la miglior stima di λ ma la σ λ21 e’ poco significativa.
Presentare L(λ) e λ1.
3) Piu’ massimi: e’ preferibile scegliere il λ che corrisponde
al massimo dei massimi di L(λ). Riportare L(λ).
Determinazione del massimo
La ricerca del massimo di L(λ) viene fatta risolvendo l’equazione:
dL(λ )
=0
dλ
n
E’ preferibile dapprima calcolare: l = ln L = ∑ ln f ( x j , λ ) e poi farne la derivata. La posizione dei
j =1
massimi di L(λ) e di ln L(λ) e’ la stessa.
Se si considera un solo parametro λ, si puo’ risolvere l’equazione:
n
dl d ln L n d
f' n
l'=
=
=∑
ln f ( x j , λ ) = ∑ = ∑ ϕ ( x j , λ )
dλ
dλ
j =1 dλ
j =1 f
j =1
Se i paramtri sono k, si dovra’ risolvere il sistema di equazioni:
dl
= 0 con i=1,2,…,k
dλi
Stima dell’errore
Se il numero delle osservabili e’ grande, L tende ad una gaussiana, almeno in prossimita’ del
massimo, e l tende ad una funzione parabolica nella regione in cui la sua derivata si annulla. La
miglior stima del parametro λ e’ il valore λ0 che rende massime sia L che l. La precisione con cui si
determina λ0 e’ determinata dalla condizione:
2
l (λ0 ± δ λ ) = lmax − 1 che e’ equivalente alla: (δ λ ) = σ 2 ( L)
2
33
−1 / 2
⎛ ∂ 2l ⎞
Infatti, nel caso in cui L e’ circa gaussiana, si ha: σ ( L) = ⎜⎜ − 2 ⎟⎟
⎝ ∂λ ⎠ λ0
Nel caso piu’ generale di piu’ parametri , i valori di essi si ottengono risolvendo il sistema:
dl
= 0 ⇒ λi
dλi
Se L e’ gaussiana:
⎞
⎛ σ λ21
⎟
⎜
2
σ
⎟
⎜
∂ 2l
λ2
H ij = −
Eij = (H −1 )ij Eij = ⎜
⎟
∂λi ∂λ j
O
⎟
⎜
2 ⎟
⎜
σ
λk ⎠
⎝
Stima di μ e media pesata
La misura di una grandezza fisica ha un comportamento assimilabile a quello di una variabile
casuale normale con madia μ. La generica misura xj abbia varianza sj2. La probabilita’ a posteriori
di ottenere un valore di x compreso tra xj e xj+dxj e’ data da:
f ( x j , μ )dx j =
1
e
2π s j
Se le misure sono n, allora:
n
L=∏
j =1
(
⎡ x j −μ
−⎢
2
⎣⎢ 2 s j
(
⎡ x j −μ
⎢
2 s 2j
−
⎢
1
e ⎣
2π s j
)2 ⎤⎥
⎦⎥
dx j
)2 ⎤⎥
⎥⎦
2
1
1 n ⎧⎪ (x j − μ ) ⎫⎪ n
l = ln L = − ∑ ⎨−
⎬ + ∑ ln
2
sj
2 j =1 ⎪⎩
2π s j
⎪⎭ j =1
Se vogliamo stimare μ, dobbiamo risolvere l’equazione:
xj
dl 1 n ( x j − μ )
1
l'=
= 2∑
= 0 ⇒ ∑ 2 − μ∑ 2 = 0
2
dμ 2 j =1 s j
sj
sj
xj
μ=
∑s
2
j
1
∑ s2
j
valore medio delle misure, ciascuna pesata sull’inverso dell’errore al quadrato
Se le sj sono tutte uguali: μ =
1
∑ xi = x
n
Errore su μ:
1
∂ 2l
= −∑ 2
2
sj
∂μ
⎛ ∂ 2l ⎞
σ μ = ⎜⎜ − 2 ⎟⎟
⎝ ∂μ ⎠
−1 / 2
=
1
1
∑s
2
j
Media pesata: esempio.
34
Supponiamo di misurare la tensione di una cella fotovoltaica.
n1 = 40 misure V1 = 1.021 V sV1 = 0.010 V
Prendiamo piu’ confidenza e impariamo a migliorare lo strumento usandolo meglio, miglioriamo la
precisione intrinseca dell’apparato (sv) di 2.5 volte:
n2 = 10 misure V2 = 1.019 V sV2 = 0.004 V
0.01
0.004
=
0
.
0016
V
σ
=
= 0.0013 V
V
1
2
40
10
Il confronto mostra che il fatto di fare piu’ misure decresce l’errore come 1 / n , ma questo non e’
cosi’ importante come migliorare decisamente la precisione dell’apparato.
Combiniamo le due serie di misure:
V
40
10
∑ σ i2 (0.01) 2 (1.021) + (0.004) 2 (1.019)
i
V =
=
= 0.39(1.021) + 0.61(1.019) = 1.0196 V
1
40
10
+
∑σ 2
(0.01) 2 (0.004) 2
i
σV =
σV =
1
1
σ V2
+
1
= 0.0010 V
1
σ V2
2
Sebbene vi siano 40 misure nella prima serie e solo 10 nella seconda, nella valutazione della media
il risultato della seconda serie pesa circa il doppio perche’ il suo errore e’ 2.5 volte minore.
Stima di σ2(noto μ )
Sia noto μ e incognita σ2 (con le sj tutte uguali).
f ( x, μ , σ ) =
1
e
2π σ
⎡ ( x − μ )2 ⎤
⎥
−⎢
⎢⎣ 2σ 2 ⎥⎦
n
( x − μ )2
⎛ 1 ⎞ − ∑ 2i σ 2
L = ∏ f ( xi , μ ,σ ) = ⎜
⎟ e
i =1
⎝ 2π σ ⎠
n
1
l = ln L = − ln(2πσ 2 ) −
( xi − μ ) 2
2 ∑
2
2σ
∂l
n 2π
1
l'=
=−
+
( xi − μ ) 2
2
2
2 2 ∑
∂σ
2 2πσ
2(σ )
2
Per determinare σ si deve porre: l’=0
n
∑ ( xi − μ ) 2 = 0 ⇒ σˆ 2 = ∑ ( xi − μ ) 2
−
+
n
2σ 2
2(σ 2 ) 2
n
Errore su σ2:
⎤
⎡
⎢
1 ⎥
⎥
σˆ 2 = ⎢−
∂ 2l ⎥
⎢
⎢ ∂ (σ 2 ) 2 ⎥ 2 2
⎦ σ =σˆ
⎣
35
( xi − μ ) 2 ⎛
n
∂ 2l
2 ⎞
⎜⎜ − 2 3 ⎟⎟
=
+∑
2 2
2 2
∂ (σ )
2(σˆ )
2
⎝ (σˆ ) ⎠
La l” va calcolata per σ 2 = σˆ 2 =
∑ (x
i
− μ )2
:
n
⎛ ∂ 2l ⎞
n
nσˆ 2 ⎛ 2 ⎞
n
⎜⎜
⎟ =
+
⎜− 6 ⎟ = − 4
2 2 ⎟
4
2 ⎝ σˆ ⎠
2σˆ
⎝ ∂ (σ ) ⎠σˆ 2 2σˆ
Quindi:
2σˆ 4
Var (σˆ ) =
n
2
⇒ σ σˆ 2 =
2 2
σˆ
n
N.B.: se non conosciamo μ e lo stimiamo con x allora σ2 e’ stimato da s 2 =
quindi σ s22 =
1
( xi − x ) 2 e
∑
n −1
2σ 4
(n − 1)
Distribuzione di Bernoulli: stima di p
Un evento a di probabilita’ incognita p si e’ presentato x volte in n prove. Qual e’ il valore piu’
probabile di p? Vogliamo fare una stime di p.
⎛n⎞
Distribuzione di Bernoulli: la probabilita’ di ottenere x successi in n prove e’ pari a ⎜⎜ ⎟⎟ p x (1 − p ) n − x
⎝ x⎠
Scegliamo una funzione di verosimiglianza:
⎛n⎞
x!
L( x, p ) = ⎜⎜ ⎟⎟ p x (1 − p ) n − x =
p x (1 − p ) n − x
n!(n − x)!
⎝ x⎠
che va intesa come una funzione della sola p (il nostro parametro).
⎛n⎞
l = ln L = x ln p + (n − x) ln(1 − p) + ln⎜⎜ ⎟⎟
⎝ x⎠
Per stimare p occorre risolvere: l’=0
dl x n − x
x − xp − np + xp
x
l'=
= 0 ⇒ x − np = 0 ⇒ p =
= −
=0⇒
dp p 1 − p
p(1 − p)
n
x
Pertanto la frequenza relativa ν = e’ la stima di massima verosimiglianza del parametro p della
n
distribuzione binomiale.
Per n → ∞ si ha: ν → p (stima consistente)
E(ν)=p (stima corretta)
Se ripetiamo la serie di n prove r volte, ottenendo r valori {x1, x2, …, xr}, allora:
r
⎛n⎞
L( xi , p) = ∏ ⎜⎜ ⎟⎟ p xi (1 − p) n − xi
i =1 ⎝ xi ⎠
r
r
r
⎛n⎞
l = ln L = ∑ xi ln p + ln(1 − p)∑ (n − xi ) + ∑ ln⎜⎜ ⎟⎟
i =1
i =1
i =1
⎝ xi ⎠
1
dl 1
= ∑ xi −
l'=
∑ (n − xi ) = 0
1− p
dp p
∑ xi = 1 xi = 1 ν = ν
p=
∑ n r∑ i
nr
r
36
(frequenza relativa media)
Distribuzione di Poisson: stima di λ
Sia λ il parametro stimatore del valore medio della distribuzione di Poisson:
λx e − λ
f ( x, λ ) =
x!
In n prove otteniamo { x1, x2, …, xn}, con σ i = ± xi e ∑ xi = N .
La funzione di verosimiglianza per il dato campione e’:
n
λ xi e − λ
L=∏
xi !
i =1
l = ln L = ∑ {xi ln λ − ln ( xi !) − λ }
dl
⎧x
⎫ 1
= ∑ ⎨ i − 1⎬ = ∑ xi − n
dλ
⎩λ ⎭ λ
La stima di verosimiglianza di λ si ottiene risolvendo: l’=0
1
n
∑ xi = x
⇒ =
⇒λ =
λ ∑ xi
n
x
x e’ uno stimatore corretto e ha varianza minima: σ x2 =
n
⎞
1
⎛ 1⎞ ⎛
⎟ = 1 =x
σ x2 = ⎜ − ⎟ = ⎜⎜ −
2 ⎟
⎝ l" ⎠ x ⎝ (∑ xi )/ λ ⎠ x nx n
x2
Quindi la stima di massima verosimiglianza del valore medio di una variabile di Poisson e’ data da:
x
λˆ = x σ λˆ =
n
x
σ λˆ
n = 1 = 1 = 1
=
ˆ
x
xn
λ
∑ xi N
l'=
In una sola prova: λˆ = xi σ λˆ = xi
σ λ2ˆ = xi
Se gli intervalli di tempo ti in cui si effettuano i conteggi xi non sono uguali:
(λti ) xi e − λti ˆ ∑ xi N σ λˆ
1
P ( xi ) =
λ=
=
=
xi !
∑ ti T λˆ N
37
Stima. Stimatori e loro proprieta’
Uno degli scopi della statistica inferenziale e’ quello di ottenere informazioni circa i parametri della
popolazione, che devono essere considerati fissi, a partire dai valori determinati in base al
campione, che sono invece variabili casuali. I parametri, infatti, quali μ e σ, sono delle costanti
numeriche, mentre i corrispondenti stimatori x e s sono variabili casuali che seguono una
distribuzione di probabilita’.
Il fine e’ quello di ottenere dai valori campionari indicazioni quanto piu’ precise possibile circa il
valore vero delle quantita’ ignote, stime quanto piu’ possibile vicine ai parametri cercati. La
metodologia adatta a raggiungere questo scopo costituisce una procedura che viene detta stima; si
parla di stima puntuale quando fornisce un singolo valore del parametro in studio, oppure di stima
per intervallo se consente di costruire un intervallo (fornisce due numeri) entro cui si puo’ supporre
che il parametro sia compreso.
La stima dei parametri di una popolazione consiste nel determinare uno stimatore, ossia una
funzione t(x1, x2, …, xN) delle N determinazioni sperimentali xi della grandezza x che costituiscono
il campione, che fornisce un valore “approssimato” del parametro. Nel caso della media, ad
∑ xi . Il valore di uno stimatore per un dato campione e’ detto
esempio, la funzione t vale: x =
N
stima.
Uno stimatore e’ una funzione di variabili casuali e, pertanto, una variabile casuale esso stesso; si
puo’ parlare di valore medio e varianza di uno stimatore riferendoci alla popolazione dei possibili
valori della stima in corrispondenza di tutti i possibili campioni.
Per derivare uno stimatore puntuale, i criteri di stima piu’ usati sono: il metodo di massima
verosimiglianza e il metodo dei minimi quadrati.
Proprieta’ degli stimatori
Ad uno stimatore si possono associare diverse caratteristiche che ne individuano la “bonta’”. Un
buon stimatore deve essere:
- consistente
- corretto
- efficiente
Indichiamo con a la quantita’ da stimare e con â lo stimatore. Ad es.: a≡μ; â= x
L’applicazione di uno stimatore â al campione di dati di N misure porta alla stima di a.
Questa potra’ variare dal valore vero, a causa di fluttuazioni statistiche del campione. Pero’ se le
misure sono indipendenti e non ci sono errori sistematici, per la legge dei grandi numeri questi
effetti diventano sempre piu’ piccoli per N → ∞. Sembra ragionevole richiedere che per un buon
stimatore la differenza fra stima e valore vero → 0 per N → ∞.
Uno stimatore e’ consistente quando converge (in probabilita’) al valore vero del parametro:
lim â = a
N →∞
P(â=a) → 1: a mano a mano che la dimensione del campione aumenta, la stima ottenuta tende al
valore vero.
Condizione sufficiente e’ che la varianza dello stimatore → 0 per N → ∞.
Esempio: la media x e’ uno stimatore consistente, infatti:
⎛ σ2 ⎞
⎛ σ2 ⎞
⎟ =1
lim P( x − μ < ε ) ≥ lim ⎜⎜1 − x ⎟⎟ = lim ⎜1 −
N →∞
N →∞
ε ⎠ N →∞⎜⎝ n ε ⎟⎠
⎝
38
(disuguaglianza di Cebycev)
La media, il valore medio di un campione, converge in probabilita’ alla media della popolazione:
P
x⎯
⎯→
μ
Per N finito non possiamo sperare che per un particolare campione di dati â abbia lo stesso valore di
a; puo’ essere piu’ grande o piu’ piccolo. Possiamo richiedere che la probabilita’ di sovrastima
bilanci quella di sottostima e in media coincida con il valore vero. Lo stimatore e’ corretto, cioe’
non distorto, senza “bias” se: E[â]=a ovvero se mediamente coincide con il valore vero di a.
Esempio: la media x e’ uno stimatore corretto, poiche’:
E (x ) = μ
(la media di tutte le medie campionarie e’ uguale a μ)
Il valore di â dipende dal campione, per cui â variera’ da campione a campione. Se la stima deve
essere una buona misura del valore vero a, la dispersione dei suoi possibili valori deve essere la piu’
piccola possibile. Uno stimatore e’ detto efficiente quando ha una piccola dispersione misurata dalla
σâ2 (piccola varianza).
Se â1 e â2 sono ambedue stimatori non distanti di a, ma vale σ12< σ22, e’ da considerarsi preferibile
â1 che viene definito piu’ efficiente o piu’ preciso.
Esempio:
E[ x ] = μ σ x =
σx
;
m=mediana E[m] = μ
N
σ m2 > σ x2 ⇒ il valore medio e’ piu’ efficiente di m
Approfondimento
E’ possibile dimostrare che per ogni stimatore â di a esiste un limite inferiore della varianza dello
stimatore σâ2 e quindi un limite superiore per la sua efficienza (teorema di Cramer-Rao). Per uno
stimatore corretto non distorto:
1
σ a2ˆ ≥
= k (a)
⎡⎛ ∂ ln L ⎞ 2 ⎤
E ⎢⎜
⎟ ⎥
⎢⎣⎝ ∂a ⎠ ⎥⎦
dove L e’ la funzione di verosimiglianza:
L( x1 , x2 ,..., xn ) = P ( x1 , a ) P ( x2 , a )...P ( xn , a ) = ∏ P ( xi , a )
Il teorema puo’ essere anche riscritto come:
σ a2ˆ ≥ −
1
⎡⎛ ∂ 2 ln L ⎞⎤
⎟
E ⎢⎜⎜
2 ⎟⎥
⎣⎝ ∂a ⎠⎦
Nota su: σ x2 ,σ x2 , s x2 , s x2
Supponiamo che siano ottenute da un campione di n {x1} normali.
s
1
sx =
sx = x
( xi − x ) 2
∑
n −1
n
σx
σs
sx
1
σs ≈
≈
≈
s
2(n − 1)
2(n − 1)
2(n − 1)
39
Si voglia misurare σ. A livello di progetto si voglia valutare quante misure occorrono per ottenere
una data precisione di σ.
Se si vuole raggiungere un errore di circa il 10%;
se prevediamo n=50 misure di xi:
σs
1
=
= 10%
s
2(50 − 1)
se σ=6 e’ una ragionevole assunzione:
6
≈ 0.6
σs ≈
2(50 − 1)
sx
A livello di analisi, se non conosciamo σ ma vogliamo stimarla: σ s x ≈
2(n − 1)
s x = 6 n = 50 σ s x = 0.6 s x = 6.0 ± 0.6
Vi e’ differenza tra un errore ottenuto dal campione in questo modo e una conoscenza a priori di σx
(s → ∞ per n → ∞).
Vi e’ differenza tra i due risultati:
σ
0.2
= 0.1
1) μ = 10.0 ± 0.1 dove σ x = 0.2 e’ noto, n=4 misure, x = 10.0 e σ x = x =
2
n
2) μ = 10.0 ± 0.1 dove σ x non e’ noto e viene stimato sui 4 valori {xi}:
s
1
0.2
s x2 =
( xi − x ) 2 = 0.2
sx = x =
= 0.1 x = 10.0
∑
2
n −1
n
Tale differenza e’ importante per piccoli n (piccoli campioni):
x−μ
x = x ± s x richiede l’uso di Student t =
sx
Per grandi campioni (n grande) la stima di σ migliora e la differenza e’ meno importante:
x−μ
x = x ± σ x richiede z =
σx
40










