CORSO DI LAUREA IN MATEMATICA - a.a. 2009

 1 CORSO DI LAUREA IN MATEMATICA - a.a. 2009-2010
Compito di FISICA 1 - 20-7-2010
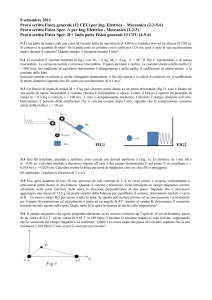
Una sferetta rigida e omogenea(S) e un anello rigido e omogeneo(A) di spessore trascurabile,
di massa mA = 2Kg e mS = 2mA e con lo stesso raggio r = 2cm, partono insieme da fermi
dalla sommitá di un piano inclinato (θ = 30o ) lungo L = 3m. La prima metá del pano inclinato
é perfettamente liscia, mentre la seconda ha un coefficiente di attrito µ = 0.05
1) Chi arriva prima a metá del piano inclinato e in quanto tempo?
2) Chi arriva prima in fondo al piano inclinato e in quanto tempo?
3) Determinare tutti i parametri cinematici e l’energia cinetica di A ed S quando arrivano
in fondo al piano inclinato.
4) Confrontare i risultati ottenuti per A ed S nelle domande 1,2,3 e commentare/spiegare
le uguaglianze e le differenze.
5) Rispondere alle domande 2 e 3 se µ = 0.4
Osservazioni e suggerimenti:
Si spieghino e si giustifichino le formule che vengono utilizzate.
Si indichi con chiarezza il sistema di riferimento utilizzato
Nei limiti del possibile si usino i simboli proposti nel testo.
Si cerchi di fare tutti i calcoli con i simboli e si sostituiscano i numeri solo per calcolare
il risultato finale.
• Si usi g = 9.81m/s2 e si diano i risultati numerici con la precisione corrispondente.
• Si tenga conto delle unitá di misura nei passaggi con i valori numerici.
•
•
•
•
Risultati Numerici:
1: ts = ta = 0.782s
2: ts = ta = 1.110s
3: vscm = vacm = 5.31m/s, ωs = 17.42s−1 , ωa = 6.97s−1 , Ks = 56.4J, Ka = 28.17J
5: ts = ta = 1.147s,
. vscm = vacm = 4.39m/s, ωs = 155.0s−1 , ωa = 62.0s−1 , Ks = 46.16J, Ka = 20.77J
2 CORSO DI LAUREA IN MATEMATICA - a.a. 2009-2010
Compito di FISICA 1 - 7-9-2010
Un’asta rigida, omogenea, sottile AB di lunghezza L = 1.50m e massa m = 4.50Kg è
vincolata a ruotare in un piano verticale intorno ad un suo estremo A senza attrito. Al suo
altro estremo B é attaccato un filo ideale che passa intorno ad una carrucola C di massa e
dimensioni trascurabili con la distanza AC = AB. Al filo é attaccato un corpo di massa m1 (v.
figura).
1) Determinare il valore di m1 perché il sistema sia in equilibrio nella posizione ϕ0 = π/6.
2) Verificare che l’equilibrio in ϕ0 = π/6 é instabile.
3) Se si sposta l’asta di un piccolo angolo verso l’alto, determinare l’equazione di moto del
sistema e in particolare determinare con quale velocitá l’asta passa dalla posizione verticale.
4) Determinare la tensione del filo quando l’asta passa dalla posizione verticale.
B
C
A
2ϕ
m1
Osservazioni e suggerimenti:
• La domanda 1) puó essere risolta in due modi diversi (ugualmente semplici): uno dei due
modi serve anche per rispondere alle domande 2) e 3); l’altro alla domanda 4).
• Si spieghino e si giustifichino le formule che vengono utilizzate.
• Si indichi con chiarezza il sistema di riferimento utilizzato
• Nei limiti del possibile si usino i simboli proposti nel testo.
• Si facciano tutti i calcoli con i simboli e si sostituiscano i numeri solo per ottenere il
risultato finale.
• Si usi g = 9.81m/s2 e si diano i risultati numerici con la precisione corrispondente.
• Si tenga conto delle unitá di misura nei passaggi con i valori numerici.
Risultati Numerici:
1: m1 = 2.25Kg
3: ω = 0.723s−1
4: T = 16.2N
3 CORSO DI LAUREA IN MATEMATICA - a.a. 2009-2010
Compito di FISICA 1 - 23-9-2010
Un pendolo semplice di lunghezza L = 1.30m e massa ma = 3.50Kg parte da fermo con un
angolo θ0 = 30o rispetto all’orizzontale.
1) Determinare la velocitá v1 , l’energia cinetica K1 e la tensione del filo di sospensione
quando arriva nella posizione verticale.
2) Nella posizione verticale urta in modo completamente elastico un secondo pendolo semplice, sospeso nello stesso punto, della stessa lunghezza e di massa mb . Descrivere il moto
dopo l’urto e in particolare determinare la massima altezza raggiunta da ma e mb nei due casi:
mb = ma ed mb = ma /3.
3) Rispondere alla domanda 2 nel caso che l’urto sia completamente anelastico.
4) Fare il bilancio energetico complessivo di ma ed mb per tutti i casi delle domande 2 e 3,
quando mb raggiunge la massima altezza.
Osservazioni e suggerimenti:
Si spieghino e si giustifichino le formule che vengono utilizzate.
Si indichi con chiarezza il sistema di riferimento utilizzato
Nei limiti del possibile si usino i simboli proposti nel testo.
Si cerchi di fare tutti i calcoli con i simboli e si sostituiscano i numeri solo per calcolare
il risultato finale.
• Si usi g = 9.81m/s2 e si diano i risultati numerici con la precisione corrispondente.
• Si tenga conto delle unitá di misura nei passaggi con i valori numerici.
•
•
•
•
1:
2:
3:
4:
Risultati Numerici:(origine e riferim. energia potenziale nel punto piú basso)
v1 = 1.849m/s; K1 = 5.98j; T = 43.53N
mb = ma : ha = 0m, hb = 0.174m; mb = ma /3 : ha = 0.0435m, hb = 0.392m
mb = ma : h = 0.0435m; mb = ma /3 : h = 0.0980m
urto anelastico: mb = ma : E = 2.99J; mb = ma /3 : E = 4.49J
4 CORSO DI LAUREA IN MATEMATICA - a.a. 2009-2010
Compito di FISICA 1 - 2-2-2011
Una palla di biliardo, assimilabile ad una sfera omogenea di raggio R e massa M , inizialmente
ferma su un piano orizzontale, é colpita da una stecca che imprime un impulso J ad una altezza
h rispetto al piano. J é orizzontale e giace nel piano verticale che contiene il punto di appoggio
tra sfera e piano (v.figura). Sia v la velocitá del CM e ω la velocitá angolare della sfera, e si
indichi con tf l’istante, se esiste, in cui vf e ωf divengono costanti. Si determini, per ognuno
dei casi sottoindicati, v0 e ω0 immediatamente dopo l’urto e il valore di tf , vf e ωf , quando é
presente un attrito µ = 0.08 tra sfera e piano di appoggio.
1) h1 = R
2) h2 = 4R/3
3) h3 = 7R/5
4) h4 = R/2
5) Si confronti l’energia cinetica K0 immediatamente dopo l’urto con l’energia cinetica finale
Kf nel caso 4) e, possibilmente, si giustifichi la differenza.
Valori numerici J = 1.50N s, R = 6.15cm, M = 220g
h
R
Osservazioni e suggerimenti:
- L’esercizio richiede di studiare il moto in presenza di attrito. Tuttavia, se si incontrano
problemi, puó essere opportuno almeno risolvere i casi 1 e 3 in assenza di attrito (cioé con
µ = 0)
- Si noti che i 4 casi prospettati differiscono solo per le condizioni iniziali e che possono essere
risolti scrivendo una sola volta le equazioni in forma generale (e corretta).
Si spieghino e si giustifichino le formule che vengono utilizzate.
Si indichi con chiarezza il sistema di riferimento utilizzato
Nei limiti del possibile si usino i simboli proposti nel testo.
Si cerchi di fare tutti i calcoli con i simboli e si sostituiscano i numeri solo per calcolare
il risultato finale.
• Si usi g = 9.81m/s2 e si diano i risultati numerici con la precisione corrispondente.
• Si tenga conto delle unitá di misura nei passaggi con i valori numerici.
•
•
•
•
1:
2:
3:
4:
Risultati Numerici(verso positivo dele rotazioni entrante, A punto di contatto):v0 = 6.82m/s
ω0 = 0s−1 ,
(vA0 = 6.82m/s), tf = 2.48s, vf = 4.87m/s, ωf = 79.2s−1
ω0 = 92.4s−1 , (vA0 = 1.13m/s), tf = 0.414s, vf = 6.49m/s, ωf = 105.6s−1
ω0 = 110.9s−1 , (vA0 = 0m/s), tf = 0s
ω0 = −138.6s−1 , (vA0 = 15.34m/s), tf = 5.58s, vf = 2.43m/s, ωf = 39.6s−1
5 CORSO DI LAUREA IN MATEMATICA - a.a. 2009-2010
Compito di FISICA 1 - 15-2-2011
Una blocchetto di dimensioni trascurabili e di massa m, parte da fermo dalla sommitá di un
piano inclinato (altezza h e lunghezza L). Il blocchetto scivola lungo il piano inclinato fino a
raggiungere l’estremo di una molla (costante k, lunghezza di riposo d) solidalmente connessa alla
fine del piano inclinato (v. figura, non in scala). Si chiede di calcolare la massima compressione
della molla, l’altezza a cui eventualmente risale il blocchetto (che NON rimane attaccato alla
molla) e il lavoro totale fatto dalla forza di attrito -quando presente- nei seguenti casi:
1) µs = µd = 0
2) µs = µd = 0.1
3) µs = µd = 0.55
Valori numerici m = 150g, L = 5, 00m, h = 2, 50m, k = 5, 00N/m, d = 125cm
m
h
L
k,d
Osservazioni e suggerimenti:
-se si trova difficoltá a scrivere le equazioni in generale, si inizi con il calcolare la velocitá di m
quando arriva, dall’alto, in contatto con la molla e quando abbandona la molla risalendo verso
l’alto
Si spieghino e si giustifichino le formule che vengono utilizzate.
Si indichi con chiarezza il sistema di riferimento utilizzato
Nei limiti del possibile si usino i simboli proposti nel testo.
Si cerchi di fare tutti i calcoli con i simboli e si sostituiscano i numeri solo per calcolare
il risultato finale.
• Si usi g = 9.81m/s2 e si diano i risultati numerici con la precisione corrispondente.
• Si tenga conto delle unitá di misura nei passaggi con i valori numerici.
•
•
•
•
Risultati Numerici:
1: ∆x = 1.208m, hf = h
2: ∆x = 1.085m, hf = 1.786m, Lattr = −1.050J
3: ∆x = 0.236m, hf :non risale, Lattr = −2.79J
6 Fac. SMFN - CdL triennale in Matematica - a.a. 2006/2007
Prova scritta di Elementi di Fisica I - 04 Settembre 2007
Un disco omogeneo (M = 8.00 Kg, R = 40.0 cm) può ruotare, senza attrito, attorno ad un
asse verticale (posto nel suo centro) in un piano orizzontale. Ad una distanza d = 0.95 R dal suo
centro un cubetto di massa m1 = 400g (assimilabile ad un punto materiale) è appoggiato sul disco
ed il coefficiente di attrito statico fra cubetto e disco è µs = 0.600. Attorno al bordo del disco è
fissata ed avvolta una funicella ideale che, tramite un’opportuna puleggia (priva di attrito e di massa
trascurabile) è agganciata ad un corpo di massa m = 0.400 Kg, che può muoversi lungo la verticale
sotto l’effetto della propria forza peso. Il sistema è inizialmente fermo ed è poi lasciato libero di
muoversi sotto l’azione delle forze applicate.
Si chiede di determinare:
1. l’accelerazione con cui cade m;
2. la tensione a cui è sottoposta la funicella da parte di m durante la caduta;
3. l’energia cinetica ed il momento angolare di tutto il sistema dopo 1 s di moto;
4. il tempo τ nel quale il cubetto m1 comincia a muoversi rispetto al disco ed il moto successivo
di m1 nell’ipotesi che abbandoni subito il disco dopo il distacco;
5. l’energia cinetica di tutto il sistema al tempo τ (cioè quando m1 è ancora appoggiato sul disco)
e al tempo 2τ e commentare i risultati trovati.
Osservazioni e suggerimenti:
• Si spieghino e si giustifichino le formule utilizzate.
• Si indichi con chiarezza il sistema di riferimento utilizzato.
• Usare possibilmente i simboli proposti nel testo.
• Utilizzare i simboli in tutti i passaggi e SOLO alla fine sostituire i valori numerici.
• Si usi il valore g = 9.81m/s2 e si diano i risultati con la precisione corrispondente.
• Inserire sempre le unitá di misura quando si considerano i valori numerici.
7 Fac. SMFN - CdL triennale in Matematica - a.a. 2010/2011
Prova scritta di FISICA I ed Elementi di Fisica I - 06 Settembre 2011
Un ingranaggio può essere schematizzato come due cilindri rigidi, omogenei, posti in un piano
orizzontale, di massa e raggio rispettivamente (m,r) e (M,R), ruotanti rispetto a due assi verticali
fissi, di tracce O’ e O (v. Fig.), e posti a contatto lungo una comune generatrice di traccia P
(v. Fig.). L’ingranamento è tale che i due cilindri non possono scivolare l’uno rispetto all’altro
(cioè i punti di contatto in P dei due cilindri hanno la stessa velocità lineare). L’asse O’ del
cilindro minore è costituito da un filo elastico di costante elastica di torsione k, mentre l’asse
O del cilindro maggiore è inizialmente privo di attrito; in modo quasi statico si provoca una
rotazione di un angolo α◦ del cilindro minore in direzione oraria e al tempo t = 0 si abbandona
il sistema all’effetto delle forze e dei momenti meccanici applicati. Si chiede di determinare:
y
1. l’ampiezza e la direzione dell’angolo di rotazione
del cilindro maggiore corrispondente alla rotazione iniziale α◦ del cilindro minore;
R
2. l’equazione di moto del cilindro minore ed in
particolare il valore massimo del modulo della
sua accelerazione angolare;
O
P
r
O’
x
3. il periodo di oscillazione del sistema;
4. il bilancio energetico dei due cilindri costituenti il sistema durante il moto;
5. l’espressione della forza tangenziale che si esercita in P sul cilindro minore ed il suo valore
quando l’angolo di rotazione del cilindro è nullo;
6. se, invece, l’asse del cilindro maggiore O presentasse attrito di rotazione, di modulo µ, cosa
cambierebbe nelle risposte alle domande precedenti. In particolare dopo quanto tempo il
cilindro minore dimezzerebbe il valore della sua massima velocità angolare.
Valori numerici: |α◦ | = 10.0◦ ; R = 1.5 · r = 30.0 cm; m = M/2 = 4.00 Kg; k = 4.50 J/rad; µ =
0.250 N · m.
• Si spieghino e si giustifichino le formule utilizzate.
• Si indichi con chiarezza il sistema di riferimento utilizzato.
• Usare possibilmente i simboli proposti nel testo.
• Utilizzare i simboli in tutti i passaggi e SOLO alla fine sostituire i valori numerici.
• Si usi il valore g = 9.81m/s2 e si diano i risultati con la precisione corrispondente.
• Inserire sempre le unitá di misura quando si considerano i valori numerici.
8 Fac. SMFN - CdL triennale in Matematica - a.a. 2008/2009
Prova scritta di FISICA I ed Elementi di Fisica I - 08 Febbraio 2010
Su un piano orizzontale, liscio, si muovono, sulla stessa retta, due corpi (assimilabili a punti
materiali) di massa e velocità rispettivamente m1 = 5.00 Kg e v1 = 12.0 Km/h, e m2 = 2.00Kg e
v2 = 40.0 Km/h; i vettori v1 e v2 sono concordi ed hanno la stessa direzione. Al tempo t = 0 il corpo
m1 precede m2 di un tratto d = 10.0 m e porta attaccata sul retro (cioè dalla parte di m2 , che segue)
una molla di costante elastica k = 105 N/m; la molla ha massa trascurabile (rispetto a m1 e m2 ), è
molto compatta, ha l’estremo verso m2 libero ed è in condizioni di riposo. Si chiede di determinare:
1. il tempo nel quale i due corpi si urteranno, cioè quando verranno a contatto tramite l’inizio
della compressione della molla.
Supponendo che l’intervallo di tempo in cui la molla resta compressa sia brevissimo, cioè trascurabile
rispetto ai tempi caratteristici del moto dei due corpi, in altre parole, in modo da poter considerare
tutto l’atto di compressione e successiva dilatazione della molla come un urto, si determini anche:
2. l’energia cinetica totale del sistema dei due corpi prima dell’urto;
3. la verifica del teorema di Koenig per l’energia cinetica del sistema m1 + m2 ;
4. la compressione massima della molla durante l’urto;
5. il moto di m1 e m2 dopo l’urto.
Si chiede infine di ripetere tutte la valutazioni di cui sopra nel caso in cui il piano orizzontale sia
scabro e presenti coefficienti di attrito dinamico rispettivamente µ1 = 0.3 e µ2 = 0.1.
• Si spieghino e si giustifichino le formule utilizzate.
• Si indichi con chiarezza il sistema di riferimento utilizzato.
• Usare possibilmente i simboli proposti nel testo.
• Utilizzare i simboli in tutti i passaggi e SOLO alla fine sostituire i valori numerici.
• Si usi il valore g = 9.81m/s2 e si diano i risultati con la precisione corrispondente.
• Inserire sempre le unitá di misura quando si considerano i valori numerici.
9 Fac. SMFN - CdL triennale in Matematica - a.a. 2008/2009
Prova scritta di Elementi di Fisica I - 08 Settembre 2009
Una sbarra lineare, rigida, omogenea, di massa M = 3.00 Kg e lunghezza L = 1.50 m, è vincolata
a scorrere, senza attrito, con un suo estremo ad una parete verticale (rimanendo sempre agganciata
a questa parete) e con l’altro estremo appoggiato sul pavimento orizzontale, pure liscio. È trattenuta
(nell’estremo appoggiato al pavimento) da una molla (di massa trascurabile) di costante elastica k =
1.00 · 102 N/m e la sbarra è in equilibrio quando forma un angolo di 70◦ col pavimento. Determinare,
in queste condizioni:
1. la lunghezza a riposo l◦ e l’allungamento ∆l della molla affinchè siano garantite le condizioni
di equilibrio suddette;
2. le reazioni vincolari nei due estremi della sbarra nelle condizioni sopra dette.
Viene sganciata la molla dall’estremo della sbarra, che, conseguentemente, viene abbandonata all’effetto delle rimanenti forze applicate. Determinare, durante il moto di caduta della sbarra:
3. l’accelerazione angolare e la velocità angolare della sbarra;
4. l’energia cinetica totale posseduta dalla sbarra;
5. le reazioni vincolari nei due estremi della sbarra, e commentare se il segno di queste reazioni
vincolari si mantenga costante durante il moto ;
6. la traiettoria che percorre il centro di massa della sbarra.
Per i punti 3., 4. e 5. determinare i valori numerici delle grandezze fisiche indicate
per θ = 0.◦ .
Osservazioni e suggerimenti:
• Si spieghino e si giustifichino le formule utilizzate.
• Si indichi con chiarezza il sistema di riferimento utilizzato.
• Usare possibilmente i simboli proposti nel testo.
• Utilizzare i simboli in tutti i passaggi e SOLO alla fine sostituire i valori numerici.
• Si usi il valore g = 9.81m/s2 e si diano i risultati con la precisione corrispondente.
• Inserire sempre le unitá di misura quando si considerano i valori numerici.
• Si consiglia di utilizzare come parametro indipendente per descrivere il moto della
sbarra l’angolo formato dalla sbarra col pavimento
10 Fac. SMFN - CdL triennale in Matematica - a.a. 2010/2011
Prova scritta di FISICA I ed Elementi di Fisica I - 09 Giugno 2011
Un’asta rigida AB, di lunghezza 1.80 m e di densità lineare µ = 20.0 g/cm, è posta in un piano verticale ed il suo estremo A è vincolato, senza attrito, ad una parete verticale; in C (tale che CB = 30.0
cm) è agganciata ad una molla (di costante elastica k e lunghezza a riposo l◦ ), che è fissata al pavimento orizzontale in D. La distanza di A dal pavimento è h = 1.00 m (v. Fig. non in scala). Si chiede di
determinare:
1. il valore di k in modo che l’asta sia in equilibrio in posizione orizzontale quando la molla risulti compressa del A
3% rispetto al suo valore a riposo.
C
B
h
Abbassata successivamente, in modo quasi statico, la quota
di C di 2.00 cm, si determini inoltre:
D
2. l’accelerazione angolare dell’asta quando viene abbandonata all’effetto della forza peso, della
forza elastica della molla e della reazione vincolare in A;
3. il periodo delle piccole oscillazioni dell’asta;
4. la velocità del centro di massa dell’asta quando passa dalla posizione orizzontale;
5. l’espressione della reazione vincolare in A durante il moto dell’asta;
6. (facoltativa) cosa cambierebbe, nelle domande precedenti, se l’asta fosse solo appoggiata alla
molla in C (e non agganciata).
• Studiare il regine delle piccole oscillazioni permette di considerare la molla praticamente sempre
verticale; in queste approssimazioni si suggerisce di utilizzare l’angolo formato dall’asta con
l’orizzontale per A, θ, per individuare la posizione dell’asta.
• Si spieghino e si giustifichino le formule utilizzate.
• Si indichi con chiarezza il sistema di riferimento utilizzato.
• Usare possibilmente i simboli proposti nel testo.
• Utilizzare i simboli in tutti i passaggi e SOLO alla fine sostituire i valori numerici.
• Si usi il valore g = 9.81m/s2 e si diano i risultati con la precisione corrispondente.
• Inserire sempre le unitá di misura quando si considerano i valori numerici.
11 Fac. SMFN - CdL triennale in Matematica - a.a. 2006/2007
Prova scritta di Elementi di Fisica I - 12 Febbraio 2008
Su un piano orizzontale, perfettamente liscio, si trova in quiete una massa m = 500 g, rappresentabile come un punto materiale. Un’asta omogenea, rigida, di sezione trascurabile, lunghezza L =
0.750 m e densità lineare λ = 20.0 g/cm trasla sul piano con velocità costante (ed uniforme per tutti
i punti dell’asta) di modulo v◦ = 9.00 Km/h e direzione ortogonale all’asta. Ad un certo istante
l’asta urta la massa m con un suo estremo. Si determini:
1. nel caso in cui l’urto sia perfettamente anelastico (cioè che m resti attaccato all’estremo dell’asta
dopo l’urto), il moto del sistema dopo l’urto, la velocità del centro di massa dell’asta e di m
dopo 1.5 s dall’urto e l’energia cinetica totale del sistema asta+m;
2. idem come al punto 1) nel caso di urto perfettamente elastico;
3. commentare il bilancio energetico (prima e dopo l’urto) nei casi 1) e 2);
4. se possa esistere (ed eventualmente quale in caso di risposta positiva) un punto dell’asta che
resti fermo dopo l’urto nei casi 1) e 2).
Osservazioni e suggerimenti:
• Si spieghino e si giustifichino le formule utilizzate.
• Si indichi con chiarezza il sistema di riferimento utilizzato.
• Usare possibilmente i simboli proposti nel testo.
• Utilizzare i simboli in tutti i passaggi e SOLO alla fine sostituire i valori numerici.
• Si usi il valore g = 9.81m/s2 e si diano i risultati con la precisione corrispondente.
• Inserire sempre le unitá di misura quando si considerano i valori numerici.
12 Fac. SMFN - CdL triennale in Matematica - a.a. 2006/2007
Prova scritta di Elementi di Fisica I - 12 Febbraio 2008
Su un piano orizzontale, perfettamente liscio, si trova in quiete una massa m = 500 g, rappresentabile come un punto materiale. Un’asta omogenea, rigida, di sezione trascurabile, lunghezza L =
0.750 m e densità lineare λ = 20.0 g/cm trasla sul piano con velocità costante (ed uniforme per tutti
i punti dell’asta) di modulo v◦ = 9.00 Km/h e direzione ortogonale all’asta. Ad un certo istante
l’asta urta la massa m con un suo estremo. Si determini:
1. nel caso in cui l’urto sia perfettamente anelastico (cioè che m resti attaccato all’estremo dell’asta
dopo l’urto), il moto del sistema dopo l’urto, la velocità del centro di massa dell’asta e di m
dopo 1.5 s dall’urto e l’energia cinetica totale del sistema asta+m;
2. idem come al punto 1) nel caso di urto perfettamente elastico;
3. commentare il bilancio energetico (prima e dopo l’urto) nei casi 1) e 2);
4. se possa esistere (ed eventualmente quale in caso di risposta positiva) un punto dell’asta che
resti fermo dopo l’urto nei casi 1) e 2).
Osservazioni e suggerimenti:
• Si spieghino e si giustifichino le formule utilizzate.
• Si indichi con chiarezza il sistema di riferimento utilizzato.
• Usare possibilmente i simboli proposti nel testo.
• Utilizzare i simboli in tutti i passaggi e SOLO alla fine sostituire i valori numerici.
• Si usi il valore g = 9.81m/s2 e si diano i risultati con la precisione corrispondente.
• Inserire sempre le unitá di misura quando si considerano i valori numerici.
13 Fac. SMFN - CdL triennale in Matematica - a.a. 2006/2007
Prova scritta di Elementi di Fisica I - 12 Febbraio 2008
Su un piano orizzontale, perfettamente liscio, si trova in quiete una massa m = 500 g, rappresentabile come un punto materiale. Un’asta omogenea, rigida, di sezione trascurabile, lunghezza L =
0.750 m e densità lineare λ = 20.0 g/cm trasla sul piano con velocità costante (ed uniforme per tutti
i punti dell’asta) di modulo v◦ = 9.00 Km/h e direzione ortogonale all’asta. Ad un certo istante
l’asta urta la massa m con un suo estremo. Si determini:
1. nel caso in cui l’urto sia perfettamente anelastico (cioè che m resti attaccato all’estremo dell’asta
dopo l’urto), il moto del sistema dopo l’urto, la velocità del centro di massa dell’asta e di m
dopo 1.5 s dall’urto e l’energia cinetica totale del sistema asta+m;
2. idem come al punto 1) nel caso di urto perfettamente elastico;
3. commentare il bilancio energetico (prima e dopo l’urto) nei casi 1) e 2);
4. se possa esistere (ed eventualmente quale in caso di risposta positiva) un punto dell’asta che
resti fermo dopo l’urto nei casi 1) e 2).
Osservazioni e suggerimenti:
• Si spieghino e si giustifichino le formule utilizzate.
• Si indichi con chiarezza il sistema di riferimento utilizzato.
• Usare possibilmente i simboli proposti nel testo.
• Utilizzare i simboli in tutti i passaggi e SOLO alla fine sostituire i valori numerici.
• Si usi il valore g = 9.81m/s2 e si diano i risultati con la precisione corrispondente.
• Inserire sempre le unitá di misura quando si considerano i valori numerici.
14 Fac. SMFN - CdL triennale in Matematica - a.a. 2006/2007
Prova scritta di Elementi di Fisica I - 12 Giugno 2007
Su un piano orizzontale scabro (µd = 0.200) é fissato l’estremo di una molla ideale (k = 103 N/m),
attaccato ad un fermo fissato sul piano. La molla è compressa di un tratto ∆l = 20.0cm; l’altro
estremo della molla é appoggiato ad un corpo di massa M = 3.00Kg, che puo’ traslare sul piano
scabro. Ad una distanza di 1.00 m da M é posta un’asta rigida, uniforme, sottile, di lunghezza
l = 1.50m e densitá lineare 20.0 gr/cm, incernierata senza attrito attorno ad un punto fisso O che si
trova ad l/10 da un estremo A dell’asta. L’asta é in quiete in posizione verticale e sfiora, con l’altro
suo estremo B, il piano orizzontale scabro; la direzione di spostamento della molla giace nel piano
verticale passante per l’asta (ferma). Si chiede di determinare:
1. liberata la molla, la velocitá di partenza di M quando si stacca dalla molla;
2. la velocitá di M immediatamente prima di urtare l’asta;
3. la velocitá di M, (in valore e segno), subito dopo l’urto ( considerato perfettamente elastico) e
dove si fermerá M;
4. l’angolo massimo che formerá l’asta, rispetto alla verticale, nel suo moto dopo l’urto;
5. la reazione vincolare (in modulo, direzione, verso) agente in O sull’asta immediatamente dopo
l’urto.
Osservazioni e suggerimenti:
• Si spieghino e si giustifichino le formule utilizzate.
• Si indichi con chiarezza il sistema di riferimento utilizzato.
• Usare possibilmente i simboli proposti nel testo.
• Utilizzare i simboli in tutti i passaggi e SOLO alla fine sostituire i valori numerici.
• Si usi il valore g = 9.81m/s2 e si diano i risultati con la precisione corrispondente.
• Inserire sempre le unitá di misura quando si considerano i valori numerici.
15 Fac. SMFN - CdL triennale in Matematica - a.a. 2010/2011
Prova scritta di FISICA I ed Elementi di Fisica I - 13 Febbraio 2012
Con riferimento alla figura, una molla ideale, di costante elastica k = 0.900·102N/m, è posta in un
piano verticale, con un estremo fissato e l’altro estremo A agganciato ad una fune ideale che, passando
nella gola di una carrucola (raggio r = 15.0 cm e massa m), vincolata a ruotare senza attrito attorno
ad un asse orizzontale di traccia O), è agganciata a due corpi M1 e M2 (M1 = 2·M2 = 2·m = 3.00 Kg,
assimilabili a punti materiali). La fune non slitta nella gola della carrucola. Il sistema è inizialmente
in quiete sotto l’azione della gravità e delle varie reazioni vincolari; si determini:
1. l’allungamento della molla in questa fase iniziale.
Al tempo t = 0 viene tagliato il filo che trattiene il corpo
M2 ; si chiede di determinare:
O
m
2. l’equazione di moto della massa M1 ;
r
3. il periodo e l’ampiezza dell’oscillazione di M1 ;
4. il massimo valore raggiunto dall’energia cinetica del corpo
M1 e dall’energia elastica della molla durante il moto del
sistema, commentando criticamente i risultati ottenuti;
A
M1
5. la reazione vincolare in O durante l’oscillazione del sistema;
6. la tensione applicata dalla fune all’estremo A della molla
durante il moto del sistema;
k
M2
7. cosa cambierebbe, nelle risposte alle domande precedenti,
se sull’asse di rotazione O della carrucola fosse presente un attrito di rotazione di modulo
τ = 0.850 · 10−1 N m.
• Si spieghino e si giustifichino le formule utilizzate.
• Si indichi con chiarezza il sistema di riferimento utilizzato.
• Usare possibilmente i simboli proposti nel testo.
• Utilizzare i simboli in tutti i passaggi e SOLO alla fine sostituire i valori numerici.
• Si usi il valore g = 9.81m/s2 e si diano i risultati con la precisione corrispondente.
• Inserire sempre le unitá di misura quando si considerano i valori numerici.
16 Fac. SMFN - CdL triennale in Matematica - a.a. 2008/2009
Prova scritta di Elementi di Fisica I - 14 Luglio 2009
In figura è schematizzato un paranco: una fune ideale, fissata in A (soffitto), passa per la gola
di una carrucola di centro O, massa m e raggio r, senza potervi strisciare, e, tramite una rotella R
(di massa e raggio trascurabili rispetto ai valori della carrucola), termina con l’altro estremo in un
punto dove può essere applicata una forza F (verticale). Sia la carrucola che la rotella non presentano
attrito rispetto al rispettivo asse di rotazione orizzontale. In O è agganciato un corpo di massa M.
Tutto il sistema si trova in un piano verticale. Determinare:
1. il valore di Feq che mantiene il sistema in equilibrio;
Se al tempo t = 0 si applica una forza costante F = 1.25 · Feq , si determini:
2. l’accelerazione con cui si muove il corpo M;
3. le tensioni della fune nei punti E, C e B;
4. il lavoro fatto dalla forza F in 1.5 s di moto del sistema;
5. l’energia cinetica acquistata dalla carrucola e dalla massa M dopo 1.5 s di moto del sistema;
6. le reazioni vincolari in A e in G durante il moto.
[Valori numerici: M = 75.0 Kg; m = 2.50 Kg; r = 15.0 cm]
A
G
E
D
R
m ,r
C
O
B
F
M
• Utilizzare i simboli in tutti i passaggi e SOLO alla fine sostituire i valori numerici.
• Si usi il valore g = 9.81m/s2 e si diano i risultati con la precisione corrispondente.
• Inserire sempre le unitá di misura quando si considerano i valori numerici.
17 Fac. SMFN - CdL triennale in Matematica - a.a. 2006/2007
Prova scritta di Elementi di Fisica I - 17 Luglio 2007
Una sfera rigida, omogenea, di massa M = 5.00 Kg e raggio R = 35.0 cm, è appoggiata su un piano
orizzontale e allo spigolo di uno scalino verticale, di altezza h= 10.0 cm rispetto al piano orizzontale,
ed è soggetta alla gravità.
Si chiede di:
1. determinare il valore di una forza orizzontale, Fm , applicata nel centro della sfera, che renda
nulla la reazione vincolare verticale del piano orizzontale su cui la sfera è appoggiata (supporre
che la reazione vincolare nello spigolo dello scalino sia sempre diretta verso il centro della sfera);
2. applicando una F > Fm in modo quasi-statico, si riesce a far salire la sfera sopra lo scalino;
determinare il lavoro che dovrà fare la forza F , nell’ipotesi che la sfera si trovi, alla fine,
praticamente ferma sopra lo scalino;
3. il piano orizzontale, sopra lo scalino, è scabro; determinare il minimo valore per il coefficiente di
attrito statico, µs , fra sfera e piano scabro, che assicura il rotolamento puro della sfera quando
la F applicata nel suo centro (sempre orizzontale) è superiore del 10% a Fm ;
4. determinare l’accelerazione del centro di massa della sfera, l’energia cinetica totale ed il momento angolare totale della sfera (nel caso di cui al punto 3) dopo 2 s di moto.
R
F
N
h
Osservazioni e suggerimenti:
• Si spieghino e si giustifichino le formule utilizzate.
• Si indichi con chiarezza il sistema di riferimento utilizzato.
• Usare possibilmente i simboli proposti nel testo.
• Utilizzare i simboli in tutti i passaggi e SOLO alla fine sostituire i valori numerici.
• Si usi il valore g = 9.81m/s2 e si diano i risultati con la precisione corrispondente.
• Inserire sempre le unitá di misura quando si considerano i valori numerici.
18 Fac. SMFN - CdL triennale in Matematica - a.a. 2008/2009
Prova scritta di Elementi di Fisica I - 18 Giugno 2009
Un’asta lineare, rigida, omogenea, di lunghezza L e densità lineare λ, è incernierata, senza attrito,
attorno ad un asse orizzontale, ortogonale al piano verticale in cui l’asta può muoversi (traccia O
in Fig.), distante 0.2 · L dall’estremo B dell’asta. L’asta, inizialmente orizzontale e ferma, viene
lasciata libera di ruotare e, dopo essere passata per la verticale per O, va ad urtare elasticamente,
con l’estremo A, una massa puntiforme m1 , quando si trova a formare un angolo θ◦ = 20◦ con la
verticale. Si chiede di determinare:
1. l’accelerazione angolare dell’asta durante il suo moto libero prima dell’urto;
2. la massima velocità angolare dell’asta durante il suo moto libero prima dell’urto;
3. la reazione vincolare (come vettore) esercitata in O sull’asta dal vincolo durante il suo moto
libero prima dell’urto;
4. la velocità angolare dell’asta e quella lineare del corpo m1 subito dopo l’urto;
5. l’angolo massimo (rispetto alla verticale) che raggiungerà l’asta dopo l’urto;
6. la gittata del corpo m1 , cioè la distanza, rispetto al punto dell’urto, alla quale intercetterà il
piano orizzontale passante per il punto dove è avvenuto l’urto.
[Valori numerici: L = 1.20 m; λ = 1.25 Kg/m; m1 = 500. g]
B
O
20
o
A
m1
• Utilizzare i simboli in tutti i passaggi e SOLO alla fine sostituire i valori numerici.
• Si usi il valore g = 9.81m/s2 e si diano i risultati con la precisione corrispondente.
• Inserire sempre le unitá di misura quando si considerano i valori numerici.
19 Fac. SMFN - CdL triennale in Matematica - a.a. 2006/2007
Prova scritta di Elementi di Fisica I - 18 Settembre 2007
Su un piano orizzontale liscio è fissato, tramite un fermo, l’estremo di una molla di lunghezza,
a riposo, l◦ = 40.0cm, costante elastica k = 4.0 · 102 N/m e massa trascurabile; all’altro estremo
della molla è attaccata una massa M2 = 2.0Kg, collegata, successivamente, ad una funicella ideale
che, passando su una carrucola di massa m e raggio r = 10.0cm, prosegue oltre il piano in direzione
verticale. All’altro estremo della funicella è attaccata una massa M1 = 4.0Kg.
Si chiede di determinare (considerando inizialmente m << M1 eM2 ):
1. la lunghezza totale le raggiunta dalla molla che assicura l’equilibrio all’intero sistema;
2. il periodo delle piccole oscillazioni del sistema ed il massimo del valore assoluto dell’accelerazione
di M1 durante questo regime dinamico;
3. i valori della tensione T1 applicata dalla funicella su M1 negli istanti in cui l’accelerazione del
sistema é massima (in valore assoluto).
4. Ripetere la domanda 2) nel caso in cui m = 600g non possa essere considerata trascurabile
rispetto a M1 e M2 e che la funicella non possa slittare nella gola della carrucola (cioè totale
aderenza fra funicella e carrucola).
5. Determinare le tensioni applicate dalla funicella su M1 e su M2 nel caso della domanda #4).
Osservazioni e suggerimenti:
• Si spieghino e si giustifichino le formule utilizzate.
• Si indichi con chiarezza il sistema di riferimento utilizzato.
• Usare possibilmente i simboli proposti nel testo.
• Utilizzare i simboli in tutti i passaggi e SOLO alla fine sostituire i valori numerici.
• Si usi il valore g = 9.81m/s2 e si diano i risultati con la precisione corrispondente.
• Inserire sempre le unitá di misura quando si considerano i valori numerici.
20 Fac. SMFN - CdL triennale in Matematica - a.a. 2010/2011
Prova scritta di FISICA I ed Elementi di Fisica I - 19 Luglio 2011
Un sistema rigido è composto da un cilindro omogeneo (raggio R = 2.00 cm, altezza h = 0.600 m
e densità relativa ρr = 7.80) a cui sono saldati (in modo radiale e simmetrico, v. Fig. non in scala) due
lastrine rettangolari di lunghezza L
=
20.0 cm e massa M
=
0.100 kg.
Il sistema, inizialmente fermo, è vincolato in un
piano verticale ad un asse OO’ verticale (coincim
dente con l’asse di simmetria del cilindro), che
O
vo
supporremo inizialmente senza attrito. Un corL
L
po (assimilabile ad un punto materiale) di masL
L
sa m si muove in un piano orizzontale, in diM
M
O
C
rezione ortogonale al centro della lastrina rettangolare di destra (in Fig.), di moto rettilineo uniO’
forme (almeno in vicinanza del sistema rigido),
con v◦ = 5.00 m/s. Si determini:
1. nel caso di urto elastico, il valore di m affinchè il punto materiale rimanga fermo immediatamente dopo l’urto;
2. il moto del sistema rigido immediatamente dopo l’urto elastico ed in particolare il valore dell’energia cinetica del sistema rigido immediatamente dopo l’urto;
Dopo mezzo giro del sistema rigido, la lastrina rettangolare (posizionata in Fig. inizialmente a
sinistra) andrà ad urtare, sempre elasticamente, la massa m ferma; si determini:
3. il moto del sistema rigido e della massa m dopo questo secondo urto ed il tempo intercorrente
fra il primo ed il secondo urto;
4. nel caso di urto anelastico (col valore di m determinato precedentemente), il moto del sistema
rigido dopo l’urto iniziale ed il bilancio energetico complessivo di tutto il sistema;
5. sempre nel caso di urto anelastico, il moto del sistema rigido dopo l’urto iniziale se esistesse
un attrito sull’asse di rotazione OO’ tale da generare un momento resistente costante pari a
−0.800 · 10−1 Nm durante il moto ed, in particolare, quante rotazioni farà il sistema rigido
prima di fermarsi;
6. sempre nel caso di urto anelastico, il moto del sistema rigido dopo l’urto iniziale se l’asse
di rotazione del sistema OO’ fosse costituito da un filo perfettamente elastico di costante di
torsione k = 0.315 Nm · rad−1 .
• Si trascurino gli effetti della gravità sul moto ed equilibrio della massa m; questo si può realizzare
utilizzando materiale ferromagnetico per m ed un opportuno campo magnetico verticale che
equilibri il peso di m.
• Si spieghino e si giustifichino le formule utilizzate.
• Si indichi con chiarezza il sistema di riferimento utilizzato.
• Usare possibilmente i simboli proposti nel testo.
• Utilizzare i simboli in tutti i passaggi e SOLO alla fine sostituire i valori numerici.
• Si usi il valore g = 9.81m/s2 e si diano i risultati con la precisione corrispondente.
• Inserire sempre le unitá di misura quando si considerano i valori numerici.
21 Fac. SMFN - CdL triennale in Matematica - a.a. 2010/2011
Prova scritta di FISICA I ed Elementi di Fisica I - 20 Settembre 2011
Una carrucola può essere schematizzata come due cilindri rigidi, omogenie, coassiali, saldati, di
raggio r e R, spessore s (v. Fig.) e densitá relativa ρr , libera di ruotare senza attrito attorno ad
un asse OO’ fisso. Nelle gole dei due cilindri possono avvolgersi, senza strisciare, due funi ideali
attaccate rispettivamente ad una massa M, libera di muoversi in direzione verticale, e ad una massa
m, posta su un piano orizzontale liscio. Al tempo t = 0 il sistema viene abbandonato all’effetto delle
forze applicate e si chiede di determinare:
s
1. l’accelerazione con cui si
muove M lungo la verticale;
2. la velocità acquistata da m
dopo 0.750 s di moto;
R
O’
s
r
m
O
3. il valore della tensione Tm applicata dalla fune su m e della
tensione TM applicata dalla
fune su M;
O
r
R
M
4. l’equazione di moto della carrucola sotto l’effetto di tutte le forze ad essa applicate;
5. nel caso in cui esista attrito (µ = coeff. d’attrito) fra m ed il piano orizzontale si ripetano le
valutazioni di cui ai punti precedenti.
Valori numerici: R = 2 · r = 20.0 cm; s = 10.0 cm; ρr = 2.70; m = 2.00 Kg; M = 5.00 Kg; µ =
0.200.
• Si spieghino e si giustifichino le formule utilizzate.
• Si indichi con chiarezza il sistema di riferimento utilizzato.
• Usare possibilmente i simboli proposti nel testo.
• Utilizzare i simboli in tutti i passaggi e SOLO alla fine sostituire i valori numerici.
• Si usi il valore g = 9.81m/s2 e si diano i risultati con la precisione corrispondente.
• Inserire sempre le unitá di misura quando si considerano i valori numerici.
22 Fac. SMFN - CdL triennale in Matematica - a.a. 2006/2007
Prova scritta di Elementi di Fisica I - 22 Gennaio 2008
Una carrucola (assimilabile ad un cilindro omogeneo di raggio 10.0 cm e massa M) puó ruotare,
senza attrito, attorno ad un asse orizzontale ed é sostenuta da un vincolo T passante per il suo
centro. Sulla gola della carrucola é posta una fune ideale (che trascina sempre la carrucola senza
slittare), al cui estremo A é attaccata una massa MA = 1.00 Kg, che risulta inizialmente appoggiata
al suolo (orizzontale); all’altro estremo B della fune é attaccata una massa MB = 2.50 Kg, che risulta
inizialmente sollevata dal suolo di un tratto h = 3.50 m. Si determini:
1. l’accelerazione del sistema e la velocitá con cui tocca il suolo la massa MB , nel caso in cui M
sia trascurabile rispetto a MA e MB ;
2. idem come al punto #1, ma nel caso in cui M = MA ;
3. la reazione vincolare in T, applicata al centro della carrucola, nei casi 1) e 2);
4. se al suolo, dove cade MB , fosse posta una molla ideale (posta in direzione verticale), di costante
elastica K = 1.00 · 104 N/m, determinare la compressione massima della molla nei casi 1) e 2).
Osservazioni e suggerimenti:
• Si spieghino e si giustifichino le formule utilizzate.
• Si indichi con chiarezza il sistema di riferimento utilizzato.
• Usare possibilmente i simboli proposti nel testo.
• Utilizzare i simboli in tutti i passaggi e SOLO alla fine sostituire i valori numerici.
• Si usi il valore g = 9.81m/s2 e si diano i risultati con la precisione corrispondente.
• Inserire sempre le unitá di misura quando si considerano i valori numerici.
23 Fac. SMFN - CdL triennale in Matematica - a.a. 2008/2009
Prova scritta di Elementi di Fisica I - 22 Settembre 2009
Una sfera omogenea di raggio R = 30.0 cm e densità relativa ρr = 2.75 è posta su un piano
scabro (µs = 0.40), inclinato di un angolo di 10◦ rispetto all’orizzontale; al suo centro (tramite un
opportuno taglio di dimensioni trascurabili) è applicata l’estremità di una molla ideale, di costante
elastica k = 103 N/m; l’altro estremo della molla è fissato ad un attacco solidale col piano inclinato.
Determinare:
1. l’allungamento della molla in condizioni di equilibrio del sistema;
2. il valore del modulo della forza di attrito esistente fra sfera e piano nelle condizioni di cui al
punto 1).
Spostato quasi-staticamente il centro di massa della sfera di 5.00 cm dalla sua posizione di equilibrio, si chiede di determinare:
3. il periodo delle oscillazioni del sistema quando viene abbandonato all’effetto delle forze applicate;
4. il valore massimo e minimo dell’accelerazione del centro di massa della sfera durante il moto
di cui al punto 3);
5. l’espressione della forza applicata dalla molla al centro di massa della sfera durante un’oscillazione
completa;
6. verificare che il valore dato di µs sia sempre adeguato a garantire le condizioni di rotolamento
puro per la sfera durante un’oscillazione.
Osservazioni e suggerimenti:
• Si spieghino e si giustifichino le formule utilizzate.
• Si indichi con chiarezza il sistema di riferimento utilizzato.
• Usare possibilmente i simboli proposti nel testo.
• Utilizzare i simboli in tutti i passaggi e SOLO alla fine sostituire i valori numerici.
• Si usi il valore g = 9.81m/s2 e si diano i risultati con la precisione corrispondente.
• Inserire sempre le unitá di misura quando si considerano i valori numerici.
24 Fac. SMFN - CdL triennale in Matematica - a.a. 2010/2011
Prova scritta di FISICA I ed Elementi di Fisica I - 23 Gennaio 2012
Con riferimento alla figura, una ”pendola” rigida è costituita da un’asta rigida, di lunghezza AB
= L = 1.50 m e massa M = 1.00 Kg, incernierata (senza attrito) su un asse orizzontale (ortogonale
al piano della figura), e traccia O in figura, con OA = 0.1 · L; un disco rigido, di raggio R = 0.1 · L
e densità superficiale σ = 7.07Kg/m2, è saldato (lungo un diametro e nel piano verticale contenente
OO’) all’estremità CB dell’asta, che, inizialmente, si trova in quiete in posizione verticale. Un corpo
puntiforme di massa m = M/2 e velocità costante v◦ è lanciato orizzontalmente al disco in C. Si
chiede di determinare:
A
1. il momento d’inerzia I◦ della ”pendola” rispetto all’asse
OO’ (notando che l’asse di rotazione del disco è parallelo
ad un suo diametro);
O
2. il verso della velocità v◦" di m immediatamente dopo l’urto
elastico con la ”pendola”;
3. il valore dell’angolo θM AX per il quale si abbia uno scarto
di 10−3 fra il sinθM AX e θM AX ;
θ
4. il valore di v◦ affinchè (nel caso di urto elastico) la ”pendola” oscilli, dopo l’urto, di moto armonico di ampiezza θM AX (cioè θM AX rappresenta il massimo valore dell’angolo che la ”pendola” formerà con la verticale dopo
l’urto (*);
5. il periodo delle piccole oscillazioni della ”pendola” e v◦" di
m dopo l’urto elastico.
m
6. la reazione vincolare in O immediatamente dopo l’urto
elastico.
C
vo
B
7. Ripetere le valutazioni nr. 3, 4, 5 nel caso di urto anelastico fra m e la ”pendola”.
(*) Si consiglia di fare una verifica energetica del valore θM AX trovato nel caso di urto elastico.
• Si spieghino e si giustifichino le formule utilizzate.
• Si indichi con chiarezza il sistema di riferimento utilizzato.
• Usare possibilmente i simboli proposti nel testo.
• Utilizzare i simboli in tutti i passaggi e SOLO alla fine sostituire i valori numerici.
• Si usi il valore g = 9.81m/s2 e si diano i risultati con la precisione corrispondente.
• Inserire sempre le unitá di misura quando si considerano i valori numerici.
25 Fac. SMFN - CdL triennale in Matematica - a.a. 2008/2009
Prova scritta di FISICA I ed Elem. di Fisica I - 25 Gennaio 2010
Un’asta rigida, omogenea, di lunghezza CB = 1.50 m e densità lineare λ = 1.00 g/cm, è vincolata
a ruotare, senza attrito, attorno ad un asse orizzontale posto ad una distanza OC = 1/3 CB, e forma
inizialmente un angolo di 20◦ con la verticale passante per il punto di sospensione O. Sul piano
orizzontale, liscio, tangente all’estremo B dell’asta, è posta una massa puntiforme m = 1/10 massa
dell’asta, inizialmente posta nel punto A tale che AB = CB. Si chiede di determinare:
1. la velocità v◦ che deve possedere la massa m nel punto A in modo che urti l’asta nel punto B,
quando l’asta venga rilasciata, da ferma, nella posizione iniziale (β◦ = 20◦ );
2. la velocità angolare dell’asta immediatamente prima dell’urto con la massa m;
3. il moto di m e dell’asta successivamente all’urto, sia nel caso di urto elastico che nel caso di
urto perfettamente anelastico (in questo caso si richiede anche l’analisi dell’energetica dei corpi
urtanti prima e dopo l’urto);
4. cosa cambierebbe nelle risposte precedenti se esistesse un coefficiente di attrito dinamico µ = 0.1
fra m ed il piano orizzontale.
C
O
βo
vo
A
m
B
• Utilizzare i simboli in tutti i passaggi e SOLO alla fine sostituire i valori numerici.
• Si usi il valore g = 9.81m/s2 e si diano i risultati con la precisione corrispondente.
• Inserire sempre le unitá di misura quando si considerano i valori numerici.
26 PROVA&SCRITTA&DI&FISICA1&per&il&Corso&di&Laurea&Triennale&in&MATEMATICA&
Esercizio&n.1&
Un#cilindro#pieno,#di#raggio#R#=#20.00#cm#e#massa#M#=#5.00#Kg,#è#libero#di#ruotare#attorno#al#suo#asse.#Su#di#
esso#è#avvolta#una#corda,#inestensibile#e#di#massa#trascurabile,##con#appeso#un#corpo#di#massa#m#=#2.00#Kg.##
Una#sbarra#orizzontale#di#lunghezza#L=1.00m#è#appoggiata#sul#cilindro#ad#¼#della#sua#lunghezza#dal#suo#
estremo#A#ed#è#libera#di#ruotare#attorno#ad#un#asse#perpendicolare#al#piano#della#figura#e#passante#per#
l’altro#estremo#B#(vedi#Fig.1).#Il#coefficiente#di#attrito#statico##e#dinamico#tra#la#sbarra#ed#il#cilindro#sono#
rispettivamente##
µs#=#0.30#e#µd#=#0.10##
Calcolare:#
a) Il#valore#minimo##Ms#della#massa#della#sbarra#che#mantiene#il#sistema#in#equilibrio#statico.#
Con#questo#valore#della#massa#Ms#calcolare##
b) La#forza#che#il#cilindro#esercita#sulla#sbarra#nel#punto#di#appoggio.#
c) La#forza#che#l’asse#di#rotazione#del#cilindro#esercita#sul#cilindro#
d) La#forza#che#l’asse#nel#punto#B#esercita#sulla#sbarra.#
Al#tempo#t=#0#s#,#si#raddoppia#la#massa#m#dell’oggetto#appeso#alla#corda,#che#diventa#m=4Kg,#ed#il#cilindro#
inizia#a#ruotare.#Calcolare:##
e)######L’accelerazione#angolare#del#cilindro#e#la#tensione#della#corda#
f)#######L’energia#cinetica#del#sistema#al#tempo#t#=#10#s#.#
g)#######Dopo#10#secondi,#quanta#energia#è#stata#dissipata#in#calore?#
#
Osservazioni#e#suggerimenti#
• Spiegare#e#giustificare#le#formule#utilizzate#
• Indicare#con#chiarezza#il#sistema#di#riferimento#usato#
• Usare#i#simboli#proposti#nel#testo#
• Utilizzare#i#simboli#in#tutti#i#passaggi#e#solo#alla#fine#sostituire#i#valori#numerici#con#le#loro#unità#di#
misura#
• Usare,#per#l’accelerazione#di#gravità,##il#valore#g=9,81#m/s2#e#si#diano#i#risultati#numerici#con#la#
precisione#corrispondente##
#
#
27 Lunedì'10'Febbraio'2014'
'
Corso'di'laurea'in'Fisica'6'Compito'di'Fisica1'–'Università'di'Firenze'
'
Esercizio'n.1'
'
Un'blocco'di'massa'm=5.00Kg'è'appoggiato'fermo'nel'centro'di'un'carrello'lungo'
L=1m'e'di'massa'M=20.00Kg,'come'mostrato'in'figura.''I'coefficienti'di'attrito,'
statico'e'dinamico,'tra'il'blocco'e'il'piano'del'carrello'sono,'rispettivamente,'
µs=0.8'e'µd=0.1'.''
Al'tempo't=0s'un'manovratore'spinge'il'carrello'con'una'forza'F'parallela'al'
piano.'Le'quattro'ruote'del'carrello'sono'di'massa'trascurabile.'
'
Si'calcoli:'
'
1)'la'forza'massima'con'la'quale'si'può'spingere'il'carrello'in'modo'che'il'blocco'
m'non'scivoli'sul'piano.'
2)'se'si'applica'una'forza'doppia'di'quella'calcolata,'dopo'quanto'tempo'il'blocco'
m'esce'dal'piano'del'carrello?'
3)'quanta'energia,'alla'fine,'è'stata'dissipata'in'calore?'
4)'qual'è'il'lavoro'compiuto'dalla'forza'F'?'
'
L
F
'
'
'
M
'
'
'
'
'
'
'
'
'
'
'
m
'
'
'
28 Lunedì'20'Gennaio'2014'
'
Corso'di'laurea'in'Fisica6Compito'di'Fisica1'–'Università'di'Firenze'
'
Esercizio'n.1'
'
Un'disco'omogeneo'di'raggio'esterno'R=30cm'e'massa'M=20Kg,'ruota'
liberamente'con'velocità'angolare'w0'='50s61'attorno'ad'un’asse'verticale'
passante'per'il'suo'centro.'
Un'secondo'disco'omogeneo'di'raggio'r=20cm,'di'massa'm=25Kg,'ruota'
liberamente'attorno'allo'stesso'asse.'Il'disco'piccolo'è'appoggiato'in'modo'quasi'
statico'(praticamente'fermo),'al'tempo't=0,'sul'disco'ruotante.'
A'causa'dell’attrito'tra'le'superfici'dei'dischi,'µd=0.3,'il'primo'rallenta'ed'il'
secondo'accelera'finché,'questi,'si'mettono'a'ruotare'alla'stessa'velocità'angolare.''
'
Si'calcoli:'
'
1)'la'velocità'angolare'finale'del'sistema'
2)'l’energia'totale'dissipata'in'calore''
3)'l’andamento'della'velocità'angolare'dei'due'dischi'in'funzione'del'tempo'
4)'il'tempo'che'i'due'dischi'impiegano'per'raggiungere'la'stessa'velocità'
angolare.''
'
'
Asse'di'rotazione'
'
'
'
r'
m=3Kg'
'
'
'
'
'
'
'
'
'
'
'
'
'
'
'
'
'
'
'
'
'
M=20Kg'
R'
'
29 Prova&scritta&di&FISICA&1.&&Università&di&Firenze8&12&Dicembre&2013812810&
&
Esercizio&n.1&
&
Una&sfera&di&raggio&R=21cm&e&massa&M=20Kg&è&contenuta&in&un&cilindro&di&raggio&R=21cm,&come&
mostrato&in&figura.&
Una&sferetta&più&piccola,&di&raggio&r=7cm&e&massa&m=5Kg&è&appoggiata&alla&sfera&e&alla&parete&del&
cilindro.&
Calcolare:&
&
1)&la&forza&che&la&sfera&piccola&esercita&sulla&parete&del&cilindro&e&sulla&sfera&grande.&
2)&la&forza&che&la&parete&laterale&del&cilindro&esercita&sulla&sfera&grande.&
&
Il&cilindro&è&poi&accelerato&con&accelerazione&a&verso&sinistra.&Supponendo&che&non&ci&sia&
scivolamento&tra&le&due&sfere,&calcolare&l’accelerazione&minima&affinché&la&sfera&piccola&passi&dalla&
parte&opposta.&
&
&
&
&
&
&
&
R&
a&
30 PROVA&SCRITTA&DI&FISICA1&per&il&Corso&di&Laurea&Triennale&in&MATEMATICA&
20&Settembre&2012&
&
Esercizio&n.1&
&
!!!!Un cilindro omogeneo di raggio R= 10,00 cm e massa M=15,00 Kg, viene messo in rotazione
attorno al suo asse con velocità angolare iniziale ω 0 = 100 s-1 e posto nell’angolo costruito con
due semipiani rugosi come mostrato in figura 1. Sapendo che il coefficiente di attrito dinamico tra il
cilindro ed i piani è µ = 0.12, si calcoli:
1. L’energia cinetica iniziale
2. Le reazioni vincolari dei due piani
3. La velocità angolare del cilindro in funzione del tempo
4. Il tempo di frenata
5. Il numero di giri che il cilindro compie prima di fermarsi
!
R = 10,00 cm
M = 15,00 Kg
ω 0 = 100,00 s-1
µ= 0.12
!
!!!!!!!!Fig.1&
&
Risposte:!
1) Ec=!375!J,!!
2) f1=!µ!Mg/!(1+µ2)!=!17.41!N!,!f2!=!µ!f1!=!2.09!N!!
3) ω(t)!=!@!(µ(1+ µ)/(1+µ2)!)!RMg!t!+!ω0 !
4) T!=!ω0 (1+µ2)/ µ(1+ µ)!RMg!=!51.29!s!
5) N!=!!3.83!giri!
&
31 Compito 17/1/2013
COMPITO SCRITTO DI FISICA 1 DEL CORSO DI LAUREA IN MATEMATICA
Esercizio 1)
Un blocco di legno di massa totale M= 5Kg è appoggiato su di un piano orizzontale con coefficienti
di attrito statico e dinamico pari a µs=0.8 e µd= 0.1, rispettivamente.
Un proiettile di massa m=10g è sparato nel legno con una velocità v=500m/s che forma un angolo
α=60° rispetto all’orizzontale. Nell’urto, completamente anelastico e che si può considerare
‘’istantaneo’’, il proiettile si conficca nel legno.
Si calcoli:
a)
b)
c)
d)
La velocità del blocco di legno immediatamente dopo l’urto
Quanta energia si è trasformata in calore nell’urto del proiettile con il legno
Lo spazio percorso dal blocco di legno (con proiettile) sul piano prima di fermarsi
Il tempo impiegato dal blocco per fermarsi
Sapendo che il proiettile è penetrato nel legno per 5 cm e che il suo moto può essere considerato
uniformemente accelerato, si calcoli:
e) Quanto tempo ha impiegato il proiettile per fermarsi nel legno
f) La reazione vincolare del piano sul blocco di legno durante la frenata del proiettile
g) La reazione vincolare del piano dopo la frenata del proiettile
m= 10g
v=500m/s
α = 60°
M=5Kg
Osservazioni e suggerimenti
• Spiegare e giustificare le formule utilizzate
• Indicare con chiarezza il sistema di riferimento usato
• Usare i simboli proposti nel testo
• Utilizzare i simboli in tutti i passaggi e solo alla fine sostituire i valori numerici con le loro
unità di misura
• Usare, per l’accelerazione di gravità, il valore g=9,81 m/s2 e si diano i risultati numerici con
la precisione corrispondente
32 Martedì(14(Gennaio(2014(
(
(
Corso(di(laurea(in(Fisica7Compito(di(Fisica1(–(Università(di(Firenze(
(
Esercizio(n.1(
(
Due(corpi(A(e(B,(rispettivamente(di(massa(m1=(5Kg(e(m2=(20Kg,(sono(legati(alle(
estremità(di(una(molla(con(costante(di(richiamo(elastica(K=(80(N/m(e(lunghezza(
a(riposo(l0=(2m(.(Il(tutto(è(appoggiato(su(un(piano(orizzontale(senza(attrito.(
(
Al(tempo(t=0(s(i(due(corpi(occupano(la(posizione(x1=(30cm(e(x2=(3m,(sono(fermi(e(
liberi(di(muoversi.((
(
Si(calcoli:(((
(
1)(l’energia(accumulata(nel(sistema(
2)(la(distanza(minima(tra(le(due(masse(durante(il(moto(del(sistema(
3)(la(posizione(e(il(moto(del(centro(di(massa,(in(funzione(del(tempo(
4)(la(frequenza(di(oscillazione(del(sistema(
5)(quale(condizione(deve(essere(soddisfatta(al(tempo(t=0,(affinché(le(due(masse(
non(si(urtino(durante(il(moto?(
6)(quale(deve(essere(il(coefficiente(di(attrito(statico(minimo(affinché(le(due(masse(
restino(ferme(nonostante(l’azione(della(molla?(
7)(Come(si(muovono(le(masse(se,(per(entrambe(le(masse,(µs=0.3(e(µd=0.1(?(
(
(
(
!
((((((((((((((((((((((((((((((m1=(5Kg(((((((((((((((((((((((((((((((((((((((((((((((((((((((
m2=(20Kg!
!
!
!
x(
0( (((((((((((((((((((((((((((((((((x1=(30cm((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((x2=(3m!
!
!
!
!
•!Si!spieghino!e!si!giustifichino!le!formule!che!vengono!utilizzate,!
•!si!indichi!con!chiarezza!il!sistema!di!riferimento!utilizzato,!
•!nei!limiti!del!possibile!si!usino!i!simboli!proposti!nel!testo,!
•!si!facciano!tutti!i!calcoli!con!i!simboli!e!si!sostituiscano!i!numeri!solo!per!
ottenere!il!risultato!finale,!
•!si!usi!g!=!9.81m/s2!e!si!diano!i!risultati!numerici!con!la!precisione!
corrispondente,!
•!si!tenga!conto!delle!unità!di!misura!nei!passaggi!con!i!valori!numerici.!
(
33 Fac. SMFN - CdL triennale in Matematica - a.a. 2011-2012
Prova scritta di Fisica I – 12 Febbraio 2013
Su un piano orizzontale liscio è fissato, tramite un fermo, l'estremo di una molla di lunghezza a
riposo l0=40.00 cm, costante elastica k=4.00 102N/m e massa trascurabile. All'altro estremo
della molla è attaccata una massa M2=2.00Kg, collegata ad una funicella di massa trascurabile
che tramite una carrucola di massa m e raggio r=10.00cm, sostiene la massa M1=4.00Kg.
Si chiede di determinare (considerando inizialmente m << M1eM2):
1) la lunghezza totale raggiunta dalla molla che assicura l'equilibrio all'intero sistema;
2) il periodo delle piccole oscillazioni del sistema ed il massimo del valore assoluto
dell'accelerazione di M1 durante questo regime dinamico;
3) i valori della tensione T1 applicata dalla funicella su M1 negli istanti in cui l'accelerazione del
sistema è massima (in valore assoluto).
4) Ripetere la domanda 2) nel caso in cui m = 600g non possa essere considerata trascurabile
rispetto a M1 e M2 e che la funicella non possa slittare nella gola della carrucola (cioè totale
aderenza fra funicella e carrucola).
5) Determinare le tensioni applicate dalla funicella su M1 e su M2 nel caso della domanda n.4.
Osservazioni e suggerimenti:
_ Si spieghino e si giustifchino le formule utilizzate.
_ Si indichi con chiarezza il sistema di riferimento utilizzato.
_ Usare possibilmente i simboli proposti nel testo.
_ Utilizzare i simboli in tutti i passaggi e SOLO alla fine sostituire i valori numerici.
_Si usi il valore g=9.81m/s2 e si diano i risultati con la precisione
corrispondente.
_ Inserire sempre le unità di misura quando si considerano i valori numerici.
34 “Diagramma di corpo libero” (5 “passi” )
1) Individuare il punto materiale (il corpo…) di cui si vuole studiare il moto.
2) Individuare tutti gli altri corpi che interagiscono con il punto materiale scelto e disegnare
tutte le forze che questi applicano al punto materiale. (…)
3) Scegliere un sistema di riferimento inerziale e, rispetto a questo sistema, scrivere in
componenti le forze di cui al passo 2 e le componenti della accelerazione.
(diagramma di corpo libero)
4) Applicare e risolvere F=ma
5) Controllare la soluzione: interpretare la risposta in termini fisici studiando i casi limite.
6) Solo a questo punto inserire nella soluzione i valori numerici con le loro unità.
Se ci sono piu’ punti materiali: ripetere per ogni punto materiale i passi 1-3 di cui sopra. Prima di
risolvere F=ma, tenere conto degli eventuali legami geometrici e/o cinematici tra i vari punti e del
“principio di azione e reazione” tra le forze che ciascun punto materiale applica agli altri punti
materiali considerati.
The free body diagram (also known as FBD) is a simplified representation of an object (the body), and the
forces acting on it. This body is called free because the diagram will show it without its surroundings; i.e. the
body is “free” of its environment.
In other words we consider the forces (and only the forces) acting on the object of our interest. The object is
seen as not connected to any other object – it is “free”.
35 CORSO DI LAUREA IN MATEMATICA - a.a. 2009-2010
Compito di FISICA 1 - 8-6-2010
Un sistema rigido é composto da due dischi omogenei, concentrici e solidali tra loro, rispettivamente di massa e raggio m1 , r1 e m2 , r2 . Il sistema é vincolato a ruotare intorno ad un
asse orizzontale, perpendicolare al piano dei dischi e passante per il loro centro. Un corda di
lunghezza l, perfettamente flessibile, inestensibile e di massa trascurabile, é avvolta intorno al
bordo di uno dei due dischi. All’estremitá libera della corda é attaccato un corpo di massa m,
assimilabile ad un punto materiale. Il sistema é lasciato partire da fermo, con la corda completamente avvolta. Trascurando per le domande 1 e 2 l’eventuale presenza di attrito sull’asse,
calcolare:
1) La velocitá angolare del sistema quando la corda si é svolta completamente (“al distacco”).
2) Il tempo di caduta.
In ambedue le domande, si facciano i calcoli sia per la corda avvolta intorno a r1 che avvolta
intorno a r2 e si commentino i risultati.
3) Dopo il distacco, il sistema continua a ruotare e si ferma dopo 80 giri per effetto dell’attrito
sull’asse. Calcolare il momento di attrito e come vengono modificati i risultati della prima
domanda.
Valori numerici: m1 = 20kg, m2 = 28.8kg, r1 = 5.4cm, r2 = 4.5cm, l = 2m, m = 10gr
Osservazioni e suggerimenti:
Si spieghino e si giustifichino le formule che vengono utilizzate.
Si indichi con chiarezza il sistema di riferimento utilizzato
Nei limiti del possibile si usino i simboli proposti nel testo.
Si cerchi di fare tutti i calcoli con i simboli e si sostituiscano i numeri solo per calcolare
il risultato finale.
• Si usi g = 9.81m/s2 e si diano i risultati numerici con la precisione corrispondente.
• Si tenga conto delle unitá di misura nei passaggi con i valori numerici.
•
•
•
•
Risultati Numerici:
1: ω1 ! ω2 = 2.59rad/s
2: t1 = 28.6s, t2 = 34.3s
3: M1 ! M2 = 0.390mJ, (ω1m ! ω2m ! 2.57rad/s)