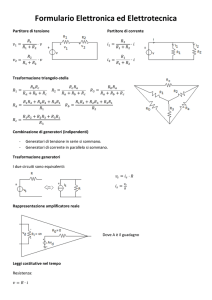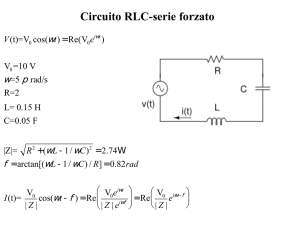
ESERCIZIO
Il circuito in figura funziona in regime sinusoidale. Determinare
Ø la corrente iL(t), applicando il teorema di Thévenin ai morsetti dell’induttore;
Ø la potenza reattiva QL assorbita dall’induttore L.
R1
R2
iL(t)
e(t)
e(t)=5 2 sen(wt)
i(t)= 2 2 sen(wt+p/2)
R1= R2= R3= 10 W
L= 5 mH; C= 1 mF
w=1000 rad/s
J(t)
L
C
R3
SVOLGIMENTO
Si utilizza il Metodo Simbolico (convenzione dei valori efficaci per i fasori).
R1
E
a
R2
c
ZC
ZL
R3
J
Calcolo dei fasori e delle impedenze:
E=5 V
J=2j A
ZL=jXL=jwL= j5 W
ZC=-jXC=-j/wC= -j1 W
b
Si cerca l’equivalente di Thévenin della rete “vista” dall’induttore L.
CALCOLO DELL’IMPEDENZA EQUIVALENTE Zab
R1
a
Zcb=R3//ZC=(-jR3XC)/(R3-jXC)= (-j10)/(10-j) W
= (-j10)/(10-j) W @ (0.10-j0.99) W
R2
Zcb
b
Zab=R1//(R2+Zcb)= R1(R2+Zcb)/[R1+R2+Zcb]
@ 10[10+(0.10-j0.99)]/[20+(0.10-j0.99)] W
= 10(10.10-j0.99)]/(20.10-j0.99) W
= (5.04-j0.24) W
CALCOLO DELLA TENSIONE A VUOTO
Si applica il principio di sovrapposizione degli effetti.
· Generatore di corrente “spento”
R2
R1
E
E0’
Applicando la regola del partitore di tensione si ha:
Zcb
E0’= (R2+Zcb)/(R1+R2+Zcb) E
@ [10+(0.10-j0.99)]/[20+(0.10-j0.99)] V
=(10.10-j0.99)/(20.10-j0.99) V = (0.50-j0.02) V
Generatore di tensione “spento”
·
R2
R1
Zcb
E0’’
J
La tensione cercata è pari alla caduta di
tensione sulla resistenza R1. Applicando la
regola del partitore di corrente, si ha:
E0’’ = R1I1= R1 [Zcb/(R1+R2+Zcb)] J
@ [10(0.10-j0.99)/(20.10-j0.99) 2j] V
= (0.98+j0.15) V
In sintesi:
E0= E0’+E0’’=(0.50-j0.02+0.98+j0.15) V = (1.48+j0.13) V = 1.49 ej0.09 V
Zab= (5.04-j0.24) W
Zab
Il fasore rappresentativo della corrente iL cercata è:
E0
IL= E0/(Zab+ZL) @ 1.49 ej0.09/(5.04-j0.24+j5) A
= 1.49 ej0.09/(6.93 ej0.76) A = 0.22 ej(0.03-0.76) A
= 0.21 e-j0.67 A
ZL
[-0.67rad®-38°]
Antitrasformando si ottiene iL(t)= 0.21 2 sen(1000t-0.67) A
~~~~~
La potenza reattiva assorbita dall’induttore è (avendo scelto, per i fasori, la convenzione
dei valore efficace):
QL=XLI2 @ 5×0.212 VAr = 0.22 VAr
QL= 0.22 VAr
A titolo di esempio, con riferimento alla quarta figura (che si riporta), si vogliono
rappresentare i fasori in gioco.
Zcb = (0.10-j0.99) W = e-j1.47 W
I
E
E=5V
E0’ = (0.50-j0.02) V = 0.50 e-j0.04V
R2
R1
E0’
Zcb
[1.56 rad @ -84°]
I = E/(R1+ R2+Zbc) @ 5/(20.10-j0.99) A = 0.25 ej0.05A
[0.05 rad @ 3°]
VR1 = R1I = 2.5 ej0.05V
VR2 = R2I = 2.5 ej0.05V
VZcb=ZcbI = 0.25 ej(-1.47+0.05) = 0.25 e-j1.42V
I
VZcb
[-1.42 rad @ -81°]
VR1,VR2
E0’
E
I fasori sono rappresentati fuori scala per favorire la
“leggibilità” del diagramma.