FENOMENI TRANSITORI NEI CIRCUITI RL
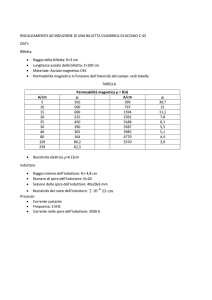
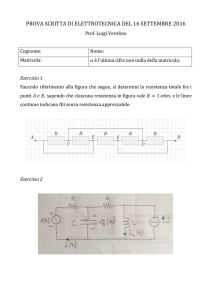
Il circuito qui rappresentato è formato da un’unica maglia con induttanza e resistenza in serie. Ha
come generatore di tensione una batteria con f.e.m. E. L’interruttore si chiude all’istante t=0 e
rimane in questo stato per un tempo infinito. Si vuole studiare l’evoluzione nel tempo delle
grandezze elettriche (tensioni, correnti).
Applicando la legge di Kirchhoff alla maglia si ottiene:
E = Ri + v L
e per la legge dell’induzione elettromagnetica: v L = L
di
, quindi si arriva all’equazione
dt
differenziale:
di
dt
nella quale l’incognita é rappresentata dalla corrente i(t), funzione del tempo.
E = Ri + L
−
t
L
R
(costante di tempo); A e B sono delle costanti da determinare che dipendono dalle condizioni
iniziali e finali del circuito.
Nel caso specifico la corrente i(t) é ovviamente nulla prima della chiusura. La corrente non subisce
discontinuità e pertanto i(0)=0 (più precisamente i(0+)=0 ).
Si può pensare l’induttore come un componente che tende a mantenere costante la corrente
che lo attraversa; esso mostra cioè una certa inerzia nei confronti delle rapide variazioni della stessa.
Quindi, dalla generica soluzione si ottiene:
i ( 0) = A + B = 0
Occorre un’altra equazione per determinare le due costanti. Con il circuito a regime, ovvero a
di
transitorio estinto 1, la corrente è costante: i (∞ ) = cost , pertanto
= 0 e la caduta sull’induttore
dt
di
é vL = L = 0 . In altri termini l’induttore equivale ad un cortocircuito per la corrente continua.
dt
La corrente finale è limitata dalla sola resistenza: E = Ri(∞ ) . Allora:
E
i (∞ ) = A =
R
E
E
Combinando le due equazioni si ottengono le costanti A e B: A = ; B = − A = − .
R
R
t
−
E E
L’espressione della corrente è in definitiva: i (t ) = − e L / R ed è rappresentata nel grafico
R R
seguente:
Si può dimostrare che la soluzione di tale equazione é del tipo: i (t ) = A + Be
1
τ
con
τ=
La funzione esponenziale e-x tende asintoticamente a zero per x → ∞, quindi il transitorio non si esaurisce mai
completamente; lo si può considerare praticamente estinto dopo un intervallo con durata di almeno 4 o 5 costanti di
tempo.
Più in generale, nei circuiti formati da un solo induttore e più resistori l’espressione della corrente in
un qualsiasi ramo è ancora i (t ) = A + Be
−
−
t
τ
(per la generica tensione sarà analogamente
t
v(t ) = C + De τ ). Le costanti dipendono anche in questi casi dalle condizioni iniziali e finali. Per
determinarle occorre esaminare con attenzione la topologia del circuito.
La costante di tempo si calcola come il rapporto tra l’induttanza e la resistenza equivalente “vista”
L
ai capi dall’induttore annullando i generatori indipendenti: τ =
.
Req
Ad es., si voglia determinare nel circuito seguente la tensione e la corrente sulla resistenza R2 :
vR 2 (t ) = C + De
−
t
τ
; iR 2 (t ) = A + Be
−
t
τ
(nell’ipotesi iL (0)=0 )
Analizzando lo schema si ottiene:
R2
v R 2 ( 0) = C + D = E
(poiché l’induttore inizialmente è un ramo “aperto”);
R1 + R2
vR 2 (∞) = C = 0 (l’induttore a regime cortocircuita la resistenza R2);
i R 2 ( 0) = A + B =
E
;
R1 + R2
i R 2 (∞ ) = A = 0 .
t
−
R2
eτ
R1 + R2
t
−
E
eτ
R1 + R2
L
(la resistenza
R1 R2
R1 + R2
equivalente vista ai capi dell’induttore è il parallelo delle due resistenze del circuito).
Una soluzione alternativa al problema consiste, ad esempio, nell’applicazione del teorema di
Thevenin. Si determina cioè il bipolo equivalente (generatore di tensione-resistenza) “visto” ai capi
dell’induttore. In tal modo si può calcolare la tensione ai capi dell’induttore e quindi della resistenza
R2 in parallelo.
Quindi: vR 2 (t ) = E
e
iR 2 (t ) =
con τ =