L’energia potenziale della forza elettrostatica
L’energia potenziale della forza di Coulomb
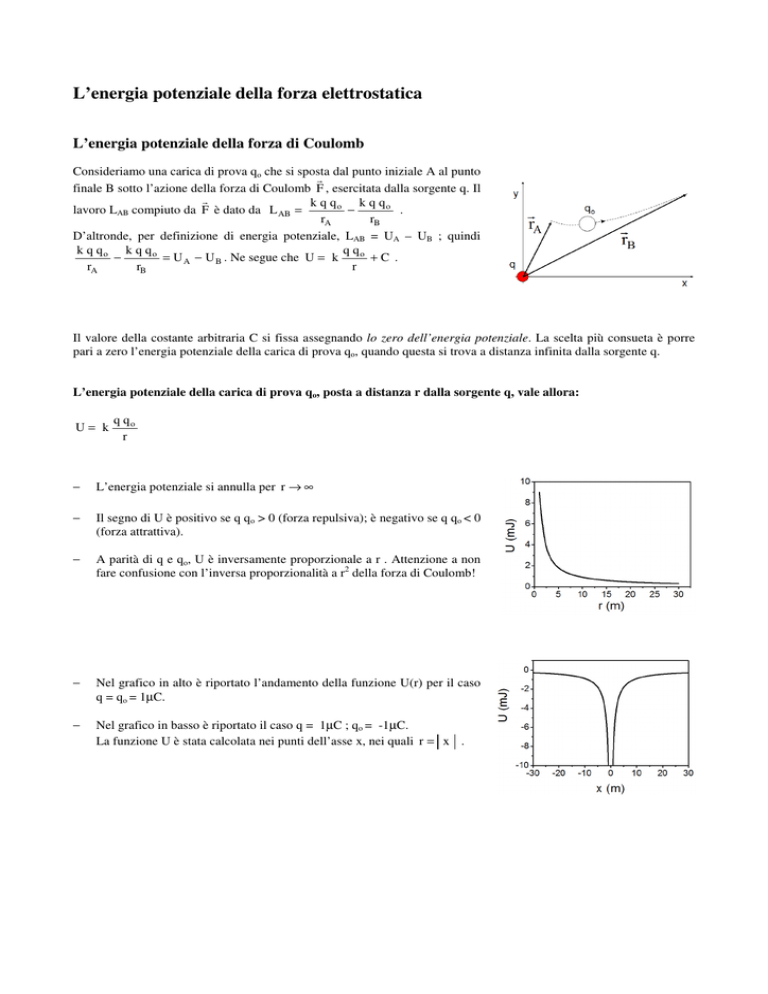
Consideriamo una carica di prova qo che si sposta dal punto iniziale A al punto
r
finale B sotto l’azione della forza di Coulomb F , esercitata dalla sorgente q. Il
r
k q qo k q qo
lavoro LAB compiuto da F è dato da L AB =
−
.
rA
rB
D’altronde, per definizione di energia potenziale, LAB = UA – UB ; quindi
q qo
k q qo k q qo
−
= U A − U B . Ne segue che U = k
+C .
r
rA
rB
Il valore della costante arbitraria C si fissa assegnando lo zero dell’energia potenziale. La scelta più consueta è porre
pari a zero l’energia potenziale della carica di prova qo, quando questa si trova a distanza infinita dalla sorgente q.
L’energia potenziale della carica di prova qo, posta a distanza r dalla sorgente q, vale allora:
U= k
q qo
r
−
L’energia potenziale si annulla per r → ∞
−
Il segno di U è positivo se q qo > 0 (forza repulsiva); è negativo se q qo < 0
(forza attrattiva).
−
A parità di q e qo, U è inversamente proporzionale a r . Attenzione a non
fare confusione con l’inversa proporzionalità a r2 della forza di Coulomb!
−
Nel grafico in alto è riportato l’andamento della funzione U(r) per il caso
q = qo = 1µC.
−
Nel grafico in basso è riportato il caso q = 1µC ; qo = -1µC.
La funzione U è stata calcolata nei punti dell’asse x, nei quali r = x .
L’atomo di Bohr
Bohr propose un modello semiclassico per l’atomo di Idrogeno, del quale riprendiamo in forma semplificata alcune
considerazioni valide per lo stato di minima energia (stato fondamentale).
L’elettrone che orbita nell’atomo di Idrogeno a distanza r dal
nucleo ha energia potenziale
U= −k
e2
r
e2
= 44 × 10 −19 J , dove ao = 0.53 ×10-10 m
ao
a
U
è il raggio di Bohr, si trova
= o . Il grafico di U/Uo in
Uo
r
funzione di r/ao è mostrato a fianco.
Ponendo U o = k
L’elettrone si muove in una buca di potenziale in regime di conservazione dell’energia meccanica. Come si vede
dal grafico, il livello di energia meccanica è ottenuto sommando l’energia cinetica K (positiva) all’energia
potenziale U (negativa).
1
m e v 2 , con me massa dell’elettrone,
2
Bohr ipotizzò che la traiettoria dell’elettrone nello stato fondamentale (cioè, lo
stato di energia meccanica più bassa) fosse una circonferenza di raggio ao.
Per determinare l’energia cinetica K =
r
r
In questa ipotesi, la dinamica dell’elettrone è descritta dalla II legge di Newton F = m e a che, proiettata in direzione
centripeta, dà F = m e a c . Sostituendo l’espressione della forza di Coulomb e dell’accelerazione centripeta, si trova
1
e2
e2
v2
e2
2
2
=
m
,
da
cui
m
v
=
k
e,
infine,
l’energia
cinetica
m
v
=
k
.
e
e
e
ao
2
a o2
ao
2 ao
L’energia meccanica dello stato fondamentale vale allora:
k
E mec = K + U =
e2
e2
e2
−
=−
2 ao ao
2 ao
; E mec = − 22 × 10 −19 J = − 13.6 eV
L’unità di misura eV (elettronvolt) è usata per misurare energie su scala atomica:
1 eV = 1.6 × 10-19 J
Energia di legame dell’elettrone nell’atomo di Idrogeno
Il minimo lavoro L che deve essere compiuto per estrarre un elettrone da un atomo si chiama energia di legame (o
di ionizzazione).
La regione in cui l’elettrone può muoversi è delimitata dalla
condizione che l’energia cinetica K sia positiva; quindi deve
essere:
K = Emec – U > 0 ; Emec > U
Nel grafico, questa condizione è soddisfatta nella regione
permessa marcata in giallo (in cui l’elettrone è confinato),
mentre non è soddisfatta nella regione proibita marcata in
rosso tratteggiato (alla quale l’elettrone non può accedere).
La minima energia meccanica per cui la regione permessa si
estenda a tutto lo spazio (elettrone libero) è EB = 0.
Il teorema dell’energia meccanica, applicato al processo di
ionizzazione dello stato A, si scrive allora:
L = EB - EA = -EA
Per l’elettrone nello stato fondamentale dell’atomo di
Idrogeno, L = 13.6 eV .
−
−
−
Se il lavoro compiuto sull’elettrone è minore di 13.6 eV, l’elettrone resta in uno stato legato; questo accade
quando l’elettrone passa dallo stato fondamentale a uno stato eccitato (per esempio, L = 10.2 eV nel passaggio
dallo stato 1s allo stato 2p; per il significato dei simboli 1s, 2p, si veda un manuale di chimica elementare).
Se il lavoro compiuto sull’elettrone è maggiore di 13.6 eV, l’energia eccedente si trasforma in energia cinetica
dell’elettrone estratto.
Se il lavoro compiuto sull’elettrone è uguale a 13.6 eV, l’energia cinetica finale è nulla.
Il lavoro di estrazione può essere compiuto in vari modi da una forza esterna. Per esempio, l’atomo potrebbe essere
urtato da un elettrone e la forza esterna sarebbe la forza di Coulomb tra elettroni; oppure, potrebbe essere investito
da un fotone e la forza esterna sarebbe la forza elettromagnetica. In quest’ultimo caso, L è pari all’energia hν del
fotone assorbito e il fenomeno prende il nome di fotoemissione.
Il principio di sovrapposizione per l’energia potenziale
L’energia potenziale U della carica di prova è la somma delle energie potenziali U1, U2… dovute alle singole sorgenti:
U = U1 + U 2 + ...
r
Infatti, la carica di prova si muove sotto l’azione della forza totale F che, per il principio di sovrapposizione, è la
r r
r
r r
somma delle forze F1 , F2 ... dovute alle singole sorgenti. Il lavoro di F è pari alla somma dei lavori di F1 , F2 ... ;
r
r r
quindi, anche l’energia potenziale di F sarà pari alla somma delle energie potenziali di F1 , F2 ...
Energia potenziale dell’elettrone in un solido
Quando un elettrone si trova in un solido, l’energia potenziale U è la somma delle energia potenziali U1, U2… dovute
alle cariche elettriche di tutti gli atomi del corpo. In pratica, si sovrappongono tante buche di potenziale poste a
distanza regolare (la distanza tra atomi, qui indicata col simbolo a) e si ottiene il profilo in figura.
− I minimi dell’energia potenziale corrispondono ai
centri degli atomi.
− Sul bordo, la funzione U si porta asintoticamente a
zero.
Se l’elettrone ha energia meccanica pari a
E1 : si trova in uno stato libero e può allontanarsi
dal solido;
E2 : è intrappolato nel solido;
E3 : è intrappolato in un atomo del solido e non può
passare a un altro atomo.
La meccanica quantistica dimostra però che non tutti i valori di energia
meccanica sono permessi. Per gli elettroni confinati nei solidi, la scala
delle energie è suddivisa in intervalli di valori permessi alternati a
intervalli vietati.
Gli intervalli permessi sono detti bande, denominate secondo lo schema a
fianco. Ciascuna banda può essere immaginata come sovrapposizione di
moltissimi livelli discreti, molto vicini in energia.
Come si vede confrontando i disegni, gli elettroni
dei livelli profondi sono intrappolati nei singoli
atomi, mentre quelli appartenenti alla banda di
valenza e alla banda di conduzione sono de
localizzati in tutto il solido.
Per comprendere come siano occupati i vari livelli, dobbiamo considerare il principio di esclusione di Pauli: in
ciascuno stato possono trovarsi al più due elettroni, con spin opposti. Immaginiamo allora di collocare gli elettroni nel
solido uno alla volta. I primi occuperanno i livelli profondi. Successivamente, vengono riempiti i livelli della banda di
valenza. Se restano elettroni da collocare, questi occuperanno la banda di conduzione.
Negli isolanti, la banda di valenza è completamente occupata e la banda di conduzione è vuota.
Nei metalli, la banda di conduzione è parzialmente occupata. Per esempio, nel rame ogni atomo contribuisce con 1
elettrone in banda di conduzione.
La meccanica quantistica spiega anche perché conduttori e isolanti abbiano diverse proprietà in elettrostatica: gli
elettroni della banda di valenza non si possono spostare. Qualitativamente, questo effetto è spiegato ancora dal
principio di Pauli: per spostare un elettrone, lo si deve collocare in un altro stato libero; ma non ci sono altri stati liberi
nella banda di valenza! Inoltre, è impossibile spostare l’elettrone nella banda di conduzione, perché servirebbe una
forza motrice che compia un lavoro molto grande. Al contrario, siccome la banda di conduzione è solo parzialmente
occupata, è facile trovare stati liberi perché l’elettrone si sposti.









