1 Trasmissione del calore Sorgente di calore: è un corpo in grado di

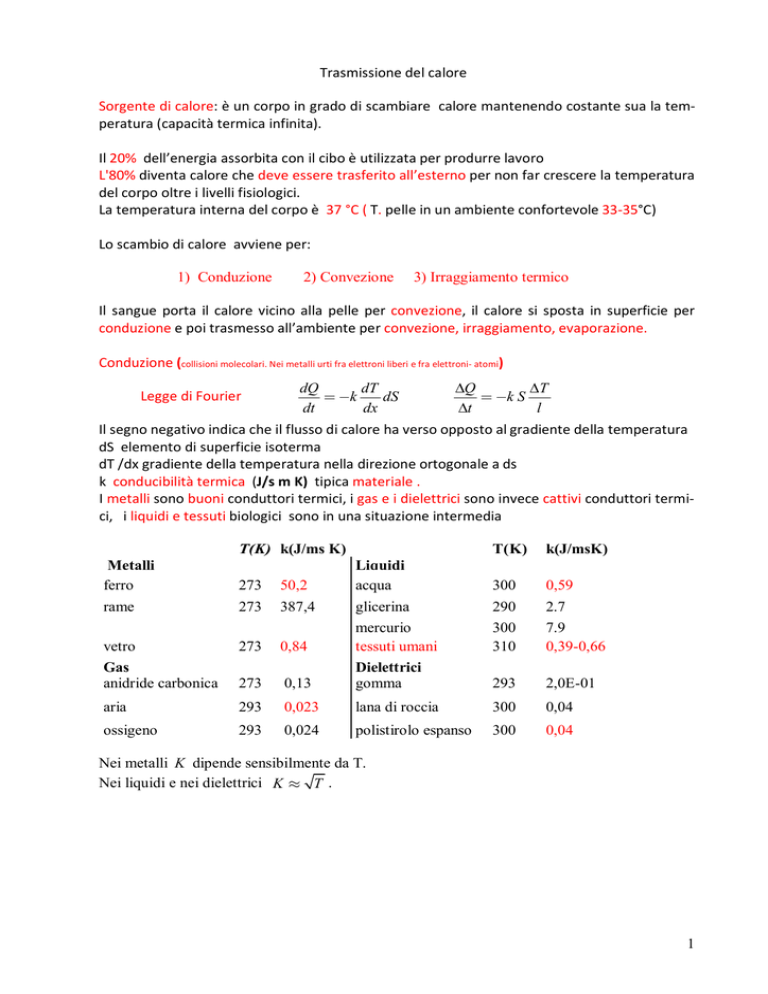
Trasmissione del calore
Sorgente di calore: è un corpo in grado di scambiare calore mantenendo costante sua la temperatura (capacità termica infinita).
Il 20% dell’energia assorbita con il cibo è utilizzata per produrre lavoro
L'80% diventa calore che deve essere trasferito all’esterno per non far crescere la temperatura
del corpo oltre i livelli fisiologici.
La temperatura interna del corpo è 37 °C ( T. pelle in un ambiente confortevole 33-35°C)
Lo scambio di calore avviene per:
1) Conduzione
2) Convezione
3) Irraggiamento termico
Il sangue porta il calore vicino alla pelle per convezione, il calore si sposta in superficie per
conduzione e poi trasmesso all’ambiente per convezione, irraggiamento, evaporazione.
Conduzione (collisioni molecolari. Nei metalli urti fra elettroni liberi e fra elettroni- atomi)
Legge di Fourier
dQ
dT
 k
dS
dt
dx
Q
T
 k S
t
l
Il segno negativo indica che il flusso di calore ha verso opposto al gradiente della temperatura
dS elemento di superficie isoterma
dT /dx gradiente della temperatura nella direzione ortogonale a ds
k conducibilità termica (J/s m K) tipica materiale .
I metalli sono buoni conduttori termici, i gas e i dielettrici sono invece cattivi conduttori termici, i liquidi e tessuti biologici sono in una situazione intermedia
T(K) k(J/ms K)
T(K)
k(J/msK)
300
0,59
290
300
310
2.7
7.9
0,39-0,66
0,13
glicerina
mercurio
tessuti umani
Dielettrici
gomma
293
2,0E-01
293
0,023
lana di roccia
300
0,04
293
0,024
polistirolo espanso
300
0,04
Metalli
ferro
273
50,2
rame
273
387,4
vetro
Gas
anidride carbonica
273
0,84
273
aria
ossigeno
Liquidi
acqua
Nei metalli K dipende sensibilmente da T.
Nei liquidi e nei dielettrici K  T .
1
Convezione
La convezione si manifesta nei fluidi quando il trasferimento di calore avviene con trasferimento di materia anche a grandi distanze in correnti convettive ( nell'atmosfera o nei mari).
Il fluido vicino alla sorgente si riscalda, aumenta di volume, aumenta la spinta di Archimede,
correnti ascensionali, masse fredde si avvicinano alla sorgente di calore.
*) Anomalia acqua:
In generale all’aumentare della temperatura, aumenta il volume e diminuisce la densità
L’acqua fa eccezione perché nell’intervallo da 4°C a 0°C la densità diminuisce.
Lago con temperatura atmosfera che scende da 25 °C verso 0 °C.
Da 25°C a 4°C la densità dell’acqua superficiale aumenta (normalmente) e quindi scende
verso il fondo facendo emergere acqua calda. Si creano correnti convettive che raffreddano
l’acqua del lago fino a 4 °C.
Da 4°C a 0°C la densità (contrariamente alla norma) diminuisce permettendo agli strati
superficiali a 4°C di rimanere in superficie evitando che l’acqua sottostante si raffreddi.
A 0°C l’acqua solidifica in ghiaccio con densità minore dell’acqua. Rimane in superficie
permettendo alla temperatura dell’acqua sottostante di rimanere attorno a 4°C.
densità
Densità aumenta
Acqua scende
Densità diminuisce
Acqua rimane in
superficie
0°C
4°C
2
Irraggiamento termico
Contrariamente alla conduzione e alla convezione, nell’irraggiamento la trasmissione del calore può avvenire anche senza un mezzo trasmissivo.
Legge di Stefan-Boltzmann La potenza complessivamente irraggiata da un corpo a temperatura T, sotto forma di uno spettro di o.e.m. a diverse λ è
q 
q
  S eT 4
t
Joule
sec
q
 0 il corpo perde energia e si raffredda
t
q
Se
 0 il corpo assorbe energia e si riscalda
t
σ costante Stefan-Boltzmann pari a 5.67 . 10 - 8 W/m2 K4
e emissività varia tra 0 e 1 e dipende dalle caratteristiche della superficie.
e = 1 (corpo nero)
e < 1 ma costante per le diverse λ il corpo è “grigio”.
Se
Se un corpo a T1 è immerso nell’ambiente a T2 omogenea, nell’ipotesi che (emissività) e ≈ coeff. di assorbimento
q 
q
  S e (T14  T2 4 )
t
Joule
sec
Se T1>T2 il flusso netto sarà da corpo a ambiente (+) il corpo si raffredda
Se T1<T2 il flusso netto sarà da ambiente a corpo (-) il corpo si riscalda
2
Esempio: Pelle T1=34°C con e ≈ a = 0,7 e S =1,5 m circondato da pareti stanza T2=15°C.
Q
 S e ( T14 T24 )5.67108 1.50,7(3044 2884 )120 W
t
Irradia
Spettro di radiazioni q ( ) emesso da corpo nero a varie Temperature.
La potenza complessivamente irraggiata q è l’area dello spettro
In ogni spettro c’è una  chiamata  max alla quale corrisponde una
Al diminuire di T , qmax ( ) diminuisce e max aumenta.
T1 > T2 > T3
3
Legge di Wien
Derivando e ponendo la derivata uguale a zero si ottiene che:
max  T  289, 7 105
Andamento dei
m K 
max degli spettri di emissione in funzione di T.
Evaporazione
w Lavoro necessario per separare una molecola dal liquido.
N A w  HV Calore molare di evaporazione. Energia necessaria per far evaporare una mole.
HV
  Calore latente di evaporazione. Energia necessaria per far evaporare 1 g
p.m
L’energia cinetica delle molecole di un liquido segue la distribuzione di Maxwell–Boltzmann
Ricordare V 2
T3 > T2 > T1
N
La velocità quadratica media a T1=30°C è 648 m/s
a T3= 100°C è 719 m/s.
Energia Cinetica
w
Solo le molecole che nella curva di distribuzione hanno energia cinetica maggiore di w possono separarsi dal liquido.
L'energia cinetica media delle molecole che rimangono diminuirà e anche la temperatura della
goccia di liquido diminuirà. Quando la goccia diviene più fredda della pelle assorbirà calore dal
corpo ristabilendo la distribuzione iniziale delle velocità delle molecole e facendo proseguire il
processo di evaporazione.
Gli uomini (foglie) mantengono costante la temperatura corporea facendo evaporare acqua
dalla pelle.
Sostanze come l’Ossigeno hanno una w cosi bassa che anche a temperatura ambiente tutte le
molecole hanno energia cinetica maggiore di w e quindi l’ossigeno è gassoso.
n.molecole
Ta
w
4
Sostanze come l’acqua hanno una w e quindi una HV
cui a temperatura ambiente sono liquide.
(10.670 cal/mol a 20°C) per
Hv
L’acqua ha Hv = Calore molare di evaporazione di 10670 cal/mole. (20°C)
10467 cal/mole. (35°C)
L’acqua ha λ = Calore latente di evaporazione di circa 10670/18 = 593 cal/gr.( 20°C)
10467/18 = 582 cal/gr.( 35°C)
Con l’aumentare della temperatura il Calore latente di evaporazione diminuisce.
Per l’acqua fra 0-100 °C è dato da λ = 606.5 – 0.695 t. cal/g
Esempio
Una mole di acqua (18 g) evaporando a 35°C porta con sé 10467 calorie. 1 Kg di
tessuto ( acqua) perdendo 10467 calorie si raffredda di
Q  mcs T
T 
Q
10467

 10, 4C
mcs 1000 g 1 cal
gK
5
GAS IDEALI
I parametri adottati per individuare lo stato termodinamico del gas sono p,V,T, massa (n)
Un gas ideale ha le seguenti caratteristiche:





le molecole siano puntiformi, indistinguibili
interagiscono tra loro e con le pareti solo attraverso urti perfettamente elastici ;
non esistono forze di interazione a distanza tra le molecole del gas ( no energia potenziale); no liquefazione.
In conseguenza di ciò:
il gas ideale non può essere liquefatto per compressione;
il calore specifico è costante, ( non dipende da T).
Un gas reale, lontano cioè da condizioni di liquefazione, bassa pressione e alta temperatura,
si comporta come un gas ideale
1° Legge dei gas ideali - Boyle ( Isoterma)
Mantenendo costante la Temperatura si trova che
PV  cos t (T )
P1 V1 T  P2 V2 T
1
P
Energia interna costante. T = cost.
1
P-V piano di Clapeyron
v
2° Legge dei gas ideali - Gay_Lussac ( Isobara)
In una trasformazione a pressione costante, al variare della temperatura il volume varia secondo la relazione
V  V0 T
V (T )  V0 (1   T )
P
V0 è il volume a T=273,15 K (es: di una mole)
∆T in Kelvin
α è il coefficiente di dilatazione dei gas =1/273,15

V
T V0
V
variazione di volume relativa a V0 per una variazione di 1 K
∆Q = n Cp ∆T
VB-VA = V0 α (TB - TA)
3° Legge dei gas - Gay_Lussac ( Isocora)
In una trasformazione a volume costante, variando la temperatura la pressione varia secondo la relazione
P
p  p0  T
p (T )  p0 (1   T )
P0 è la pressione a T=273,15 K
(0°C )
V
6
 
1
273,16
per tutti i gas
∆Q = n CV ∆T
4° Legge dei gas Avogadro
Volumi uguali di gas diversi, nelle stesse condizioni di T e P, contengono lo stesso numero
di molecole. Come dire, noti PVT , ricavo n indipendentemente dal gas
Gas 1
T, P
Gas 2
T, P
Ovvero
una mole di gas diversi alla stessa T e P occupa lo stesso volume.
una mole a T0 (273,15 K) e PA( 1 atm) ( STP) occupa un VM = 22,4 litri
mole = 6,022 × 1023 molecole
Condizioni standard (STP), cioè T = 273.15 K (0°C), P = 1 atm Vm = 22.414 L mol 1 .
Condizioni ambiente standard (SATP), T = 298.15K (25°C), P = 1 bar Vm = 24.790 L mol 1
Le leggi sui gas ideali sono integrate in un’unica legge dei gas ideali in equilibrio
PV  nRT
Significato di R
Se P = cost
PV  nRT
P V  R
n = 1 ; ∆T=1 ; Avremo
R è il lavoro compiuto da una mole di gas che espande il suo volume a pressione costante
in seguito a una ∆T=1.
Se pensiamo che la pressione costante sia 1 atm= 101300 Pa
da
V  V0 (1  T )
V V0  V  V0 T
dove  
1
273,15
V0 volume di una mole a 273,15 K e 1 atm, cioè 22, 4 103 m3
R  P V  P  V0 T  101300 
1
 22, 4 103  8,31 J / mol K  1, 98 cal / mol K
273,15
Se V contiene un miscuglio di gas, si chiama pressione parziale del gas1, la pressione
P1 che il gas1 eserciterebbe se occupasse da solo tutto il volume V.
La legge di Dalton stabilisce sperimentalmente che la pressione del miscuglio è la
somma delle pressioni parziali.
PV
 n1RT
1
PV
 n2 RT
2
(P1 +P2 +...)  V= (n1  n2  ...) RT
PV
 n3 RT
3
PV= (n1  n2  ...) RT
Se nel miscuglio gassoso è contenuto un vapore saturo, la pressione totale è la somma delle pressioni parziali dei gas più la
pressione del vapore saturo.
7
Trasformazione Isoterma ( reversibile) T = cost. U  0
Nella Isoterma, una parete è diatermica a contatto con sorgente a T e una parete è mobile
SorgenteT
T
T  cos t. U  0
dal 1° Principio Q CB =LCB
Si espande/comprime il gas ( in condizioni quasi statiche e senza attrito con la pressione in equilibrio con quella
esterna Pest ) compensando il lavoro scambiato assorbendo/cedendo calore in modo da mantenere costante T .
In una espansione Isoterma Reversibile CB
VB
VB
QCB  LCB   P(V ) dV  
VC
VC
nRT
V
P
dV  nRTLn B  nRTLn C
V
VC
PB
0
PCVC  PBVB
Il lavoro è l’area sottesa dalla curva ed è  se percorsa da C a B è  se percorsa da B a C.
A P(v) posso sostituire l’espressione che deriva dalla eq. gas perfetti in quanto la trasformazione è Reversibile e ogni punto della curva è un punto di equilibrio
P
C
Da C a B Espando
LCB > 0
QCB > 0
assorbo calore per T cost
T2
SorgenteT
T
Da D a A Comprimo
LDA < 0
QDA < 0
Cedo calore
V=cost Assorbo calore, Riscaldo aumenta la Pres.
T1
B
A
D
V
V=cost Cedo calore, Raffreddo
quindi P diminuisce
Nella trasformazione chiusa reversibile ACBDA, il lavoro netto è l’area racchiusa dal rettangoloide. Sarà > 0 se il ciclo è percorso in senso orario e < 0 in caso contrario.
Se durante il ciclo viene prodotto lavoro netto L > 0 assorbendo e cedendo calore da un certo numero di sorgenti il ciclo è detto termico e il
dispositivo si chiama macchina termica.
Variazione di Entropia in un sistema Non isolato che si espande isotermicamente
B
B
B
VB
Q
L
pdV
dV
V


  nR
 nR ln B  0
VC
T
T C T
V
VC
C
C
S  
8
Trasformazione Adiabatica
Reversibile (∆Q = 0)
∆Q = 0
U  LCB
Nella lenta espansione adiabatica CB, il lavoro compiuto dal gas ( > 0) non viene compensato
da calore assorbito per cui T diminuisce e U  0 .
Nella lenta compressione adiabatica BC, il lavoro compiuto sul gas (< 0) non viene compensato
da calore ceduto per cui T aumenta e U  0 .
Dal 1 principio Q=0  U+L =0
ma U  n cV dT e L =pdV
pdV
P
n cV
differenziando equazione dei gas perfetti pV  nRT,
ncV dT
pdV  Vdp  nRdT
Sostituisco il dT ricavato dal 1 principio e risolvo
R
PdV (1  )  VdP  0
divido per PV
cV
ncV dT  pdV  0
(1 
da cui
dT  
C
PV=cost
PV   cos t
A
B
R dV
dP
)

cV V
P
PV   cos t
Legge di Poisson  
cp
1
cv
γ >1 per cui la curva ha una pendenza maggiore della isoterma
Cercando la relazione fra V e T, (dovrò sostituire P)
Da 1 principio
ncV dT  pdV  0
Da equazione gas perfetti p 
ncV dT 
nRT
dV  0
V
nRT
V
cV dT dV

0
R T
V
VC 1
VB 1
Per calcolare il Lavoro nella trasformazione adiabatica CB
T V  1  cos t
TB  TC
V  1 


LCB  U CB  n cV (TB  TC )  ncV TC  C  1
VB 



pV
c
c
pV
LCB  n cV ( B B  C C )   V ( PBVB  PCVC )   V ( PBVB  PCVC )
nR
nR
R
cP  cV
9
Trasformazioni Isocore
Reversibile
V=cost. ∆L=0
P
TC
sorgente
TA
V
Il gas, inizialmente a TA, è in un recipiente rigido con parete diatermica a contatto con sorgente TC.
Aumentando la temperatura, aumenta la pressione.
In questo caso dq diventa un differenziale esatto
Da 1 principio LAC  0 Q  U  ncV (TC  TA )
da Legge gas
Q  ncV
PV  nRT
T
T
V
T
  A  C  cos t
nR P PA
PC
TC  PC
T
P
TA  PA
T
P
T
( PC  PA )
P
In una trasformazione isocora il calore scambiato corrisponde alla variazione di energia interna.
Dal 1 principio  Q  dU  dL  ncv dT  pdV
B  Q 
S   

A
 T rev
In generale
T 
V 
S  n cV log  B   n R log  B 
 TA 
 VA 
Per isocora si ottiene
T 
S  n cV log  B 
 TA 
Entalpia nella isocora
dH  dU  pdV  Vdp
= dU+Vdp
10
Trasformazione Isobara
miche
reversibile
∆L≠0 ∆Q≠0
P = cost
∆U≠0
Reazioni chi-
P
Sorgente TB
P
TA
TB
V
Il gas inizialmente è a TA , la parete diatermica è a contatto con sorgente a TB. Sulla parete
mobile P = cost ( es: Patm.).
1 Principio U  Q  L
Q  ncP (TB  TA )
* p = cost
dove
uso c p
U  ncV (TB  TA )
L  p (VB VA )  nR (TB  TA )
Legge gas
** VB 
nRTB
nRTA
VA 
p
p
Delle tre relazioni solo due sono indipendenti perché devono soddisfare il 1 Principio,
Infatti, l’espressione L avrei potuto ottenerla facendo la differenza fra la prima e la seconda relazione.
La relazione
Q  L  U
dice che nella espansione isobara AB, il calore assorbito, in
parte viene impiegato per compiere lavoro positivo sull’ambiente e in parte viene impiegato
per aumentare l'energia interna ∆U.
Diversamente dalla isocora (dove ∆Q = ∆U) ora ∆Q è maggiore di ∆U
Entalpia H=U+pV
Differenziando H si ottiene
dH  dU  pdV  Vdp *
dH   Q  Vdp
Espressione Differenziale di H
dH è un differenziale esatto
dp  0
dH  dQ
In una trasformazione a pressione costante, il calore scambiato corrisponde alla variazione della Entalpia.
∆U e ∆H sono grandezze simmetriche che rappresentano il calore scambiato rispettivamente a volume costante e a pressione costante.
11
Variazione Entropia nella isobara reversibile
S |P  
 Q |p
B
T 
dT
  nc p ·  nc p ·ln  B 
A
A
T
T
 TA 
B
cp è il calore specifico molare a pressione costante
Ovvero utilizzando l’espressione generale
Dal 1 principio  Q  dU  dL  ncv dT  pdV
B  Q 
S   

A
 T rev
T 
V 
S  n cV log  B   n R log  B 
 TA 
 VA 
12