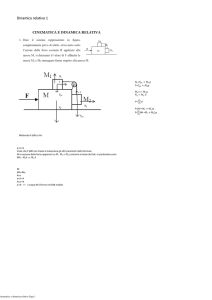
CINEMATICA E DINAMICA RELATIVA
1. Dato il sistema
rappresentato in figura,
M1
completamente privo di attriti, ed in moto sotto
F
l’azione della forza costante F applicata alla
M
M2
massa M, si determini il valore di F affinché le
masse M1 e M2 rimangano ferme rispetto alla massa M.
2. Uno studente per non bagnarsi in una giornata di pioggia, inclina l’ombrello di
30° in avanti rispetto alla verticale (direzione lungo la quale cade la pioggia).
Sapendo che lo studente si muove con velocità V di modulo 5 m/s, determinare
il modulo v della velocità delle gocce di pioggia rispetto al suolo.
3. Un fagiolo sferico di massa m = 30 g descrive un
moto circolare uniforme in un piano orizzontale di
uno scolapasta emisferico di raggio R = 20 cm . Se
esso possiede una velocità v = 1 m s determinare
la quota h a cui si trova rispetto al fondo dello scolapasta.
4. Una giostra ruota intorno al proprio asse con velocità angolare ω costante. Un
bambino si trova al centro della giostra ed al tempo t0 = 0 s lancia una pallina
in direzione radiale con velocità iniziale v′0 = 30 m s . Calcolare velocità ed
accelerazione della pallina per un osservatore inerziale non solidale con la
giostra.
5. Un aeroplano di massa pari a 200 tonnellate è in volo da Sud verso Nord lungo
un meridiano con velocità, relativa ad un osservatore terrestre, pari a
v = 900 km h . Si determinino modulo, direzione e verso della forza di
Coriolis
agente
sull’aeroplano
quando
si
trova
alla
latitudine
di
λ = 30° considerando sia il caso di latitudine nord (emisfero australe), sia il
caso di latitudine sud (emisfero boreale).
6. L’automobile A in figura sta percorrendo lo
svincolo circolare di raggio R mantenendo il
modulo della velocità v costante. L’automobile
B sta invece viaggiando sull’autostrada alla
stessa velocità dell’automobile A . Determinare
il vettore velocità v ′ di B in un sistema di
riferimento S ′ solidale con l’automobile A e
dimostrare che quando l’automobile B sta
oltrepassando l’asse x del sistema di riferimento assoluto essa è nulla
indipendentemente dalla posizione di A sullo svincolo.
7. Una piattaforma ruota con velocità angolare costante ω0 = 10 rad s ; si
consideri un sistema di riferimento solidale con essa avente origine nel centro
ed un altro con la stessa origine ma solidale con il suolo. Un cubetto è legato
tramite una fune inestensibile e di peso trascurabile di lunghezza l = 1.5 m al
centro della giostra e ruota anch’esso alla velocità ω0 ; tra fune e cubetto non vi
è attrito. Misurando la tensione della fune con un dinamometro si osserva che
essa vale T = 15 N . La piattaforma viene quindi rallentata fino ad una velocità
ω = 2 rad s
e
mantenuta poi
costante
a
questo
valore.
Calcolare
l’accelerazione e la velocità del cubetto dal sistema solidale con la piattaforma
e la massa del cubetto.