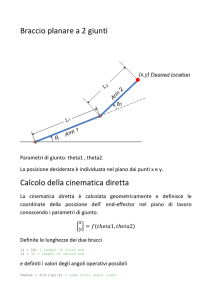
Dinamica relativa 1
T
=
T=
T
a=
F=(M +
F= (M +
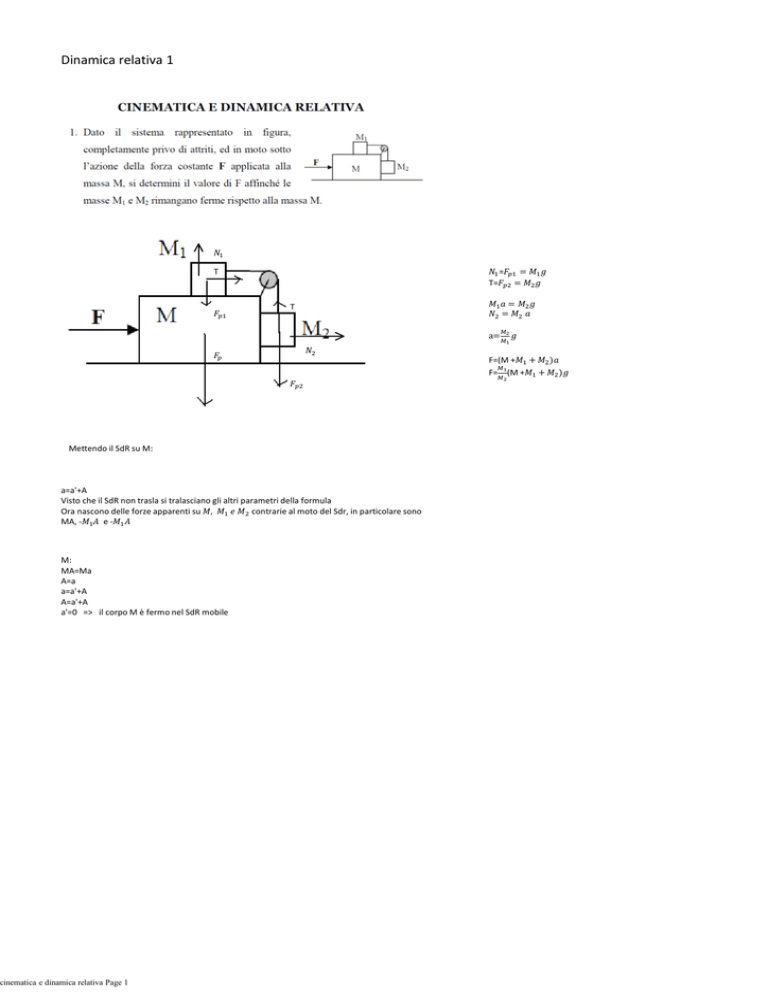
Mettendo il SdR su M:
a=a'+A
Visto che il SdR non trasla si tralasciano gli altri parametri della formula
Ora nascono delle forze apparenti su
contrarie al moto del Sdr, in particolare sono
MA, e-
M:
MA=Ma
A=a
a=a'+A
A=a'+A
a'=0 => il corpo M è fermo nel SdR mobile
cinematica e dinamica relativa Page 1
Dinamica relativa 2
v'=10 m/s
cinematica e dinamica relativa Page 2
Dinamica relativa 3
h=R-R sinθ=R
cinematica e dinamica relativa Page 3
Dinamica relativa 4
Una giostra ruota intorno al proprio asse con velocità angolare ω costante. Un
bambino si trova al centro della giostra ed al tempo
=0 s lancia una pallina
in direzione radiale con velocità iniziale
=30 m s . Calcolare velocità ed
accelerazione della pallina per un osservatore inerziale non solidale con la
giostra.
R= costante
V= = 0
A=0
Sposto il SdR fisso nel centro O', perchè non influise nè sulla velocità nè
sull'accelerazione
Y
Y'
X'
O=O'
R
Y
O
X
?V,a
=
=
=
=
=
(t)=
=
+
a=
cinematica e dinamica relativa Page 4
X
N
Dinamica relativa 5
Un aeroplano di massa pari a 200 tonnellate è in volo da Sud verso Nord lungo
un meridiano con velocità, relativa ad un osservatore terrestre, pari a
v=900 km h . Si determinino modulo, direzione e verso della forza di
Coriolis agente sull’aeroplano quando si trova alla latitudine di
λ =30°considerando sia il caso di latitudine nord (emisfero australe), sia il
caso di latitudine sud (emisfero boreale).
λ
λ
W
E
ω=
T=tempo di rotazione attorno all'asse (periodo)
T=24h=24*60*60 s
Nel caso il moto fosse nell'altro senso la
cinematica e dinamica relativa Page 5
sarebbe entrante
S
Dinamica relativa 6
L’automobile A in figura sta percorrendo lo svincolo circolare di raggio R mantenendo il modulo della velocità v costante.
L’automobile B sta invece viaggiando sull’autostrada alla stessa velocità dell’automobile A. Determinare il vettore
velocità v′ di B in un sistema di riferimento S′ solidale con l’automobile A e dimostrare che quando l’automobile B sta
oltrepassando l’asse x del sistema di riferimento assoluto essa è nulla indipendentemente dalla posizione di A sullo
svincolo.
V=costante
V=
?
X'
Y'
P
Y
=
O'
velocità di A
=
O
=
-
cinematica e dinamica relativa Page 6
X
Dinamica relativa 7
Una piattaforma ruota con velocità angolare costante 0 ω =10 rad s ; siconsideri un sistema di riferimento solidale con
essa avente origine nel centroed un altro con la stessa origine ma solidale con il suolo. Un cubetto è legato tramite una
fune inestensibile e di peso trascurabile di lunghezza l =1.5 m al centro della giostra e ruota anch’esso alla velocità 0
ω ; tra fune e cubetto non vi è attrito. Misurando la tensione della fune con un dinamometro si osserva che
essa vale T =15 N. La piattaforma viene quindi rallentata fino ad una velocità ω =2 rad s e mantenuta poi costante a
questo valore. Calcolare l’accelerazione e la velocità del cubetto dal sistema solidale con la piattaforma
e la massa del cubetto.
cinematica e dinamica relativa Page 7
m/s
Dinamica relativa 8
Una torre alta h=100 m è situata all'equatore terestre. Una massa m viene lasciata cadere dalla cima della torre. Si
calcoli di quanto la massa si scosterà dalla direzione verticale quando sarà giunta al suolo ed in he direzione si sarà
spostata.
N
X'
Y'
R
h
O
W
E
N
S
S
W
Bisognerebbe mettere R+h, ma h<<R e quindi si può tralasciare
y'(t)=
=
Per sapere quando la massa arriva al suolo pongo
y'(t)=h
t=
cinematica e dinamica relativa Page 8
-
x'(t)=