SNT1-2-4_Esercitazione_Elettricita_e_Circuiti

ESERCITAZIONE ELETTRICITA’ E CIRCUITI – ESEMPI GUIDATI
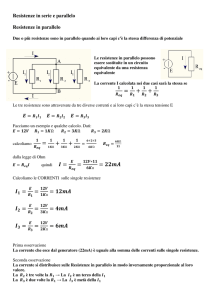
Tre resistenze in serie
Un circuito è formato da tre resistenze collegate in serie a una batteria da 24,0 V. La corrente nel circuito è di
0,0320 A. Sapendo che R1 = 250,0 , R2 = 150,0  , trovare:
a. il valore di R3;
R1
b. la differenza di potenziale ai capi di ciascuna resistenza.
Descrizione
In figura è mostrato il circuito. Osserviamo che attraverso
ciascuna resistenza passa la medesima corrente I = 0,0320A
I
R2
V
R3
I
Strategia
a. Innanzitutto, possiamo ottenere la resistenza equivalente
del circuito utilizzando la legge di Ohm: R eq =
V
I
.
Poiché le resistenze sono in serie, sappiamo anche che Req = R1 + R2 + R3 ,
e da questa relazione possiamo ricavare l'unica incognita R3.
b. Possiamo quindi calcolare la differenza di potenziale ai capi di ciascuna resistenza
utilizzando ancora la legge di Ohm, V = R ∙ I
Soluzione
a.
1. Utilizziamo la legge di Ohm per trovare la resistenza equivalente
R eq =
V
I
=
24,0V
0,0320A
= 750
2. Uguagliamo Req alla somma delle resistenze e ricaviamo R3
Req = R1 + R2 + R3
R 3 = R eq – R1 – R 2 = 750  − 250,0  − 150,0  = 350 
b.
3. Utilizziamo la legge di Ohm per determinare la
differenza di potenziale ai capi di R1
V1 = R1 ∙ I = (250,0 ) ∙ (0,0320A) = 8,00V
4. Troviamo la differenza di potenziale ai capi di R2
V2 = R 2 ∙ I = (150,0 ) ∙ (0,0320A) = 4,80V
5. Troviamo la differenza di potenziale ai capi di R3
V3 = R 3 ∙ I = (750,0 ) ∙ (0,0320A) = 11,2V
Osservazioni
Maggiore è la resistenza, maggiore è la relativa differenza di potenziale. Inoltre, la somma delle singole
differenze di potenziale è 8,00 V + 4,80 V + 11,2 V = 24,0 V, come deve essere.
Problema
Trovare la potenza dissipata su ciascuna resistenza.
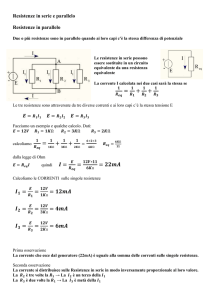
Tre resistenze in parallelo
Considera un circuito con tre resistenze, R1 = 250,0 , R2 = 150,0  e R3 = 350,0 , collegate in parallelo con
una batteria da 24,0 V. Trovare:
a. la corrente totale fornita dalla batteria;
b. la corrente che passa attraverso ciascuna resistenza.
I1
I
Descrizione
In figura è mostrato il collegamento in parallelo delle resistenze V
con la batteria. In questo caso, ciascuna resistenza ha, ai suoi capi,
la medesima differenza di potenziale.
R1
I2
R2
I3
R3
I
Strategia
V
a. Possiamo trovare la corrente totale utilizzando la relazione I =
dove Req è calcolata mediante la formula
1
Req
=
1
R1
+
1
R2
+
,
Req
1
R3
b. Per ciascuna resistenza la corrente è data dalla legge di Ohm, I =
V
Req
.
Soluzione
a.
1. Troviamo la resistenza equivalente del circuito:
1
Req
=
1
R1
+
1
R2
+
1
R3
=
1
250,0 
R eq =
+
1
150,0 
1
0.01352 −1
+
1
350,0 
= 0,01352 −1
= 73,96 
b.
2. Utilizziamo la legge di Ohm per trovare la corrente totale
V
I=
V
Req
3. Calcoliamo I1 utilizzando I1 = R con V = 24,0 V
I1 =
4. Ripetiamo il calcolo precedente per le resistenze 2 e 3
I2 =
1
I3 =
V
R1
V
R2
=
=
=
24V
73,96 
24V
250,0 
24V
150,0 
= 0,325 A
= 0,0960 A
= 0,160 A
V
24V
=
= 0,0686 A
R 3 350,0 
Osservazioni
Come si vede la resistenza minore è attraversata dalla corrente maggiore e la somma delle tre correnti fornisce
la corrente totale I
I = I1 + I2 + I3 = 0,325A + 0,0960A + 0,160A = 0,325A
Problema
Trovare la potenza dissipata su ciascuna resistenza
Tre resistenze
Tre resistenze, R1 = 150,0 , R2 = 250,0  e R3 = 350,0 , sono
collegate come in figura e alimentate da una batteria da 24,0 V. Trovare:
a. la corrente totale fornita dalla batteria;
b. la differenza di potenziale (d.d.p.) ai capi di R2 (VAC)
c. la differenza di potenziale (d.d.p.) tra i punti A e B
R1
d. la corrente che passa attraverso ciascuna resistenza.
I1
R3
A
I2
R2
I
C
V
B
Strategia
a. Per determinare la corrente totale fornita dalla batteria è necessario
trovare la resistenza equivalente totale. Perciò bisogna esaminare
ogni coppia di resistenze per vedere se sono in serie o in parallelo e sostituire alla coppia la resistenza
equivalente. Procedendo in questo modo si arriverà ad una unica resistenza equivalente e la corrente totale
sarà data dalla legge di Ohm: I =
V
Req
b. la d.d.p. VAC ai capi di R2 è data dalla corrente I (che è la corrente totale precedentemente calcolata) che
passa nella resistenza R2
c. poiché il punto A è a potenziale minore del punto C (a causa della caduta di potenziale causata dalla
resistenza R2), la d.d.p. tra i punti A e B è data dalla differenza tra la d.d.p. della batteria, V, e la d.d.p. ai
capi di R2.
d. la corrente che passa in R1 è data dalla legge di Ohm: I1 =
V1
R1
=
VAB
R1
dove VAB è la d.d.p. ai capi di R1
il calcolo della corrente in R3 è analogo.
Soluzione
a.
Per trovare la resistenza equivalente iniziamo con l’esaminare R1 ed R2; queste non sono in serie, poiché nel
punto A è inserita anche la resistenza R3 e quindi la corrente che passa in R1 non è la stessa di quella che passa
in R2; non sono in parallelo perché il potenziale del punto A è lo stesso per entrambe, ma il potenziale del
secondo estremo di R1 (punto B) non è lo stesso del potenziale del secondo estremo di R2 (punto C), poiché tra i
punti B e C è inserita la batteria.
Esaminiamo ora R2 ed R3; per lo stessa analisi precedente non sono né in serie né in parallelo.
Infine R1 ed R3; queste due resistenze hanno un loro estremo al potenziale A e l’altro estremo al potenziale B,
quindi sono sottoposte alla stessa differenza di potenziale VAB e quindi sono in parallelo. Possiamo ridisegnare
la figura per rendere più evidente questo fatto:
I1
I2
I2
R2
R1
I1 A
A
R2
I
C
V
B
R3
R1
C
R3
B
I
V
La resistenza equivalente del parallelo di R1 ed R3 è data da:
R AB =
(150,0 ) ∙ (350,0 )
R1 ∙ R 3
=
= 105 
R1 + R 3 (150,0 ) + (350,0 )
A
Ed il circuito può essere disegnato come nella figura a fianco;
ora le resistenze RAB ed R2 sono evidentemente in serie, e la resistenza
equivalente a questa serie è data da :
R eq = R AB + R 2 = (105,0 ) + (250,0 ) = 355 
R2
C
RAB
Quindi nel circuito finale (figura sottostante):
B
la corrente totale è:
I
C
Req
V
I=
V
Req
=
24V
355
= 67,6 ∙ 10−3 A
b.
la d.d.p. ai capi di R2 è data dalla legge di Ohm:
VAC = V2 = R 2 ∙ I = (250,0 ) ∙ (67,6 ∙ 10
−3
A) = 16,9V
c.
mentre la d.d.p. tra i punti A e B è:
VAB = VAC + V = 24,0V − 16,9V = 7,1V
d.
infine la corrente in R1 è:
I1 =
V1
VAB
7,1V
−3
=
=
= 47,3 ∙ 10 A
R1
R1
150,0 
I3 =
V3
VAB
7,1V
−3
=
=
= 20,3 ∙ 10 A
R3
R3
350,0 
E la corrente in R3 è
Osservazione
Si noti come la somma delle due correnti I1 e I2 è pari alla corrente totale I (conservazione della carica)
I
V