LICEO SCIENTIFICO-LINGUISTICO “A. M. DE CARLO” GIUGLIANO IN CAMPANIA(NA)
ANNO SCOLASTICO 2013/2014
LICEO SCIENTIFICO-LINGUISTICO “A.M.DE CARLO”
GIUGLIANO IN CAMPANIA (NA)
ANNO SCOLASTICO 2013-2014
PROGRAMMAZIONE ANNUALE DEL DIPARTIMENTO DI MATEMATICA E FISICA
FINALITA’ GENERALI
I percorsi liceali devono fornire allo studente gli strumenti culturali e metodologici per una
comprensione approfondita della realtà, affinchè egli si ponga, con atteggiamento razionale,
creativo, progettuale e critico, di fronte alle situazioni, ai fenomeni e ai problemi, ed
acquisisca conoscenze, abilità e competenze sia adeguate al proseguimento degli studi di ordine
superiore, all’inserimento nella vita sociale, nel mondo del lavoro, sia coerenti con le
capacità e le scelte personali.
Al termine di un percorso liceale, l’alunno deve aver conseguito i seguenti:
OBIETTIVI TRASVERSALI
Osservare con spirito critico e capacità di analisi gli accadimenti della vita reale.
Porsi problemi, formulare ipotesi e prospettare soluzioni.
Organizzare con rigore logico le proprie conoscenze, mettendole in relazione con altre già
acquisite e applicandole in situazioni nuove, per interpretare fenomeni e per risolvere
situazioni problematiche.
Sviluppare ragionamenti di tipo induttivo-deduttivo secondo le regole della logica e del
corretto ragionare.
Cogliere le relazioni tra lo sviluppo delle conoscenze scientifiche e quello del contesto
umano, storico e tecnologico.
Acquisire autonomia di pensiero e capacità di comunicare con chiarezza ed efficacia le
proprie idee.
Lavorare in gruppo con senso di responsabilità nel rispetto dei compiti, dei ruoli e delle
competenze individuali.
Adoperare i metodi, i linguaggi e gli strumenti informatici in situazioni di studio, di
ricerca e di lavoro.
OBIETTIVI DISCIPLINARI
MATEMATICA
Acquisire
conoscenze
su
livelli
più
elevati
di
astrazione
e
formalizzazione, attraverso l’analisi di strutture algebriche complesse
(campo reale e campo complesso) e l’uso di un linguaggio sempre più
specifico e corretto
Acquisire il linguaggio, i contenuti e i procedimenti caratteristici della
disciplina in riferimento alle quattro aree tematiche prescritte dalle
Indicazioni Nazionali per il nuovo Liceo Scientifico.
Saper individuare i concetti fondamentali e le strutture di base che
unificano
le
varie
branche
della
Matematica
e
ne
determinano
l'organizzazione complessiva.
Acquisire il metodo induttivo-deduttivo, avendo chiara consapevolezza del
valore sia dei procedimenti induttivi e della loro utilità nell'analisi,
nella risoluzione di situazioni problematiche, sia dei procedimenti
deduttivi e della loro utilità nella costruzione di modelli, di teorie e di
sistemi assiomatici.
Comprendere le capacità di previsione e di interpretazione della Matematica
nei riguardi dei fenomeni non solo naturali, ma anche economici, sociali e
della vita reale in genere.
Saper affrontare situazioni problematiche di varia natura adottando
strategie economiche e soddisfacenti.
Saper utilizzare metodi, strumenti e modelli matematici in situazioni
diverse dai contesti specifici di apprendimento.
Pagina 1 di 21
LICEO SCIENTIFICO-LINGUISTICO “A. M. DE CARLO” GIUGLIANO IN CAMPANIA(NA)
FISICA
ANNO SCOLASTICO 2013/2014
Comprendere i procedimenti caratteristici dell’indagine scientifica che si
articolano in un continuo rapporto tra costruzione teorica e attività
sperimentale.
Saper utilizzare strumentazione scientifica e sistemi automatici di calcolo
e di elaborazione dati.
Saper reperire informazioni, rielaborarle e comunicarle con linguaggio
scientifico.
Acquisire l’abitudine all’approfondimento, alla riflessione individuale e
all’organizzazione del lavoro personale e di gruppo.
Acquisire consapevolezza delle potenzialità e dei limiti delle conoscenze
scientifiche
Cogliere le relazioni tra l’avanzamento delle conoscenze scientifiche e
quelle del contesto umano, storico e tecnologico.
Comprendere il ruolo fondamentale, in tutti gli ambiti dell’attività umana,
del metodo scientifico come strumento irrinunciabile di costruzione e di
evoluzione delle conoscenze scientifico-tecnologiche.
OBIETTIVI SPECIFICI
PRIMO BIENNIO-NUOVO ORDINAMENTO
FISICA
CLASSE PRIMA
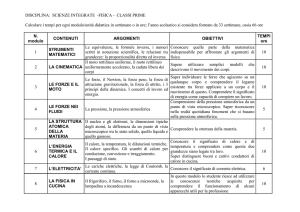
CONTENUTI
Le grandezze
Strumenti
matematici
La misura
Le forze
CONOSCENZE
ABILITA’
Spiegare il concetto di definizione
operativa di grandezza fisica.
Conoscere il Sistema Internazionale
di Unità di misura.
Enunciare (anche non rigorosamente)
le ultime definizioni del S.I. delle
unità
di
misura
meccaniche
di
lunghezza
(metro),
massa
(chilogrammo) e tempo (secondo).
Distinguere le grandezze fisiche, e
relative unità di misura, di base o
fondamentali da quelle derivate.
Definire la densità di una sostanza.
Utilizzare le diverse notazioni per
le grandezze fisiche (scientifica,
multipli e sottomultipli) sapendole
trasformare da una all’altra.
Calcolare la massa se è nota la
densità e il volume o inversamente
calcolare il volume se è nota la
densità e la massa.
Definire e calcolare la pendenza di
una retta nel piano cartesiano.
Enunciare
le
equazioni
tra
due
grandezze direttamente proporzionali
o in relazione lineare e saperle
rappresentare graficamente.
Riconoscere da tabelle di dati se due
grandezze sono tra loro direttamente
proporzionali o in relazione lineare
Conoscere le caratteristiche degli
strumenti di misura.
Saper valutare gli errori sia nelle
misure
dirette
che
in
quelle
indirette di una grandezza fisica.
Sapere attribuire l’errore assoluto
ad una misura diretta sapendo la
sensibilità dello strumento usato.
Saper
spiegare
le
cifre
significative.
Saper effettuare semplici operazioni
matematiche, impostare proporzioni e
definire le percentuali.
Saper leggere e interpretare formule
e grafici.
Saper applicare le proprietà delle
potenze.
Saper definire le operazioni tra
vettori.
Conoscere l’effetto delle forze.
Saper che
le forze sono forze di
contatto e azione a distanza.
Definire trigonometricamente (usando
Usare correttamente gli strumenti e i
metodi di misura delle forze.
Operare
con
grandezze
fisiche
scalari e vettoriali.
Determinare la risultante di più
forze: graficamente con la poligonale
Pagina 2 di 21
Saper calcolare l’errore relativo (e
percentuale) da quello assoluto e
viceversa.
Saper calcolare, in casi semplici,
l’errore assoluto o relativo di una
misura indiretta applicando le leggi
di propagazione degli errori.
Saper esprimere il risultato di una
misura con il corretto uso di cifre
significative.
Calcolare il valore medio di una
serie di misure.
Calcolare l’errore massimo di una
serie di misure.
LICEO SCIENTIFICO-LINGUISTICO “A. M. DE CARLO” GIUGLIANO IN CAMPANIA(NA)
L’equilibrio dei
solidi
L’equilibrio dei
fluidi
Laboratorio di
Fisica
ANNO SCOLASTICO 2013/2014
solo cateti e ipotenusa) tangente,
seno e coseno di un angolo acuto.
Definire, non rigorosamente, il peso
di un corpo in prossimità della
superficie terrestre.
Distinguere i concetti di massa e
peso di un corpo, sapendo passare da
una
all’altro
e
viceversa
(non
ricorrendo
all’accelerazione
di
gravità).
Definire il chilogrammo-peso ed in
sua funzione il newton.
Definire le caratteristiche della
forza d’attrito (statico e dinamico).
Spiegare approssimativamente il
concetto di forza elastica di una
molla allungata o accorciata (cenno
al principio di azione e reazione).
Definire e calcolare la costante
elastica di una molla.
o
analiticamente
sommando
le
componenti lungo due assi ortogonali.
Calcolare lati o angoli incogniti di
un triangolo rettangolo se sono noti
due lati o un lato e un angolo.
Calcolare la componente di una forza
lungo una generica direzione.
Calcolare il valore della forza-peso
Determinare la forza di attrito al
distacco e in movimento.
Utilizzare la legge di Hooke per il
calcolo delle forze elastiche.
Concetti di punto materiale e corpo
rigido.
Equilibrio del punto materiale e del
corpo rigido Equilibrio su un piano
inclinato.
Momento di una forza e di una coppia
di forze.
Saper classificare le leve.
Analizzare situazioni di equilibrio
statico.
Analizzare i casi di equilibrio.
stabile, instabile e indifferente.
Determinare le componenti del peso di
un corpo fermo su un piano inclinato,
parallela o perpendicolare al piano
stesso, la forza parallela al piano
inclinato che tiene il corpo fermo e
la reazione del piano sul corpo.
Risolvere problemi con un corpo fermo
su un piano inclinato aventi come
incognita una delle quattro forze
precedenti o il peso del corpo
l’angolo d’inclinazione del piano.
Determinare l’equilibrante di più
forze.
Risolvere problemi con aste rigide in
equilibrio, appoggiate o incernierate
in un punto, aventi come incognita
una
forza
o
il
suo
punto
di
applicazione.
Saper
calcolare
la
pressione
determinata dall’applicazione di una
forza e la pressione esercitata dai
liquidi.
Applicare le leggi di Pascal, di
Stevino e di Archimede nello studio
dell’equilibrio dei fluidi.
Analizzare
le
condizioni
di
galleggiamento dei corpi.
Comprendere il ruolo della pressione
atmosferica.
Gli stati di aggregazione molecolare.
La definizione di pressione e la
pressione nei liquidi.
La legge di Pascal e la legge di
Stevino.
La spinta di Archimede.
Il galleggiamento dei corpi.
La pressione atmosferica e la sua
misurazione.
Misure dirette e indirette delle principali grandezze fisiche introdotte.
Ricerca e/o verifica sperimentale di alcune leggi e principi fondamentali
introdotti.
Uso del Personal Computer per:
l’elaborazione analitica e grafica dei dati sperimentali; la stesura di
relazioni, anche in forma di ipertesti; la simulazione di esperimenti
difficilmente realizzabili in laboratorio;la ricerca scientifica in rete
telematica.
Pagina 3 di 21
LICEO SCIENTIFICO-LINGUISTICO “A. M. DE CARLO” GIUGLIANO IN CAMPANIA(NA)
FISICA
CLASSE SECONDA
CONTENUTI
Moto rettilineo
uniforme
Moto rettilineo
uniformemente
accelerato
Moto curvilineo
ANNO SCOLASTICO 2013/2014
CONOSCENZE
ABILITA’
Descrivere il moto rettilineo uniforme.
Definire la posizione di un corpo in moto
rettilineo e il suo spostamento tra due
posizioni in due distinti istanti.
Definire la velocità media in un generico
moto rettilineo.
Enunciare la legge tra posizione e tempo di
un corpo in moto rettilineo uniforme e
saperla rappresentare graficamente.
Riconoscere la relatività dei concetti
di quiete e moto di un corpo rispetto a
un
dato
sistema
di
riferimento
e
definirne la traiettoria.
Calcolare il modulo della posizione (in
m/s
e
km/h),
riconoscendone
il
significato nel grafico posizione-tempo.
Calcolare lo spostamento o l’intervallo
di tempo, nota la velocità media.
Risolvere,
analiticamente
o
graficamente, problemi con uno o due
corpi in moto rettilineo uniforme.
Risolvere problemi con un corpo in moto
uniformemente accelerato.
Risolvere problemi con due corpi, uno in
moto rettilineo uniforme e l’altro in
moto uniformemente accelerato
Risolvere
problemi
con
un
corpo
inizialmente fermo in caduta libera o
con un corpo a generica altezza e
velocità iniziale verticale.
Descrivere il moto rettilineo uniformemente
accelerato di un corpo.
Definire
(anche
non
rigorosamente)
la
velocità
istantanea,
riconoscendone
il
significato nel grafico posizione-tempo.
Definire
l’accelerazione
media
in
un
generico moto rettilineo, calcolarne il
modulo, riconoscendone il significato nel
grafico velocità-tempo.
Enunciare
le
leggi
velocità-tempo
e
posizione-tempo
di
un
corpo
in
moto
uniformemente accelerato, rispetto ad un
sistema
di
riferimento
arbitrariamente
scelto,
e
saperle
rappresentare
graficamente.
Riconoscere il significato dello spazio
percorso nel grafico velocità-tempo .
Enunciare la legge velocità-posizione di un
corpo in un moto uniformemente accelerato.
Definire
(anche
non
rigorosamente)
l’accelerazione istantanea, riconoscendone
il significato nel grafico velocità-tempo.
Definire il vettore posizione di un corpo
in moto curvilineo e il vettore spostamento
tra due posizioni in due distinti istanti.
Definire il vettore velocità media di un
corpo tra due punti di una traiettoria
curvilinea.
Definire
(anche
non
rigorosamente)
il
vettore velocità istantanea di un corpo in
un punto di una traiettoria curvilinea,
indicandone la direzione tangenziale.
Pagina 4 di 21
Risolvere esercizi grafico-numerici sul
moto curvilineo relativi ai vettori
velocità
accelerazione,
o
le
sue
componenti
LICEO SCIENTIFICO-LINGUISTICO “A. M. DE CARLO” GIUGLIANO IN CAMPANIA(NA)
ANNO SCOLASTICO 2013/2014
Definire il periodo ed enunciare la sua Risolvere problemi cinematici sul moto
relazione con il modulo della velocità circolare uniforme
(periferica o tangenziale).
Definire la frequenza ed enunciare la sua
relazione con il periodo.
Definire
il
radiante
ed
enunciare
la
relazione tra un angolo alla circonferenza
espresso in radianti e il corrispondente
arco.
Definire la velocità angolare ed enunciare
le sue relazioni con il periodo, la
frequenza e la velocità periferica
Definire il vettore accelerazione media di
un corpo tra due punti di una traiettoria
curvilinea.
Definire
(anche
non
rigorosamente)
il
Moto circolare
vettore accelerazione istantanea di un
uniforme
corpo in un punto di una traiettoria
curvilinea.
Distinguere il tipo di moto, rettilineo
accelerato
o
decelerato,
o
curvilineo
accelerato, uniforme o decelerato in base
all’angolo
tra
i
vettori
velocità
istantanea e accelerazione istantanea
Riconoscere la dipendenza tra variazione in
direzione
del
vettore
velocità
e
accelerazione centripeta e variazione in
modulo del vettore velocità e accelerazione
tangenziale.
Enunciare la direzione, il verso ed il
modulo dell’accelerazione centripeta.
Enunciare la direzione, il verso ed il
modulo dell’accelerazione tangenziale.
Enunciare il primo principio della dinamica Applicare il secondo principio della
o principio d’inerzia.
dinamica alla risoluzione di
problemi
Enunciare
il
secondo
principio
della con un corpo soggetto ad una o più
dinamica
forze.
Definire il newton.
Applicare il secondo principio della
Enunciare il terzo principio della dinamica dinamica alla risoluzione di problemi
o principio di azione e reazione.
con un sistema di corpi collegati.
Riconoscere forze di azione e reazione tra Risolvere problemi con un corpo in moto
coppie di corpi.
su
un
piano
inclinato
liscio
Spiegare la relazione tra peso, massa e inizialmente in generica posizione e
accelerazione di gravità.
velocità iniziale.
Trovare l’accelerazione di un corpo su un Determinare la forza di attrito radente
Principi della
piano inclinato liscio
dinamico agente su un corpo a contatto
dinamica
Spiegare la dinamica del moto circolare di un piano (orizzontale, inclinato o
uniforme individuando la forza centripeta verticale) o tra due corpi a contatto
come risultante delle forze agenti sul tra loro.
corpo.
Applicare il secondo principio della
dinamica alla risoluzione di problemi
con un corpo soggetto a più forze
compreso l’attrito.
Applicare il secondo principio della
dinamica alla risoluzione di semplici
problemi con un corpo in moto su un
piano inclinato ruvido inizialmente in
generica posizione e velocità iniziale.
Principi di
conservazione
dell’energia
meccanica
Definire
il
prodotto
scalare
tra
due
vettori
Definire il lavoro di una forza costante
per uno spostamento rettilineo in una
generica direzione rispetto alla forza.
Definire il joule.
Definire la potenza e il watt.
Definire l’energia cinetica di un corpo.
Enunciare il teorema dell’energia cinetica.
Spiegare
il
significato
di
forza
conservativa o dissipativa.
Spiegare
l’introduzione
di
un’energia
potenziale in corrispondenza di una data
forza conservativa.
Enunciare
esplicitamente
le
energie
potenziali della forza peso e della forza
elastica.
Enunciare il principio di conservazione
dell’energia meccanica.
Descrivere le varie forme di energia e le
loro continue trasformazioni nel rispetto
del bilancio.
Pagina 5 di 21
Semplici
problemi
sul
calcolo
del
lavoro, della potenza
Applicare il principio di conservazione
dell’energia meccanica alla risoluzione
di problemi con uno o due corpi
LICEO SCIENTIFICO-LINGUISTICO “A. M. DE CARLO” GIUGLIANO IN CAMPANIA(NA)
ANNO SCOLASTICO 2013/2014
Comprendere la differenza tra termoscopio e Risolvere
semplici
problemi
di
termometro.
termologia
Descrivere la dilatazione lineare, volumica Calcolare le variazioni di dimensione
dei solidi.
dei corpi sottoposti a riscaldamento
Enunciare le leggi dei gas.
Calcolare
le
quantita’
di
calore
Conoscere
le
leggi
che
regolano
le scambiate e la temperatura di equilibrio
trasformazioni dei gas perfetti.
tra due corpi a contatto
Termologia
Comprendere come avvengono i passaggi tra i
vari stati di aggregazione della materia.
Comprendere le trasformazioni reciproche di
calore e lavoro.
Riconoscere i tipi di specchi e di lenti e
le loro caratteristiche.
Ottica
Laboratorio di
Fisica
CONTENUTI
Equazioni e
disequazioni
Il piano
cartesiano
Le funzioni
La retta nel piano
cartesiano
Trasformazioni nel
piano cartesiano
La circonferenza
Risolvere semplici problemi di ottica
geometrica.
Applicare le leggi della riflessione e
della rifrazione nella formazione delle
immagini.
Misure dirette e indirette delle principali grandezze fisiche introdotte. Ricerca e/o
verifica sperimentale di alcune leggi e principi fondamentali introdotti.
OBIETTIVI SPECIFICI
SECONDO BIENNIO- NUOVO ORDINAMENTO
MATEMATICA
CLASSE TERZA -SCIENTIFICO
CONOSCENZE
ABILITA’
Ripasso:
Riconoscere e distinguere procedimenti di
equazioni e disequazioni
di secondo intersezione, unione e “discussione del segno”
grado
nella ricerca delle soluzioni di disequazioni
Sistemi di disequazioni
Saper risolvere disequazioni intere e fratte
Equazioni e disequazioni irrazionali
di
primo
e
secondo
grado,
sistemi,
Equazioni e Disequazioni con valore disequazioni irrazionali, semplici equazioni e
assoluto
disequazioni con il valore assoluto
Sistema di ascisse nel piano.
Saper associare ad una coppia di numeri reali
Distanza fra due punti.
un punto del piano.
Punto medio di un segmento.
Saper valutare la distanza fra due punti.
Baricentro e area di un triangolo.
Saper determinare il punto medio di un
segmento.
Saper determinare baricentro e area di un
triangolo.
Relazioni
Distinguere tra relazioni e funzioni.
Funzioni.
Riconoscere dominio e codominio.
Dominio, Condominio.
Interpretare funzioni e grafici nel piano
Iniettività, suriettività e
cartesiano.
biunivocità.
Saper
riconoscere
funzioni
iniettive,
Grafici.
suriettive e biunivoche.
Successioni numeriche, successioni per
Saper determinare funzioni inverse.
ricorrenza, principio di
Riconoscere le caratteristiche generali delle
induzione,progressioni aritmetiche,
successioni.
progressioni geometriche.
Determinare
il
termine
generale
di
una
successione.
Determinare
ragione
e
somma
di
una
progressione.
Successioni
definite
per
ricorrenza:
determinare il termine generale.
Applicare il principio di induzione.
Condizione di allineamento.
Stabilire l’appartenenza di un punto ad una
Equazioni implicita ed esplicita.
retta.
Rette particolari e loro equazioni.
Determinare l’equazione di una retta noti 2
Parallelismo e perpendicolarità.
punti.
Distanza punto retta.
Saper riconoscere rette particolari.
Fasci propri e impropri.
Associare
equazioni
lineare
ai
grafici
corrispondenti.
Saper ricavare l’equazione di una retta in
base alle diverse ipotesi iniziali.
Riconoscere la posizione reciproca di due
rette nel piano dall’equazione relativa.
Saper risolvere semplici problemi sulla retta
utilizzando le diverse nozioni teoriche.
Simmetrie centrali e assiali.
Conoscere le equazioni delle trasformazioni.
Traslazioni.
Saper
scrivere
le
equazioni
delle
Grafici trasformati.
trasformazioni ed applicarle alle
curve del piano.
Riconoscere le equazioni delle trasformazioni.
La circonferenza come luogo geometrico. Sapere definire l'circonferenza e farne la
Equazione
cartesiana
di
una costruzione geometrica.
circonferenza con centro in (0,0).
Saper riconoscere una circonferenza data la
Pagina 6 di 21
LICEO SCIENTIFICO-LINGUISTICO “A. M. DE CARLO” GIUGLIANO IN CAMPANIA(NA)
ANNO SCOLASTICO 2013/2014
Equazione canonica.
sua
equazione
e
disegnarla
nel
piano
Retta
e
circonferenza:
posizioni cartesiano.
reciproche.
Determinare
la
posizione
reciproca
tra
Risoluzione grafica di disequazioni circonferenza e retta e tra coniche in
irrazionali.
generale.
Determinare l'equazione della circonferenza
note particolari condizioni
Determinare l'equazione della retta tangente
ad una circonferenza.
Risolvere sistemi e disequazioni per via
grafica con l'uso della circonferenza.
La parabola come luogo geometrico
Sapere definire la parabola e farne una
Equazione
della
parabola
con
asse costruzione.
coincidente con Oy e vertice in O(0,0). Saper riconoscere una parabola data la sua
Equazione
della
parabola
con
asse equazione e disegnarla nel piano cartesiano.
parallelo ad Oy e vertice qualunque Determinare
la
posizione
reciproca
tra
ottenuta mediante traslazione.
parabola e retta e tra due parabole.
La parabola
Equazione
della
parabola
con
asse Determinare l'equazione della parabola note
parallelo ad Ox.
particolari condizioni.
Intersezione retta parabola.
Determinare l'equazione della retta tangente
Rette tangenti ad una parabola.
ad una parabola.
Risolvere sistemi e disequazioni per via
grafica con l'uso della parabola.
L’ellisse come luogo geometrico
Sapere
definire
l'ellisse
e
farne
la
Equazione
dell’ellisse
con
asse costruzione geometrica.
maggiore su Ox e su Oy.
Saper riconoscere una ellisse data la sua
Posizioni reciproche retta-ellisse
equazione e disegnarla nel piano cartesiano.
Tangenti ad una ellisse.
Determinare la posizione reciproca tra ellisse
Risoluzione grafica di disequazioni e retta e tra coniche in generale.
L’ellisse
irrazionali.
Determinare
l'equazione
dell’ellisse
note
particolari condizioni.
Determinare l'equazione della retta tangente
ad una ellisse.
Risolvere sistemi e disequazioni per via
grafica con l'uso dell’ellisse.
CONTENUTI
Grandezze fisiche
Moto rettilineo
FISICA
CLASSE TERZA -SCIENTIFICO
CONOSCENZE
Saper
enunciare
correttamente
le
definizioni di lunghezza (metro), massa
(chilogrammo) e tempo (secondo).
Distinguere
le
grandezze
fisiche,
e
relative unità di misura, di base o
fondamentali da quelle derivate.
Saper valutare gli errori sia nelle misure
dirette che in quelle indirette di una
grandezza fisica.
Sapere attribuire l’errore assoluto ad una
misura diretta sapendo la sensibilità dello
strumento usato.
Saper spiegare le cifre significative.
Saper definire le operazioni tra vettori.
Conoscere il concetto di moto rettilineo
uniforme e di velocità
Conoscere la legge del moto uniformemente
accelerato.
Conoscere la differenza tra velocità ed
accelerazione medie ed istantanee.
Conoscere le proprietà e le cause del moto
circolare
e del moto armonico e la relazione tra i
due moti.
Moto nel piano
Conoscere le equazioni del moto del
proiettile
Pagina 7 di 21
ABILITA’
Saper
calcolare,
in
casi
semplici,
l’errore assoluto o relativo di una misura
indiretta
applicando
le
leggi
di
propagazione degli errori.
Saper esprimere il risultato di una misura
con
il
corretto
uso
di
cifre
significative.
Calcolare il valore medio di una serie di
misure.
Calcolare l’errore massimo di una serie di
misure.
Saper risolvere problemi di moto
rettilineo uniforme.
Saper rappresentare la legge del moto
rettilineo uniforme nel grafico spaziotempo.
Saper
risolvere
problemi
di
moto
uniformemente accelerato
Saper rappresentare la legge del moto
rettilineo uniformemente accelerato nel
grafico spazio-tempo
Saper
applicare
le
leggi
del
moto
circolare e del moto armonico.
Saper
applicare
parabolico.
le
leggi
del
moto
LICEO SCIENTIFICO-LINGUISTICO “A. M. DE CARLO” GIUGLIANO IN CAMPANIA(NA)
ANNO SCOLASTICO 2013/2014
Conoscere le leggi di Newton.
Sapere applicare le leggi di Newton.
Essere in grado di disegnare il diagramma Saper applicare le equazioni del moto del
del corpo libero, di determinare le forze proiettile e risolvere problemi sul moto
vincolari e le forze di attrito.
dei corpi su piani inclinati.
Conoscere le proprietà e le cause del moto Saper risolvere problemi sull’equilibrio
circolare
e
del
moto
armonico
e
la dei corpi rigidi.
relazione tra i due moti.
Saper
applicare
le
leggi
del
moto
Conoscere le caratteristiche del moto del circolare e del moto armonico.
Principi della
pendolo.
dinamica
Saper descrivere moti rispetto a sistemi
inerziali differenti.
Conoscere il concetto di forza apparente.
Distinguere fra forza centripeta e forza
centrifuga.
Essere in grado di spiegare la dinamica di
semplici
moti
rispetto
a
sistemi
di
riferimento non inerziali.
Conoscere la definizione di lavoro
Saper applicare la definizione di lavoro
Conoscere e saper applicare la potenza.
alla risoluzione di problemi, in presenza
Distinguere tra forze conservative e non di forze costanti o di semplici forze
conservative.
variabili.
Conoscere l’energia cinetica e l’energia Sapere applicare la legge di conservazione
Energia meccanica
potenziale.
dell’energia cinetica alla risoluzione di
Conoscere
la
legge
di
conservazione problemi.
dell’energia cinetica.
Conoscere
la
legge
di
conservazione
dell’energia totale.
Conoscere la conservazione della quantità Saper
applicare
il
principio
di
di moto.
conservazione della quantità di moto.
Conoscere la definizione di impulso.
Sapere applicare la definizione di impulso
Conoscere i diversi tipi di urti.
e applicare alla risoluzione di problemi.
Conoscere il concetto di centro di massa.
Calcolare il momento angolare di un
Conoscere il concetto di momento di inerzia sistema fisico.
Dinamica
e momento angolare.
Applicare il principio di conservazione
rotazionale
Analizzare il moto del centro di massa di del momento angolare.
un sistema.
Risolvere semplici problemi di dinamica
Conoscere le condizioni di validità e le rotazionale.
conseguenze della conservazione del momento
angolare.
Conoscere le leggi di Keplero.
Conoscere la legge di gravitazione
universale
Gravitazione
universale
Dinamica dei
fluidi
Termologia
Conoscere le leggi che regolano la statica
dei fluidi.
Sapere il concetto di portata per una
conduttura.
Saper enunciare l’ equazione di continuità.
Saper enunciare equazione di Bernoulli.
Saper spiegare l’effetto Venturi.
Conoscere l’attrito nei fluidi , il regime
laminare, l’attrito viscoso, la legge di
Stoke, il concetto di velocità limite.
Saper
la
definizione
operativa
di
temperatura.
Conoscere le varie scale termometriche.
Dilatazione lineare e volumica dei solidi.
Dilatazione volumica dei liquidi.
Trasformazione di un gas e relative leggi.
Modello del gas perfetto e sua equazione
di stato.
Atomi, molecole, moli e legge di Avogadro.
Pressione e temperatura di un gas dal punto
di vista microscopico.
Energia interna del gas perfetto.
Energia interna nei solidi, liquidi, gas.
Calore e lavoro come forma di energia.
Capacita’ termica, calore specifico.
Trasmissione del calore per conduzione,
convezione, irraggiamento.
Il calore emesso dal Sole, l’effetto serra.
Il ruolo delle attività umane nell’aumento
dell’effetto serra.
Pagina 8 di 21
Saper applicare le leggi di Keplero.
Saper applicare la legge di gravitazione
universale.
Comprendere
il
concetto
di
campo
gravitazionale
e
saper
applicare
il
principio di conservazione dell’energia.
Analizzare il moto di pianeti e satelliti
su orbite circolari.
Calcolare la portata di una conduttura.
Comprendere la differenza tra termoscopio
e termometro.
Calcolare le variazioni di dimensione dei
corpi solidi e liquidi sottoposti a
riscaldamento.
Applicare le leggi dei gas
Calcolare la temperatura di equilibrio di
un calorimetro.
Risolvere problemi sugli scambi di calore.
LICEO SCIENTIFICO-LINGUISTICO “A. M. DE CARLO” GIUGLIANO IN CAMPANIA(NA)
ANNO SCOLASTICO 2013/2014
I passaggi tra gli stati di aggregazione.
Risolvere
problemi
sugli
stati
di
Gas e vapore.
aggregazione della materia
Laboratorio di
Fisica
CONTENUTI
Scomposizione di
un polinomio
Equazioni
Disequazioni
La circonferenza
nel piano
Il piano
cartesiano
La retta
La circonferenza
La parabola
L’ellisse
Ricerca e/o verifica sperimentale di alcune leggi e principi fondamentali introdotti.
MATEMATICA
CLASSE TERZA-LINGUISTICO
CONOSCENZE
ABILITA’
Divisioni fra polinomi. Regola di Ruffini e Calcolare
quoziente
e
resto
delle
teorema del resto.
divisione fra due polinomi.
La scomposizione in fattori
Utilizzare il teorema del resto.
Le
frazioni
algebriche,
definizioni
e Saper
individuare
le
tecniche
per
operazioni.
scomporre in fattori un polinomio e
determinare il M.C.D. e m.c.m. fra due o
più polinomi.
Saper operare con le frazioni algebriche
Equazioni di secondo grado incomplete e
Saper risolvere un’equazione di secondo
complete, le relazioni fra le radici e i
grado.
coefficienti di un’equazione di secondo Stabilire se un trinomio di secondo grado
grado,
è riducibile e, in caso affermativo,
Scomposizione di un trinomio di secondo scomporlo.
grado
Risolvere sistemi di equazioni di secondo
Equazioni di grado superiore al secondo che grado.
si
risolvono
per
scomposizione,equazioni
binomie e trinomie.
Sistemi di secondo grado.
Disequazioni di secondo grado e di grado
Saper risolvere disequazioni e sistemi di
superiore al secondo sia intere che fratte.
disequazioni.
Sistemi di disequazioni
Saper
risolvere
semplici
equazioni
e
Equazioni e disequazioni di secondo grado disequazioni con valori assoluti.
con valori assoluti
Saper
risolvere
semplici
equazioni
e
Equazioni e disequazioni irrazionali.
disequazioni irrazionali.
I luoghi geometrici. La circonferenza e il Conoscere e saper applicare i teoremi
cerchio, definizioni, le proprietà delle sulla circonferenza e sul cerchio.
corde e degli angoli al centro, angoli al
centro e angoli alla circonferenza, rette e
circonferenze .
Poligoni inscritti e circoscritti. Punti
notevoli di un triangolo. I poligoni
regolari
Sistema di ascisse nel piano.
Saper associare ad una coppia di numeri
Distanza fra due punti.
reali un punto del piano.
Punto medio di un segmento.
Saper valutare la distanza fra due punti.
Baricentro e area di un triangolo.
Saper determinare il punto medio di un
segmento.
Saper determinare baricentro e area di un
triangolo.
Condizione di allineamento.
Stabilire l’appartenenza di un punto ad
Equazioni implicita ed esplicita.
una retta.
Rette particolari e loro equazioni.
Determinare l’equazione di una retta noti
Parallelismo e perpendicolarità.
2 punti.
Distanza punto retta.
Saper riconoscere rette particolari.
Saper risolvere semplici problemi sulla
retta.
Equazione cartesiana di una circonferenza
con centro in (0,0)
Equazione canonica.
Retta
e
circonferenza:
posizioni
reciproche.
Equazione
della
parabola
con
asse
coincidente con Oy e vertice in O(0,0).
Equazione della parabola con asse parallelo
ad Oy e vertice qualunque.
Equazione della parabola con asse parallelo
ad Ox.
Intersezione retta parabola.
L’ellisse come luogo geometrico.
Equazione dell’ellisse con asse maggiore su
Ox e su Oy.
Pagina 9 di 21
Sapere definire la circonferenza e farne
la costruzione geometrica.
Saper riconoscere una circonferenza data
la sua equazione e disegnarla nel piano
cartesiano.
Determinare la posizione reciproca tra
circonferenza e retta.
Determinare
l'equazione
della
circonferenza note particolari condizioni.
Sapere definire la parabola e farne una
costruzione.
Saper riconoscere una parabola data la sua
equazione
e
disegnarla
nel
piano
cartesiano.
Sapere definire l'ellisse .
Saper riconoscere una ellisse data la sua
equazione
e
disegnarla
nel
piano
cartesiano.
LICEO SCIENTIFICO-LINGUISTICO “A. M. DE CARLO” GIUGLIANO IN CAMPANIA(NA)
L’iperbole come luogo geometrico.
L’iperbole
CONTENUTI
Strumenti
matematici
La misura
Moto rettilineo
Moti nel piano
Principi della
dinamica
Energia meccanica
Gravitazione
universale
Laboratorio di
Fisica
ANNO SCOLASTICO 2013/2014
Sapere definire l’iperbole .
Saper riconoscere una iperbole data la sua
equazione e disegnarla nel piano cartesiano.
FISICA
CLASSE TERZA-LINGUISTICO
CONOSCENZE
ABILITA’
Enunciare le equazioni tra due grandezze
Saper leggere e interpretare formule e
direttamente proporzionali o in
grafici.
relazione lineare e saperle
Saper applicare le proprietà delle potenze.
rappresentare graficamente.
Saper calcolare l’errore relativo (e
Conoscere le caratteristiche degli
percentuale) da quello assoluto e viceversa
strumenti di misura
Saper valutare gli errori sia nelle
Saper calcolare, in casi semplici, l’errore
misure dirette che in quelle indirette
assoluto o relativo di una misura indiretta
di una grandezza fisica
Sapere attribuire l’errore assoluto ad
una misura diretta sapendo la
sensibilità dello strumento usato
Saper spiegare le cifre significative
Conoscere il concetto di moto rettilineo
Saper risolvere semplici problemi di moto
uniforme e di velocità
rettilineo uniforme.
Conoscere la legge del moto
Saper rappresentare la legge del moto
uniformemente accelerato.
rettilineo uniforme nel grafico spazio-tempo.
Conoscere la differenza tra velocità ed
Saper risolvere semplici problemi di moto
accelerazione medie ed istantanee.
uniformemente accelerato
Saper rappresentare la legge del moto
rettilineo uniformemente accelerato nel
grafico spazio-tempo
Algebra dei vettori
Risolvere semplici problemi cinematici sul
Definire il vettore posizione di un
moto circolare uniforme
corpo in moto curvilineo e il vettore
spostamento tra due posizioni in due
distinti istanti
Definire il vettore velocità media di un
corpo tra due punti di una traiettoria
curvilinea.
Definire (anche non rigorosamente) il
vettore velocità istantanea di un corpo
in un punto di una traiettoria
curvilinea, indicandone la direzione
tangenziale
Saper descrivere il moto circolare
uniforme
Saper descrivere il moto armonico
Conoscere l’effetto delle forze
Conoscere le leggi di Newton
Distinguere i concetti di massa e peso
di un corpo
Definire il chilogrammo-peso e il
newton
Definire le caratteristiche della forza
d’attrito (statico e dinamico)
Distinguere fra forza centripeta e forza
centrifuga
Spiegare il concetto di forza elastica
di una molla allungata o accorciata
Usare correttamente gli strumenti e i metodi
di misura delle forze.
Calcolare il valore della forza-peso
Determinare la forza di attrito al distacco e
in movimento.
Utilizzare la legge di Hooke per il calcolo
delle forze elastiche
Conoscere la definizione di lavoro
Conoscere e saper applicare la
definizione di potenza.
Distinguere tra forze conservative e non
conservative.
Conoscere l’energia cinetica e l’energia
potenziale.
Conoscere la legge di conservazione
dell’energia cinetica
Conoscere la legge di conservazione
dell’energia totale.
Saper applicare la definizione di lavoro alla
risoluzione di semplici problemi.
Conoscere le leggi di Keplero.
Conoscere la legge di gravitazione
universale.
Saper applicare le leggi di Keplero.
Saper applicare la legge di gravitazione
universale .
Ricerca e/o verifica sperimentale di alcune leggi e principi fondamentali introdotti
Pagina 10 di 21
LICEO SCIENTIFICO-LINGUISTICO “A. M. DE CARLO” GIUGLIANO IN CAMPANIA(NA)
CONTENUTI
L’iperbole
Statistica
Funzioni
goniometriche
Trigonometria
Funzioni
esponenziali e
logaritmiche
Approfondimenti
CONTENUTI
Termologia
Termodinamica
ANNO SCOLASTICO 2013/2014
MATEMATICA
CLASSE QUARTA - SCIENTIFICO
CONOSCENZE
ABILITA’
L’iperbole come luogo geometrico.
Sapere definire l’iperbole con riga e compasso
Proprietà e simmetrie.
e farne una costruzione.
Iperbole equilatera.
Saper riconoscere una iperbole data la sua
Iperbole equilatera riferita ai suoi
equazione e disegnarla nel piano cartesiano.
asintoti.
Determinare la posizione reciproca tra
Funzione omografica.
iperbole e retta e tra due iperbole.
Determinare l'equazione della iperbole note
particolari condizioni.
Determinare l'equazione della retta tangente
ad una iperbole.
Nozioni
di
base
della
statistica Risolvere semplici problemi di statistica
descrittiva.
Funzioni
goniometriche
e
grafici Saper definire le funzioni goniometriche
relativi.
fondamentali e saper tracciare il loro
Formule goniometriche.
grafico.
Equazioni e disequazioni elementari, Saper ricavare le funzioni goniometriche di
lineari,
omogenee
o
ad
esse angoli particolari.
riconducibili.
Saper utilizzare le principali formule di
goniometria.
Saper riconoscere identità goniometriche.
Saper
risolvere
equazioni
e
disequazioni
goniometriche con i metodi opportuni.
I teoremi sui triangoli rettangoli.
Saper risolvere i triangoli e utilizzare i
Relazioni tra lati e angoli di un teoremi di trigonometria per la risoluzione di
triangolo rettangolo.
problemi geometrici.
Teoremi sui triangoli qualunque.
La funzione esponenziale.
Saper
risolvere
equazioni
e
disequazioni
La funzione logaritmica come inversa esponenziali.
della funzione esponenziale.
Saper risolvere
equazioni e disequazioni
Saper
dimostrare
le
proprietà
dei logaritmiche
logaritmi.
Saper risolvere
equazioni e disequazioni
esponenziali utilizzando la definizione di
logaritmo.
Problemi classici dell’antichità
Comprendere il significato di trisecare un
angolo, quadrare il cerchio,duplicare il cubo.
FISICA
CLASSE QUARTA - SCIENTIFICO
CONOSCENZE
ABILITA’
Saper
la
definizione
operativa
di Comprendere la differenza tra termoscopio e
temperatura
termometro
Conoscere le varie scale termometriche
Calcolare le variazioni di dimensione dei
Dilatazione lineare e volumica dei corpi
solidi
e
liquidi
sottoposti
a
solidi
riscaldamento
Dilatazione volumica dei liquidi
Trasformazione di un gas e relative Risolvere semplici problemi di termologia
leggi
Modello
del
gas
perfetto
e
sua
equazione di stato
Atomi, molecole, moli e legge di
Avogadro.
Pressione e temperatura di un gas dal
punto di vista microscopico
Energia interna del gas perfetto
Energia interna nei solidi, liquidi,
gas
Calore e lavoro come forma di energia
Calcolare la temperatura di equilibrio di un
Capacita’ termica, calore specifico
calorimetro
Trasmissione del calore per conduzione, Calcolare le quantità di calore scambiate e la
convezione, irraggiamento
temperatura di equilibrio tra due corpi a
Il calore emesso dal Sole, l’effetto contatto
serra
Il
ruolo
delle
attività
umane
nell’aumento dell’effetto serra
I
passaggi
tra
gli
stati
di Risolvere problemi sugli stati di aggregazione
aggregazione
della materia
Gas e vapore
Riconoscere il lavoro e il calore come Saper applicare il primo principio all’analisi
energia in transito
delle trasformazioni termodinamiche
Distinguere
fra
trasformazioni
reversibili e irreversibili
Pagina 11 di 21
LICEO SCIENTIFICO-LINGUISTICO “A. M. DE CARLO” GIUGLIANO IN CAMPANIA(NA)
ANNO SCOLASTICO 2013/2014
Rappresentare graficamente il lavoro
termodinamico
Conoscere le proprietà termodinamiche
delle diverse trasformazioni
Conoscer le proprietà delle macchine
termiche
e
saperne
calcolare
il
rendimento
Comprendere il significato del secondo
principio e di entropia
Saper definire l’elettrizzazione di un
Saper calcolare la Legge di Coulomb per le
corpo e conoscere i vari tipi di
cariche puntiformi
elettrizzazione
Saper commentare ed applicare il concetto di
Saper enunciare la Legge di Coulomb per campo elettrico E
le cariche puntiformi
Saper disegnare le linee di forza per campi
Saper definire il concetto di campo e
elementari
di campo elettrico E
Utilizzare il Teorema di Gauss per determinare
Il flusso del campo elettrico
il campo elettrico in alcune situazioni
Saper enunciare e dimostrare il
Determinare il vettore campo elettrico
teorema di Gauss e conoscere le sue
risultante da una distribuzione di cariche
applicazioni
Saper calcolare il potenziale elettrico e la
Saper definire il potenziale elettrico
differenza di potenziale
e la differenza di potenziale
Utilizzare la relazione tra campo elettrico e
Superfici equipotenziali
potenziale
Circuitazione del campo elettrostatico
Comprendere il significato di campo
Elettrostatica
conservativo e il suo legame con la
circuitazione
Il campo elettrico e il potenziale
all'interno e all'esterno di conduttori
in equilibrio elettrostatico
La capacità di un conduttore
Distinguere i collegamenti di conduttori in
Il condensatore, i condensatori in
serie e in parallelo
serie e in parallelo
Calcolare
la capacità di conduttori e
L'energia immagazzinata in un
condensatori
condensatore
Analizzare circuiti contenenti condensatori in
L'esperienza di Millikan
serie e in parallelo
Calcolare
l’energia
immagazzinata
in
un
condensatore
Descrivere il processo di carica e scarica di
un condensatore
Saper definire la corrente elettrica.
Utilizzare in maniere corretta i simboli per i
Conoscere ed applicare le leggi di Ohm. circuiti elettrici.
Conoscere ed applicare i Principi di
Comprendere il ruolo della resistenza interna
Kirchoff.
di un generatore.
Conoscere gli effetti chimici e termici Descrivere l’effetto Volta e l’effetto
di una corrente: la trasformazione
termoionico.
dell’energia
Descrivere la conduzione nei liquidi e nei
elettrica, l’effetto Joule.
gas.
Elettrodinamica
La forza elettromotrice e la resistenza Saper descrivere i fenomeni che evidenziano
interna di un generatore di tensione.
la natura di interazioni magnetiche dovute sia
La seconda legge di Ohm e la
ai singoli magneti che alle correnti
resistività di un conduttore.
L’effetto Volta, La Pila di Volta.
La corrente elettrica nei liquidi e nei
gas.
Saper definire il campo magnetico.
Laboratorio di
Ricerca e/o verifica sperimentale di alcune leggi e principi fondamentali introdotti
Fisica
Pagina 12 di 21
LICEO SCIENTIFICO-LINGUISTICO “A. M. DE CARLO” GIUGLIANO IN CAMPANIA(NA)
ANNO SCOLASTICO 2013/2014
OBIETTIVI SPECIFICI
SCIENTIFICO VECCHIO ORDINAMENTO
MATEMATICA - PNI
CLASSE QUINTA
CONTENUTI
CONOSCENZE
ABILITA’
Saper enunciare e dimostrare il teorema Calcolare limiti di semplici funzioni.
della permanenza del segno.
Applicare la continuità e le proprietà
Saper enunciare e dimostrare il teorema dell’algebra dei limiti per risolvere limiti
del confronto.
e forme di indecisione.
Definizione di funzione continua in un
Conoscere e applicare i limiti notevoli.
Teoremi sui limiti punto e un intervallo.
Classificare la specie di punti discontinuità.
Conoscere i teoremi sulle funzioni
continue.
Punti di discontinuità.
Forme indeterminate.
Conoscere i limiti fondamentali.
Il rapporto incrementale.
Saper calcolare l’equazione della tangente e
Derivata di una funzione in un punto e
della normale al grafico di una funzione f in
suo significato geometrico.
un punto.
Continuità delle funzioni derivabili.
Stabilire relazioni fra il grafico di y’ ed il
Interpretazione geometrica di alcuni
grafico di y.
casi di non derivabilità (flesso a
Interpretare geometricamente alcuni casi di
tangente verticale,cuspide, punto
non derivabilità.
angoloso).
Calcolare
derivate
di
semplici
funzioni
Derivate delle principali funzioni.
applicando i teoremi studiati.
Regole di derivazione.
Calcolare le derivate
successive di
una
Derivazione di funzioni composte.
funzione data.
Derivazione di funzioni inverse.
Calcolare il differenziale e interpretare
Derivate di ordine superiore.
geometricamente
il
differenziale
di
una
I teoremi fondamentali sulle funzioni
funzione.
derivabili :Teorema di Rolle . Teorema
Saper determinare gli intervalli in cui una
di Lagrange e sue conseguenze . Teorema funzione è crescente [decrescente].
Calcolo
di Cauchy. Teoremi di De L’Hospital.
Saper determinare massimi e minimi assoluti e
differenziale
Definizione di differenziale e
relativi mediante il segno della derivata
applicazioni.
prima.
Funzioni monotone.
Saper dimostrare il teorema per le funzioni
Massimi e minimi.
derivabili.
Riconoscere gli estremi di una funzione non
derivabile in un punto.
Saper individuare i punti di massimi e minimi
assoluti.
Saper risolvere problemi di massimo e minimo.
Determinare concavità, convessità e flessi, e
conoscere i teoremi relativi.
Determinare gli asintoti di una funzione.
Costruire un grafico coerente per una funzione
reale di una variabile reale, in base ad una
equazione assegnata.
Interpretare l’andamento di una funzione in
base ad informazioni desunte dal suo grafico.
Primitive di funzioni elementari.
Calcolare primitive di funzioni elementari.
Principali formule di integrazione.
Saper utilizzare la tecnica più opportuna per
Integrazione per scomposizione di
trovare la primitiva di una funzione.
funzioni elementari.
Calcolare
primitive
di
alcune
semplici
Principali formule di integrazione.
funzioni razionali fratte con denominatore a
Introduzione al concetto di
radici semplici reali e radici complesse.
integrale definito
Saper applicare il teorema della media.
Somme inferiori, somme superiori
Determinare il valore medio di una funzione.
Definire l’integrale definito di una
Calcolare semplici aree di domini piani.
funzione continua su un intervallo
Calcolare
volumi
di
semplici
solidi
di
chiuso.
rotazione.
Calcolo integrale
Conoscere le proprietà degli integrali
Calcolare aree di domini piani utilizzando
definiti.
integrali generalizzati.
Saper enunciare e dimostrare il teorema Calcolare la lunghezza di un arco di curva.
della media.
Funzione integrale.
Saper dimostrare il teorema di
Torricelli.
Calcolo di aree.
Calcolo dei volumi dei solidi di
rotazione.
Integrali generalizzati.
Lunghezza di un arco di curva.
Integrale
Conoscere il significato di
Calcolare semplici integrali impropri dei due
improprio
integrazione in senso improprio
tipi
Equazioni
Equazioni differenziali del primo
Saper risolvere semplici equazioni
differenziali
ordine, del secondo
differenziali del primo ordine, del secondo.
Risoluzione
Risoluzione approssimata di equazioni
Ricercare approssimazioni per gli zeri di una
approssimata
(Metodo di bisezione. Metodo delle
funzione.
di equazioni
tangenti. Metodo delle secanti).
Valutare le approssimazioni.
Pagina 13 di 21
LICEO SCIENTIFICO-LINGUISTICO “A. M. DE CARLO” GIUGLIANO IN CAMPANIA(NA)
ANNO SCOLASTICO 2013/2014
Calcolo approssimato di aree piane
Calcolare
approssimazioni
di
aree
piane
Calcolo approssimato di superfici di
delimitate da archi di curva
solidi
Calcolare
approssimazioni
della
superficie
Calcolo approssimato di volumi di
generata per rotazione e/o traslazione di un
Integrazione
solidi di rotazione
arco di curva.
numerica
(Metodo dei rettangoli.
Calcolare approssimazioni del volume di un
Metodo dei trapezi. Metodo di
solido generato da un’area per rotazione
Cavalieri Simpson).
attorno ad un asse e/o traslazione di un’area
chiusa e limitata
Conoscere le disposizioni semplici e Saper risolvere semplici problemi sul calcolo
con ripetizione.
combinatorio.
Conoscere
le permutazioni semplici e Saper risolvere semplici problemi sul calcolo
con ripetizione.
delle probabilità.
Conoscere la funzione n!
Calcolo
Conoscere le combinazioni semplici e
combinatorio
con ripetizione.
e calcolo delle
Conoscere i coefficienti binomiali
probabilità
Conoscere il concetto di evento
Conoscere
le diverse definizioni di
probabilità.
Conoscere
la
somma
logica
ed
il
prodotto logico di eventi.
Geometrie non euclidee: Il quinto
Descrivere la struttura della geometria
postulato di Euclide, il metodo
euclidea
assiomatico e le geometrie non euclidee Analizzare il V postulato di Euclide
Inquadrare l’iter storico e logico che ha
portato a costruire le geometrie non euclidee
Presentare le caratteristiche di base della
Approfondimenti
geometria iperbolica ed ellittica
Riflettere sui contenuti della matematica e
dei suoi metodi
Considerare la matematica nel
contesto del pensiero scientifico e
filosofico .
CONTENUTI
Teoria dei Limiti
Teoremi sui limiti
Calcolo
differenziale
MATEMATICA – TRADIZIONALE
CLASSE QUINTA
CONOSCENZE
ABILITA’
Conoscere la definizione di intorno di
Saper fare la verifica di un limite finito o
un punto, intorno circolare, punto di
infinito di una funzione per x che tende a x0
accumulazione
, a ±∞
Conoscere la definizione di limite
Saper eseguire le operazioni sui limiti
Conoscere la definizione di funzione
riconoscendo le forme indeterminate
continua in un punto e in un intervallo
Saper enunciare e dimostrare il teorema Applicare la continuità e le proprietà
della permanenza del segno
dell’algebra dei limiti per risolvere limiti
Saper enunciare e dimostrare il teorema e forme di indecisione
del confronto
Conoscere e applicare i limiti notevoli
Definizione di funzione continua in un
Classificare la specie di punti discontinuità
punto e un intervallo
Conoscere i teoremi sulle funzioni
continue
Punti di discontinuità
Forme indeterminate
Conoscere i limiti fondamentali
Il rapporto incrementale
Saper calcolare l’equazione della tangente e
Derivata di una funzione in un punto e
della normale al grafico di una funzione f in
suo significato geometrico
un punto.
Continuità delle funzioni derivabili
Stabilire relazioni fra il grafico di y’ ed il
Interpretazione geometrica di alcuni
grafico di y.
casi di non derivabilità
Interpretare geometricamente alcuni casi di
Derivate delle principali funzioni
non derivabilità
Regole di derivazione
Calcolare derivate di semplici funzioni
Derivazione di funzioni composte,
applicando i teoremi studiati
derivazione di funzioni inverse
Calcolare le derivate successive di una
Derivate di ordine superiore
funzione data
I teoremi fondamentali sulle funzioni
Calcolare il differenziale e interpretare
derivabili :Teorema di Rolle . Teorema
geometricamente il differenziale di una
di Lagrange e sue conseguenze . Teorema funzione
di
Saper determinare gli intervalli in cui una
Cauchy. Teoremi di De L’Hospital.
funzione è crescente [decrescente].
Definizione di differenziale e
Saper determinare massimi e minimi assoluti e
applicazioni
relativi. mediante il segno della derivata
Funzioni monotone
prima
Massimi e minimi
Saper dimostrare il teorema per le funzioni
derivabili
Riconoscere gli estremi di una funzione non
derivabile in un punto
Saper individuare i punti di massimi e minimi
assoluti
Saper risolvere problemi di massimo e minimo
Pagina 14 di 21
LICEO SCIENTIFICO-LINGUISTICO “A. M. DE CARLO” GIUGLIANO IN CAMPANIA(NA)
ANNO SCOLASTICO 2013/2014
Determinare concavità, convessità e flessi. E
conoscere i teoremi relativi.
Determinare gli asintoti di una funzione
Costruire un grafico coerente per una funzione
reale di una variabile reale, in base ad una
equazione assegnata.
Interpretare l’andamento di una funzione in
base ad informazioni desunte dal suo grafico
Primitive di funzioni elementari
Calcolare primitive di funzioni elementari
Principali formule di integrazione
Conoscere
le
principali
formule
di
Integrazione per scomposizione di
integrazione
funzioni
Calcolare primitive mediante integrazione per
elementari
scomposizione
Principali formule di integrazione
integrazione per parti
Integrazione per scomposizione
integrazione per sostituzione
Integrazione per parti
Calcolare
primitive
di
alcune
semplici
integrazione per sostituzione
funzioni razionali fratte con denominatore a
Integrazione delle funzioni razionali
radici reali semplici e radici complesse
fratte con denominatore a radici reali
Riconoscere situazioni in cui è necessario
semplici e radici
ricorrere al concetto di integrale
complesse
Definire l’integrale di una funzione continua
Calcolo integrale
Problema delle aree
su un intervallo chiuso
Conoscere
le
proprietà
degli
integrali
definiti
Conoscere e applicare il teorema della media
Determinare il valore medio di una funzione
Definire una funzione integrale
Dimostrare il teorema di Torricelli.
Significato geometricio
Calcolare semplici aree di domini piani
Calcolare
volumi
di
semplici
solidi
di
rotazione
Calcolare aree di domini piani utilizzando
integrali
generalizzati
Geometrie non euclidee: Il quinto
Descrivere la struttura della geometria
postulato di Euclide, il metodo
euclidea
assiomatico e le geometrie non euclidee Analizzare il V postulato di Euclide
Inquadrare l’iter storico e logico che ha
portato a costruire le geometrie non euclidee
Approfondimenti
Presentare le caratteristiche di base della
geometria iperbolica ed ellittica
Riflettere sui contenuti della matematica e
dei suoi metodi
Considerare la matematica nel contesto del
pensiero scientifico e filosofico .
CONTENUTI
Elettrostatica
FISICA
CLASSE QUINTA - SCIENTIFICO
CONOSCENZE
ABILITA’
Saper definire l’elettrizzazione di un Saper calcolare la Legge di Coulomb per le
corpo e conoscere i vari tipi di cariche puntiformi.
elettrizzazione.
Saper commentare ed applicare il concetto di
Saper enunciare la Legge di Coulomb per
le cariche puntiformi.
campo elettrico E
Saper definire il concetto di campo e Saper disegnare le linee di forza per campi
elementari.
Utilizzare il Teorema di Gauss per determinare
di campo elettrico E
Il flusso del campo elettrico
il campo elettrico in alcune situazioni.
Saper
enunciare
e
dimostrare
il Determinare il vettore campo elettrico
teorema di Gauss e conoscere le sue risultante da una distribuzione di cariche.
applicazioni.
Saper calcolare il potenziale elettrico e la
Saper definire il potenziale elettrico differenza di potenziale.
e la differenza di potenziale.
Utilizzare la relazione tra campo elettrico e
Superfici equipotenziali.
potenziale.
Circuitazione del campo elettrostatico. Comprendere il significato di campo
conservativo e il suo legame con la
circuitazione.
Il campo elettrico e il potenziale
all'interno e all'esterno di conduttori
in
equilibrio elettrostatico.
La capacità di un conduttore.
Distinguere i collegamenti di conduttori in
Il condensatore, i condensatori in
serie e in parallelo.
serie e in parallelo.
Calcolare la capacità di conduttori e
L'energia immagazzinata in un
condensatori.
Pagina 15 di 21
LICEO SCIENTIFICO-LINGUISTICO “A. M. DE CARLO” GIUGLIANO IN CAMPANIA(NA)
ANNO SCOLASTICO 2013/2014
Condensatore.
Analizzare circuiti contenenti condensatori in
L'esperienza di Millikan.
serie e in parallelo.
Calcolare l’energia immagazzinata in un
condensatore in un condensatore.
Descrivere il processo di carica e scarica di
un condensatore.
Le correnti
elettriche
La
magnetostatica
Il campo
elettromagnetico
Laboratorio di
Fisica
Saper definire la corrente elettrica.
Conoscere ed applicare le leggi di Ohm.
Conoscere ed applicare i Principi di
Kirchoff.
Conoscere gli effetti chimici e termici
di una corrente: la trasformazione
dell’energia
elettrica, l’effetto Joule.
La forza elettromotrice e la resistenza
interna di un generatore di tensione.
La seconda legge di Ohm e la
resistività di un conduttore.
L’effetto Volta, La Pila di Volta.
La corrente elettrica nei liquidi e nei
gas.
Utilizzare in maniere corretta i simboli per i
circuiti elettrici.
Comprendere il ruolo della resistenza interna
di un generatore.
Descrivere l’effetto Volta e l’effetto
termoionico.
Descrivere la conduzione nei i liquidi e nei
gas.
Saper definire il campo magnetico.
Saper definire il vettore forza di un
campo magnetico.
Conoscere il fenomeno di induzione
magnetica.
Conoscere le leggi dell’induzione
magnetica.
Il campo magnetico generato da un filo
percorso da corrente, da una spira, da
un solenoide.
La forza di Lorentz e il moto di una
carica in un campo magnetico uniforme.
Il flusso e la circuitazione del campo
magnetico.
Il Teorema di Gauss e Teorema di Ampere
per il campo magnetico.
Le proprietà magnetiche della materia e
il ciclo di isteresi magnetica.
L’elettromagnete.
Rappresentare l’andamento di un campo
magnetico disegnandone le linee di forza.
Determinare l’intensità della forza che si
manifesta tra fili percorsi da corrente e su
un filo percorso da
Corrente.
Determinare intensità, direzione, verso del
campo magnetico generato da fili rettilinei,
spire, solenoidi percorsi da corrente.
Comprendere il principio di funzionamento del
motore elettrico.
Determinare intensità, direzione, verso della
forza agente su una carica in moto.
Analizzare il moto di una particella carica in
un campo magnetico uniforme.
Comprendere il significato del Teorema di
Gauss e del Teorema di Ampere per il campo
magnetico
Descrivere le proprietà magnetiche della
materia
Spiegare in che modo si produce una corrente
indotta
Ricavare la legge di Faraday – Neumann
Interpretare la legge di Lenz
Le correnti indotte e il ruolo del
flusso del campo magnetico
La legge di Faraday – Neumann –
Lenz
Ricerca e/o verifica sperimentale di alcune leggi e principi fondamentali introdotti
Pagina 16 di 21
LICEO SCIENTIFICO-LINGUISTICO “A. M. DE CARLO” GIUGLIANO IN CAMPANIA(NA)
ANNO SCOLASTICO 2013/2014
CONTENUTI
PRIMO
QUADRIMESTRE
SECONDO
QUADRIMESTRE
PRIMO
QUADRIMESTRE
SECONDO
QUADRIMESTRE
PRIMO
QUADRIMESTRE
SECONDO
QUADRIMESTRE
PRIMO
QUADRIMESTRE
SECONDO
QUADRIMESTRE
PRIMO
QUADRIMESTRE
SECONDO
QUADRIMESTRE
PRIMO
QUADRIMESTRE
SECONDO
QUADRIMESTRE
PRIMO
QUADRIMESTRE
SECONDO
QUADRIMESTRE
PRIMO
QUADRIMESTRE
SECONDO
QUADRIMESTRE
PRIMO
QUADRIMESTRE
SECONDO
QUADRIMESTRE
PRIMO
QUADRIMESTRE
SECONDO
QUADRIMESTRE
PRIMO
QUADRIMESTRE
SECONDO
QUADRIMESTRE
PRIMA CLASSE-FISICA
Strumenti matematici. La misura.
Le grandezze.
L’equilibrio dei solidi.
Le forze.
L’equilibrio dei liquidi
SECONDA CLASSE -FISICA
Moto rettilineo. Moto rettilineo uniformemente accelerato
circolare Principi della dinamica
Termologia. Ottica
Le funzioni.
Moto curvilineo.
Moto
TERZA CLASSE- MATEMATICA SCIENTIFICO
La retta
Le trasformazioni nel piano.
La circonferenza.
La parabola.
L’ellisse.
TERZA CLASSE – FISICA SCIENTIFICO
Le grandezze fisiche. Moti rettilinei. Moti nel piano. Principi della dinamica
Energia meccanica Dinamica dei fluidi
Dinamica rotazionale.
Gravitazione universale, termologia.
TERZA CLASSE- MATEMATICA LINGUISTICO
Scomposizione di un polinomio. Equazioni e disequazioni. Il piano cartesiano.
La retta nel piano
La circonferenza nel piano. La circonferenza. La parabola. l’ellisse.
L’iperbole.
TERZA CLASSE- FISICA LINGUISTICO
Le grandezze fisiche, moti rettilinei
Moti nel piano, principi della dinamica, energia meccanica
QUARTA CLASSE- MATEMATICA
Iperbole, statistica, funzioni goniometriche, equazioni e disequazioni
goniometriche
Trigonometria, funzioni esponenziali e logaritmiche, equazioni e disequazioni
esponenziali e logaritmiche
QUARTA CLASSE- FISICA
Termologia e termodinamica
Elettrostatica-Elettrodinamica
QUINTA CLASSE- MATEMATICA PNI
Teoremi sui limiti. Calcolo differenziale. Studio del grafico di una funzione.
Problemi di massimo e di minimo
Calcolo integrale. Integrale improprio. Equazioni differenziali. Risoluzione
approssimata di equazioni. Integrazione numerica. Calcolo combinatorio e calcolo
delle probabilità
QUINTA CLASSE – MATEMATICA TRADIZIONALE
Teoria dei limiti. Teoremi sui limiti. Grafico probabile.
Calcolo differenziale.
Elettrostatica.
La
Calcolo integrale.
QUINTA CLASSE - FISICA
Elettrodinamica.
magnetostatica.
Il campo elettromagnetico.
Pagina 17 di 21
LICEO SCIENTIFICO-LINGUISTICO “A. M. DE CARLO” GIUGLIANO IN CAMPANIA(NA)
ANNO SCOLASTICO 2013/2014
METODOLOGIE
Poiché l’efficacia dell’intervento educativo-didattico dipende prevalentemente dalla motivazione
e dal grado di coinvolgimento dello studente, saranno adottate le strategie più efficaci per
stimolare la curiosità, la creatività e l'operatività degli allievi sollecitandoli ad assumere
un atteggiamento critico e attivo nel proprio processo di apprendimento.
Per quanto possibile, gli argomenti saranno introdotti in forma di situazioni problematiche e
gli studenti saranno sollecitati a riconoscere relazioni e a formulare ipotesi di soluzione
facendo ricorso a conoscenze già acquisite e anche all'intuito e alla fantasia.
Attraverso procedimenti di tipo deduttivo, saranno guidati alla generalizzazione del risultato
conseguito e alla sintesi con altre nozioni teoriche già apprese.
Saranno favorite le attività pratiche e l’approccio sperimentale attraverso la frequentazione
dei laboratori scientifici e informatici.
In sintesi, saranno valorizzati tutti gli aspetti del lavoro scolastico:
approccio per problemi alle principali questioni affrontate
pratica del metodo induttivo-deduttivo sia nell’interpretazione dei fenomeni naturali che
nella risoluzione di problemi, nella dimostrazione di teoremi e nella costruzione di
modelli e di teorie
presentazione rigorosa degli argomenti e immediata applicazione degli stessi
rielaborazione individuale dei contenuti anche attraverso l’esercizio di lettura, di
analisi, e d’interpretazione del testo scientifico
pratica dell’argomentazione e del confronto
cura di una modalità espositiva scritta ed orale corretta, pertinente, efficace e
personale
uso dei laboratori scientifici e informatici
uso degli strumenti multimediali a supporto dello studio e della ricerca.
Le metodologie didattiche, utilizzate dai docenti
programmati, si concretizzeranno in termini di:
per
il
raggiungimento
degli
obiettivi
Situazioni di apprendimento
Lezione frontale, lezione interattiva/dialogica, lavori di gruppo e individuali, ricerche
guidate, relazioni, esercitazioni di autocorrezione, problem-solving, simulazioni, approcci
didattici individualizzati e di recupero per una più efficace partecipazione operativa degli
alunni.
Materiali di supporto allo sviluppo dei contenuti
Testi in adozione e/o consigliati, libri della biblioteca, riviste e quotidiani, presentazioni
multimediali, documenti originali, tavole e grafici, documenti reperibili in rete, software di
base e applicativi.
Strumenti di lavoro
Quaderni, schede, fotocopie, lavagna tradizionale, lavagna interattiva
computer, CD-ROM, strumentazione dei laboratori scientifici e informatici
multimediale
LIM,
VERIFICHE
Le verifiche, sistematiche e periodiche, saranno articolate in riferimento agli
generali e agli obiettivi specifici prefissati per ogni singolo segmento.
Si avrà cura di somministrare prove a vari livelli di complessità per consentire ad
dare risposte adeguate alle proprie capacità, tenendo conto non solo delle esigenze
particolari difficoltà, ma anche di quelle di chi dimostra maggiori abilità e
interesse.
obiettivi
ognuno di
di chi ha
più vivo
Le verifiche scritte /test su argomenti circoscritti che possono costituire anche valutazioni
per l’orale e risultano utili strumenti di valutazione formativa permettendo, ove necessario, di
riprendere eventuali argomenti poco assimilati.
Avranno, per lo più, la durata di una ora, saranno corrette e discusse con gli alunni.
Pagina 18 di 21
LICEO SCIENTIFICO-LINGUISTICO “A. M. DE CARLO” GIUGLIANO IN CAMPANIA(NA)
ANNO SCOLASTICO 2013/2014
Le prove scritte di contenuto più ampio che, di norma costituiscono valutazioni per lo scritto,
saranno utilizzate come strumenti di verifica finale.
Per la Fisica avranno durata di una ora, mentre per Matematica avranno , di norma, la durata di
due ore. Al fine di preparare gli allievi ad affrontare la seconda e la terza prova scritta
previste dal nuovo Esame di Stato le prove scritte saranno articolate nelle forme più varie,
dalle tipologie più tradizionali (esercizi, problemi, trattazioni sintetiche) ai test e alle
prove strutturate.
Le interrogazioni orali mireranno soprattutto a valutare le capacità di ragionamento, di
rielaborazione personale e di comunicazione attraverso un linguaggio proprio, chiaro e corretto;
per controllare il lavoro a casa, per verificare
l’applicazione del singolo alunno e infine
come rinforzo per tutta la classe.
Le verifiche scritte e orali saranno frequenti e omogeneamente distribuite nell’arco dell’anno.
Nel primo periodo della attività scolastica (Settembre – Gennaio) sono previste almeno due prove
scritte mentre nel secondo periodo ( Gennaio – Giugno ) almeno tre prove scritte.
VALUTAZIONE
Criteri
La valutazione formativa e sommativa mirerà all’accertamento delle conoscenze e delle abilità
acquisite dall’allievo; inoltre si terrà conto del livello di partenza, della partecipazione,
dell'impegno, del grado di socializzazione e di maturazione.
La valutazione, fornendo all'insegnante le informazioni necessarie circa le condizioni di
apprendimento del singolo allievo, costituirà la base diagnostica per un perfezionamento ed una
maggiore individualizzazione dell'intervento formativo e guiderà gradualmente il ragazzo alla
scoperta delle sue reali possibilità e alla loro massima utilizzazione.
Per la formulazione del giudizi e l’attribuzione dei voti, relativamente alle verifiche
formative e sommative, ciascun docente considererà i seguenti elementi
Orale
Conoscenza dell’argomento/procedimento richiesto.
Realizzazione di collegamenti, sviluppi, confronti, applicazioni.
Argomentazione e rielaborazione personale critica
Apporti originali e creativi.
Lessico ed esposizione.
Scritto
Conoscenza e sviluppo dell’argomento richiesto.
Applicazione del procedimento richiesto.
Organizzazione e articolazione del testo e/o dei dati.
Organicità del progetto applicativo, e/o risolutivo.
Approfondimenti e generalizzazioni, giudizi e interpretazioni personali
Lessico ed esposizione.
Indicatori
Il docente assumerà i seguenti indicatori del livello di sufficienza
Orale
L’alunno deve conoscere in modo abbastanza corretto gli argomenti/procedimenti richiesti e saper
esprimere,se invitato, giudizi accettabili su di essi. Deve esporre senza particolari
difficoltà.
Scritto
La prova tratta/sviluppa/risolve l’argomento/quesito/problema richiesto nelle linee essenziali
in modo abbastanza chiaro e lineare. Lo svolgimento è nel complesso corretto, senza gravi o
frequenti errori.
La valutazione finale terrà conto della partecipazione al dialogo educativo, dell’ impegno
profuso, del metodo di studio utilizzato, delle competenze acquisite; viene pertanto utilizzata
Pagina 19 di 21
LICEO SCIENTIFICO-LINGUISTICO “A. M. DE CARLO” GIUGLIANO IN CAMPANIA(NA)
ANNO SCOLASTICO 2013/2014
la seguente griglia:
VOTO
IMPEGNO
METODO DI LAVORO
COMPETENZE
10
Il suo impegno è
stato continuo ed
efficace
Ha acquisito un metodo di
lavoro rigoroso
Ha conseguito un completo possesso dei
contenuti disciplinari e sicure abilità
operative
9
Il suo impegno è
stato produttivo
Ha acquisito un proficuo
metodo di lavoro
Si è distinto per il livello di
conoscenze disciplinari ed abilità
operative raggiunto
8
Il suo impegno è
stato regolare
Ha acquisito autonomia nel Ha conseguito un livello di conoscenze
metodo di lavoro
disciplinari ed abilità operative più che
buono
7
Il suo impegno non E’ in possesso di un metodo Ha conseguito un buon livello di
è stato sempre
di lavoro organizzato, ma
conoscenze disciplinari e di abilità
regolare
non sempre proficuo
operative
6
Il suo impegno è
stato inefficace
Il suo metodo di lavoro non Ha conseguito una sostanziale conoscenza
è ben organizzato
dei contenuti disciplinari
5
Il suo impegno è
stato limitato
Il suo metodo di lavoro è
poco organizzato
<=4
Ha conseguito una conoscenza lacunosa
e
frammentaria dei contenuti disciplinari
E’ in possesso di un metodo Manifesta scarsissima conoscenza dei
di lavoro disordinato e
contenuti e pochissime o nessuna abilità.
dispersivo
Mentre per il comportamento la seguente griglia:
VOTO DECIMALE
COMPORTAMENTO
DESCRITTORI
L’alunno instaura ottimi rapporti relazionali; è solidale e
Relazionalità
collaborativo.
Maturità affettiva
Possiede un completo autocontrollo.
Partecipa alle attività didattico - educative in modo attivo
Partecipazione
e costruttivo.
Impegno
Si impegna in modo produttivo ed efficace.
Metodo di lavoro
Opera in modo corretto anche in situazioni complesse; sceglie
percorsi risolutivi alternativi.
10
Condotta
Relazionalità
9
Maturità affettiva
Partecipazione
Impegno
Metodo di lavoro
Condotta
Relazionalità
Maturità affettiva
L’alunno mostra un comportamento esemplare; è sempre
rispettoso delle regole condivise e rispettoso nei confronti
delle persone e delle cose. Svolge il proprio dovere con
responsabilità. Si pone come elemento trainante positivo
all’interno della classe.
L’alunno instaura validi rapporti di relazione; rispetta le
iniziative altrui.
Possiede una piena capacità di autocontrollo.
Partecipa alle attività didattico-educative in modo
sistematico.
Si impegna in modo continuo e costante.
Opera autonomamente in modo corretto anche in situazioni
complesse.
L’alunno mostra un comportamento esemplare; è sempre
rispettoso delle regole condivise e rispettoso nei confronti
delle persone e delle cose. Svolge il proprio dovere con
responsabilità.
L’alunno evidenzia positive capacità di relazione; accetta il
confronto con gli altri.
Possiede una valida capacità di autocontrollo.
Pagina 20 di 21
LICEO SCIENTIFICO-LINGUISTICO “A. M. DE CARLO” GIUGLIANO IN CAMPANIA(NA)
8
7
Partecipa alle attività didattico-educative in modo continuo.
Si impegna in modo regolare.
Metodo di lavoro
Opera autonomamente in modo corretto.
Condotta
L’alunno rispetta le regole condivise, è collaborativo nei
confronti dei compagni e degli insegnanti; si mostra
abbastanza responsabile.
Relazionalità
Maturità affettiva
Partecipazione
Impegno
Metodo di lavoro
Condotta
Relazionalità
Maturità affettiva
6
Partecipazione
Impegno
Metodo di lavoro
Condotta
Relazionalità
Maturità affettiva
Partecipazione
5
ANNO SCOLASTICO 2013/2014
Partecipazione
Impegno
Impegno
Metodo di lavoro
Condotta
L’alunno evidenzia buone capacità di relazione.
Possiede una buona capacità di autocontrollo.
Partecipa alle attività didattico-educative con regolarità,
ma non sempre con adeguata motivazione.
Si impegna in modo costante anche se non sempre approfondisce
gli argomenti di studio.
Opera in modo globalmente autonomo.
L’alunno rispetta sostanzialmente le regole, pur essendo
moderatamente vivace; se sollecitato controlla il proprio
comportamento.
L’alunno evidenzia sostanziali capacità di relazione.
Possiede autocontrollo, ma non sempre reagisce in maniera
positiva di fronte alle difficoltà.
Partecipa sufficientemente alle attività didattico-educative,
ma spesso dietro sollecitazione degli insegnanti.
Si impegna con superficialità.
Opera in modo non sempre organizzato e proficuo.
L’alunno rispetta le regole, ma solo se continuamente
sollecitato; non sempre ha cura del materiale didattico.
L’alunno evidenzia difficoltà nei rapporti interpersonali.
Non sempre dimostra capacità di autocontrollo.
Partecipa in modo saltuario alle attività didatticoeducative.
Si impegna in modo inefficace.
Opera in modo dispersivo e poco organizzato.
L’alunno non rispetta le regole di comportamento pur se
sollecitato e richiamato; a volte mette in pericolo se stesso
ed i compagni; non rispetta il materiale scolastico, gli
arredi e le strutture.
ATTIVITA’DI RECUPERO E INTEGRATIVE
Attività di recupero
Per gli allievi più deboli saranno attivati interventi individualizzati, curricolari ed
extracurricolari (secondo i tempi e le modalità definite dal collegio dei docenti), mirati sia
al recupero di abilità specifiche di calcolo, di deduzione logica e di risoluzione di problemi,
sia all’acquisizione di un più adeguato metodo di studio.
Attività di approfondimento e di integrazione
Per vivacizzare l’interesse e la partecipazione costruttiva degli gli alunni più dotati, essi
saranno costantemente impegnati in esercitazioni a più elevati livelli di complessità e in
attività integrative di approfondimento.
In particolare, saranno sollecitati ad approfondire, mediante ricerche autonome e con l’ausilio
dei più diversificati sussidi didattici, tematiche di maggiore rilevanza, sia dal punto di vista
disciplinare che per le possibilità di applicazione in campo scientifico, economico e sociale.
Parimenti sarà incoraggiata la partecipazione a concorsi e gare disciplinari (Olimpiadi di
Fisica e di Matematica), progetti interni (ECDL, Laboratorio di Fisica).
GIUGLIANO 08.10.13
LA COORDINATRICE
Pagina 21 di 21