“Sistemi di punti materiali”
•
Finora si è parlato di “punti materiali”: è un po’ limitativo (oggetti piccoli o
“privi di struttura”). E’ opportuno estendere.
•
Il 3° Principio della dinamica ci permette di ricavare teoremi riguardanti il
moto globale di un sistema
•
Si trova che il moto “globale” di un sistema è quello di un suo punto
notevole
v
piano orizzontale
Una persona nel vagone lasciato a sè stesso non è in
grado di modificare il moto globale del sistema.
Ciò perché abbiamo un sistema isolato.
La “quantità di moto“ rimane costante.
“Sistemi di punti materiali”
Come descrivere la rotazione di un sistema, da un punto di vista dinamico?
Esiste qualcosa come la “quantità di rotazione” di un sistema?
Perché la terra non cessa di ruotare sul suo asse?
Perché la terra non cade sul sole?
In casi come questo, si osserva che in un sistema isolato
la “quantità di rotazione” rimane costante.
Come quantificare l’effetto di una forza sulla rotazione di un sistema?
es. porta
L’effetto (accelerazione angolare) di
queste forze è molto diverso
Questo è un capitolo molto generale. Le conclusioni cui si arriverà rappresentano
alcune fra le leggi più generali della fisica, la cui validità non è limitata alle leggi di Newton
Sistemi di punti materiali
Definizione di Centro di Massa o Baricentro. Punto matematico
Caso di 2 punti materiali sull’asse x (problema 1D)
O
m1
m2
x
x1
m1
x2
m2
l
d1
x cm =
d2
m 1 x1 + m 2 x 2
m1 + m 2
d 1 = x CM − x 1 =
m2
l
m1 + m 2
d 2 = x 2 − x CM =
m1
l
m1 + m 2
d1
m
= 2
d2
m1
Centro di massa o baricentro
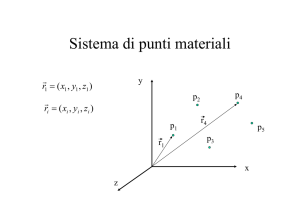
Nello spazio 3D, il baricentro di due “punti materiali”, m1 di coordinate r1 = (x1, y1,
z1), e m2, di coordinate r2 = (x2, y2, z2) ha coordinate:
x cm =
m 1 x1 + m 2 x 2
m1 + m 2
generalizzazione
a N punti:
y cm =
m1 y1 + m 2 y 2
m1 + m 2
m1 z1 + m 2 z 2
m1 + m 2
x cm =
m1 x1 + m 2 x 2 + ... + m N x N
m1 + m 2 + ... + m N
y cm =
m1 y 1 + m 2 y 2 + ... + m N y N
m1 + m 2 + ... + m N
z cm =
m1 z 1 + m 2 z 2 + ... + m N z N
m1 + m 2 + ... + m N
Vettorialmente:
r
rcm
z cm =
r
r
r
m1 r1 + m2 r2 + ... + m N rN
=
=
m1 + m2 + ... + m N
r
r
m
∑ kk
k
∑m
=
k
r
r
m
∑ kk
k
r
⇒ rcm = x cm xˆ + y cm yˆ + z cm zˆ
r
r
r
r
mTOT rcm = m1r1 + m2 r2 + ... + mN rN
mTOT
k
m k → dm
Nel caso “continuo” :
→
V
k
∑
∫
⇒
r
rcm =
1
m TOT
r
r
∫ dm
Centro di massa e simmetria
Il centro di massa giace
• nei punti di simmetria
• lungo gli assi di simmetria
• sui piani di simmetria
Il c.d.m. di un triangolo
omogeneo sta all’incrocio
delle mediane
Centro di massa di sistemi composti.
m1
m2
x cm =
x1
cdm1
cdm2
x2
m 1 x1 + m 2 x 2
m1 + m 2
Sistemi di punti materiali: forze interne e forze esterne
Sistema: Luna
FTL e FSL sono forze esterne
FLS
FSL
FTS
FTL
FLT
FST
Le forze interne hanno un’importante proprietà:
a due a due si annullano.
Sistema: Luna + Terra.
FTL e FLT sono forze interne
FST e FSL sono forze esterne
F13
F21
1
F31
3
F23
F32
2
F12
Moto del centro di massa
r
r
r
r
mTOT rcm = m1r1 + m2 r2 + .... + mN rN =
∑
r
mk rk
definizione di baricentro
k
r
r
r
r
mTOT vcm = m1v1 + m2 v2 + .... + mN v N =
∑
r
mk vk
k
r
r
r
r
mTOT acm = m1 a1 + m2 a 2 + .... + mN a N =
∑
derivando rispetto al tempo si calcola
velocità e accelerazione del c.d.m.
r
mk ak
k
r
r
r
r
r
m TOT a cm = F1 + F2 + ... + F N = F EST
Le forze interne si annullano a 2 a 2.
Teorema del moto del centro di massa
r
r
m TOT a CM = FEST
Il centro di massa si muove come un punto materiale
♦ in cui è concentrata la massa mTOT
♦ soggetto alla somma delle forze esterne
Moto del centro di massa. Esempi
Traiettorie paraboliche
Se FEST =mTOTg il moto del baricentro è parabolico (è trascurabile l’effetto dell’aria).
700.000km
cdm (450000km)
150.000.000km
sole
terra
1.99.1030kg
5.97.1024kg
Se il sistema terra sole è isolato vcm cost. Il centro
di rotazione non è il sole ma il c.d.m. terra-sole !
Quantità di moto del sistema
r
r
r
r
r
q TOT = m1 v 1 + m 2 v 2 + .... + m N v N = mTOT v cm
r
r
q TOT = mTOT v cm
quantità di moto totale
è la quantità di moto di un punto materiale di massa
mTOT coincidente con il centro di massa.
Teorema della quantità di moto
r
r
d( mTOT vcm )
r
= mTOT aCM = FEST ⇒
dt
r
r
d q TOT
= F EST
dt
La risultante delle forze esterne rappresenta la variazione della quantità di moto
rispetto al tempo.
Sistemi isolati.
Un sistema si dice isolato se non agiscono forze esterne. In generale però basta che FEST=0
Sistema: Luna
non è isolato
FSL
FLS
FTS
FTL
FLT
Sistema: Luna + Terra.
non è isolato
FST
Il sistema Sole + Terra + Luna è isolato (se si trascurano le forze degli altri pianeti)
Teorema del moto del baricentro:
Teorema della quantità di moto:
r
r
m TOT a CM = 0 ⇒ v CM = cost
r
d q TOT
r
= 0 ⇒ q TOT =
dt
cost
Sistemi isolati. Applicazioni. Urti.
Urto totalmente anelastico: le due masse restano attaccate dopo l’urto (procedono insieme)
m1
caso 1D)
cdm
v1
m2
m1
prima
m2
vCM
dopo
m1 v1 = (m1 + m 2 )v f ⇒ v f =
m1 v1
= v CM
m1 + m 2
caso 2D)
r
r
r
r
r
m1v1 + m 2 v 2 = (m1 + m 2 )v f ⇒ v f = v CM
m1
v1
vf = vcm
cdm
v2
m2
m1+m2
m1v1X + m2 v2 X = (m1 + m2 )v fX
m1v1Y + m2 v2Y = (m1 + m2 )v fY
Sistemi
Sistemi isolati
isolati
c.d.m.
m1
piano orizzontale liscio: sistema isolato.
(non se il piano è scabro o inclinato)
m2
r
FEST = 0 ⇒
F2
F1
r
a CM = 0 ⇒
v CM = cost
In un sistema isolato, il cdm (baricentro) ha moto rettilineo uniforme.
In particolare, se è in quiete, rimane in quiete.
r
r
FEST = 0 ⇒ qTOT = cost
In un sistema isolato, la quantità di moto
si conserva (è costante nel tempo).
Se il sistema in figura è isolato, inizialmente in quiete, che succede dopo la spinta?
Che relazione c’è fra v1 e v2?
v1
m1
m2
v2
cdm fisso
r
r
m 1v1 + m 2 v 2 = 0
m r
r
v 2 = − 1 v1
m2
Conservazione della quantità di moto.
r
r
m C vC + m P vP = 0
Rinculo di un cannone.
m r
r
vC = − P vP
mC
Piattaforma su superficie orizzontale liscia
m u = 70 kg
m p = 350 kg
inizialmente in quiete
vu = v p = 0
v u′ = 3 m / s → v ′p = − 0 .6 m / s
Razzo isolato e in quiete
gas ad alta velocità
posizione del c.d.m
rinculo del razzo
Esempi di urto completamente anelastico.
Un corpo di massa m1=2kg scivola su un piano orizzontale liscio, con
velocità v=5m/s. Si scontra con un corpo m2=3kg rimanendovi attaccato.
Determinare vf..
m1v
vf =
= 2m / s
m1 + m 2
Come sopra, ma il piano è scabro con µD=0.3 per entrambe le masse.
Se v=5m/s al momento dell’impatto, determinare la velocità dopo l’urto
e la distanza percorsa dal sistema prima di fermarsi.
v f = 2m / s
a = f D g = 2 .94 m / s 2 ⇒ D = 68 cm
Due auto, di massa m1=1400kg e m2=1600kg viaggiano a velocità
v1=60km/h e v2=90km/h, che formano un angolo di 90° fra loro.
Se si scontrano in un urto totalmente anelastico, determinare la velocità
del sistema subito dopo l’urto.
r
r
r
m 1 v 1 + m 2 v 2 = (m 1 + m 2 )v f
vf =
( q 12 + q 22 )
m TOT
= 15 .4 m / s
30 .3 ° risp . v 2