Sistema di punti materiali

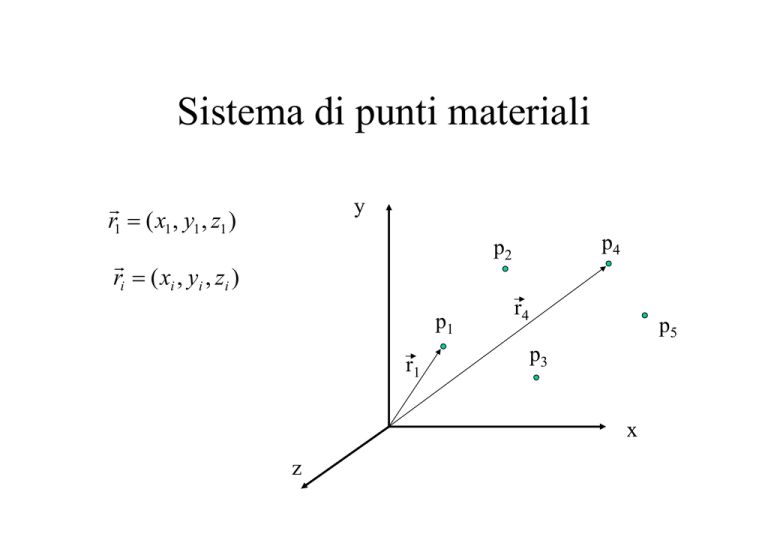
Sistema di punti materiali
r
r1 = ( x1 , y1 , z1 )
y
p4
p2
r
ri = ( xi , yi , zi )
p1
r1
r4
p5
p3
x
z
Sistema di punti ymateriali
r
r1 = ( x1 , y1 , z1 )
p2
p1
r1
Centro di Massa
p4
r4
p3
p5
x
z
Primo caso: m 1= m2= m3= …. = 1 Kg
r
rCM
r r r
r
r1 + r2 + r3 + ....... + rn
=
n
xCM
x1 + x2 + x3 + ....... + xn
=
n
yCM
y1 + y2 + y3 + ....... + yn
=
n
zCM
z1 + z 2 + z3 + ....... + z n
=
n
Sistema di punti ymateriali
r
r1 = ( x1 , y1 , z1 )
p2
p1
r1
Centro di Massa
p4
r4
p3
p5
x
z
Caso generale
r
r
r
r
r
m1r1 + m2 r2 + m3 r3 + ....... + mn rn
rCM =
m1 + m2 + m3 + ....mn
(1)
r
rCM =
xCM
m1 x1 + m2 x2 + m3 x3 + ....... + mn xn
=
m1 + m2 + m3 + ....mn
yCM
m1 y1 + m2 y2 + m3 y3 + ....... + mn yn
=
m1 + m2 + m3 + ....mn
zCM
m1 z1 + m2 z 2 + m3 z3 + ....... + mn z n
=
m1 + m2 + m3 + ....mn
r
m
r
∑ ii
∑m
i
(in forma compatta)
Sistema di punti materiali
CENTRO DI MASSA
y
p4
p2
r4
p1
r1
r
rCM
CM
p5
p3
x
z
(1)
r
rCM =
r
∑ mi ri
∑m
i
=
r
∑ mi ri
mtot
Sistema di punti materiali
Quantità di moto
y
p2
p1
r1
p4
r4
p3
p5
x
z
(2)
La quantità di moto di un sistema
di punti materiali è definita come
la somma delle quantità di moto
dei singoli punti:
r
r r
r
r
ptot = p1 + p2 + ....... + pn = ∑ pi
dove la quantità di moto di ciascun punto è
r
r
p i = mi vi
Sistema di punti materiali:
Velocità del CENTRO DI MASSA
y
p4
p2
p1 r r4 CM p5
r1 r p3
x
CM
z
Per il punto “centro di massa” possiamo
definire una velocità ed una accelerazione
come fatto (per un qualisiasi punto) in
cinematica:
r fin r iniz
r
rCM − rCM
= (se dtÆ0, abbiamo la velocità istantanea)
vCM =
dt
r fin
r fin
r fin
r iniz
r iniz
r iniz ⎤
1 ⎡ 1
(m1r1 + m2 r2 .... + mn rn − m1r1 − m2 r2 .... − mn rn )⎥ =
⎢
dt ⎣ mtot
⎦
r fin
r iniz
r fin
r iniz
r fin
r iniz
mn rn − mn rn ⎤
1 ⎡ m1r1 − m1r1
m2 r2 − m2 r2
+
+ ..... +
⎢
⎥
mtot ⎣
dt
dt
dt
⎦
Sistema di punti materiali:
Velocità del CENTRO DI MASSA
…. da cui:
r
r
r
r
1
(3) vCM =
[m1v1 + m2v2 + ..... + mn vn ] =
mtot
r
∑ mi vi
mtot
relazione formalmente identica a quella della definizione di centro
di massa, ottenibile da (1) sostituendo r (posizione) con v (velocità)
r
r
r
r
r
Riscriviamo la (3) come: mtot vCM = m1v1 + m2 v2 + ..... + mn vn = ptot
r
r
r
Ossia: (4) ptot = mtot vCM ≡ pCM
La quantità di moto di un sistema di punti materiali è pari a quella
che spetterebbe al Centro di Massa del sistema se in esso fosse
concentrata tutta la massa del sistema
Sistema di punti materiali:
accelerazione del CENTRO DI MASSA
In maniera del tutto analoga si ottiene l’espressione dell’accelerazione
del centro di massa, a partire dalla definizione:
r fin r iniz
r
vCM − vCM
=
aCM =
dt
r fin
r fin
r fin
r iniz
r iniz
r iniz ⎤
1 ⎡ 1
(m1v1 + m2 v2 .... + mn vn − m1v1 − m2 v2 .... − mn vn )⎥ =
⎢
dt ⎣ mtot
⎦
r fin
r iniz
r fin
r iniz
r fin
r iniz
mn vn − mn vn ⎤
1 ⎡ m1v1 − m1v1
m2 v2 − m2 v2
+
+ ..... +
⎢
⎥
mtot ⎣
dt
dt
dt
⎦
r
r fin r iniz
mi ai
r
r
r
r
vCM − vCM
1
∑
[m1a1 + m2 a2 + .... + mn an ] =
=
(5) aCM =
dt
mtot
mtot
Teorema del moto del centro di massa
Dividiamo le forze applicate ai punti materiali del sistema in due classi:
1) Forze interne al sistema (Fij) e 2) Forze esterne (Festi)
Consideriamo prima le forze interne:
F21
y
p2
p1
F12
F24
p4
F42
p5
p3
x
z
Per il Terzo Principio della
dinamica:
F12= - F21
F13= - F31
F14= - F41
F32= - F23
F34= - F43
F35= - F53
…………………………
Le forze interne sono a due a due uguali ed opposte !
Teorema del moto del centro di massa
Scriviamo la 2° legge della dinamica per ciascun punto materiale
costituente il sistema
r
r
⎧ F1tot = m a 1
⎪ r tot
r
⎪ F2 = m a 2
⎨
⎪ ...
⎪ Fr tot = m ar
n
⎩ n
r
⎧ r est
⎪ F1 + F12 +
⎪ r
⎪⎪ F est + Fr +
2
21
⎨
⎪ ...
⎪
⎪ Fr est + Fr +
n1
⎪⎩ n
r
r
r
r
d p1
F13 + .... + F1 n = m a 1 =
dt
r
r
r
r
dp2
F 23 + .... + F 2 n = m a 2 =
dt
r
r
r
r
dpn
F n 2 + .... + F n n − 1 = m a n =
dt
sommando membro a membro le n equazioni del sistema, ricordando
che le forze interne sono a due a due uguali ed opposte,rsi ottiene:
r est
r
r
r
r
dpi
Ftot = m1a1 + m2 a2 + ..... + mn an = ∑ mi ai = ∑
dt
r est r est r est
r est
r est
dove Ftot = F1 + F2 + ..... + Fn = ∑ Fi
Teorema del moto del centro di massa
r
r fin r iniz r fin r iniz
r fin r iniz
r est
dpi p1 − p1 + p2 − p2 + ..... + pn − pn
Ftot = ∑
=
=
dt
dt
r fin r iniz
r
ptot − ptot
dptot
=
=
dt
dt
r est dpr tot
Pertanto: (6) Ftot =
dt
r est dpr CM
od in maniera equivalente: (6’) Ftot =
dt
r est
oppure ancora: (6’’) F = mar
tot
CM
attribuendo al centro
di massa tutta la massa
del sistema
Teorema del moto del centro di massa
Le equazioni (6’) o (6’’) ci dicono che, se attribuiamo al centro di
massa tutta la massa del sistema, la dinamica di questo punto è
governata dalla 2° legge di Newton, scritta considerando solo
le forze esterne (tutte) ed ignorando le forze interne.
r est dpr CM
Ftot =
dt
r est
r
Ftot = maCM
Ad esempio, il moto del centro di massa
di una palla di cannone che esplode a metà
della sua traiettoria è sempre parabolico,
anche dopo l’esplosione.
Teorema di conservazione della
quantità di moto
L’equazione (6) è particolarmente utile quando la risultante delle
forze esterne è nulla. Ad esempio, per un sistema isolato, ciascuna
delle Forze esterne è nulla (Fest1= Fest2=… =Festn=0).
r
dptot
=0
dt
r
ptot = costante
In un sistema isolato, od un sistema tale che la risultante delle forze
esterne sia nulla, la quantità di moto si conserva.
Per le applicazioni e gli esercizi, fare riferimento al libro di testo ed agli
appunti delle lezioni.