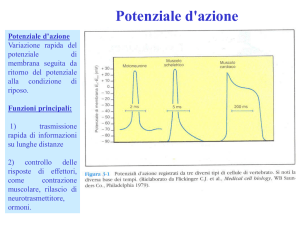
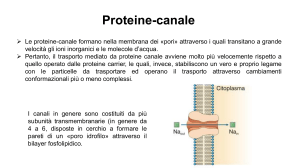
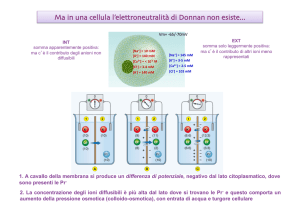
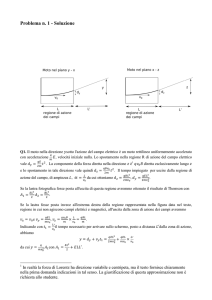
Equazione di Goldman-Hodgkin-Katz
Consideriamo una membrana avente un canale permeabile a uno ione di tipo
A. Siano [A]in e [A]out le concentrazioni dello ione all’interno e all’esterno
della membrana. Se z è la direzione del canale, perpendicolare alla membrana, e [A] è la concentrazione in funzione di z, il flusso di ioni all’interno
del canale è uguale a
d[A]
+ µA nA qE[A],
dz
dove DA è la diffusività, µA la mobilità, nA la valenza dello ione di tipo A,
q la carica elementare, ed E il campo elettrico all’interno del canale ionico.
Il primo è il termine di Fick, che esprime il flusso dovuto al gradiente di
concentrazione. Il secondo invece è il flusso determinato dal campo elettrico.
Nell’ipotesi che il campo elettrico sia costante lungo il canale, possiamo
scrivere il potenziale di membrana come V = EL, dove L è la lunghezza del
canale. Integrando quest’equazione per separazione di variabili dall’interno
all’esterno della membrana, otteniamo che la corrente determinata dagli ioni
di tipo A è data da
[A]out − [A]in exp (nA qV /kB T )
V,
iA = nA qSJA = PA
1 − exp (nA qV /kB T )
JA = −DA
µ n2 q 2 S
dove PA = A LA
è la permeabilità del canale ionico, e abbiamo usato la
relazione di Stokes-Einstein DA = kB T µA .
Imponendo che la corrente si annulli otteniamo l’equazione di Nernst
kB T
[A]out
VA =
ln
,
nA q
[A]in
che esprime il potenziale di equilibrio (o di inversione) per gli ioni di tipo A.
Se abbiamo diversi tipi di ioni, A, B, etc..., e imponiamo che la corrente
totale si annulli, nell’ipotesi che gli ioni abbiano tutti valenza +1 otteniamo
che il potenziale di equilibrio complessivo è dato da
kB T
PA [A]out + PB [B]out + · · ·
ln
.
V =
q
PA [A]in + PB [B]in + · · ·
Se uno ione ha valenza −1, bisognerà per quello ione scambiare out con in.
Se invece ci sono ioni con valenza +2 o −2, bisognerà risolvere un’equazione
quadratica.