1
Bipoli Elettrici
Esercitazioni aggiuntive
Esercizio
1.1
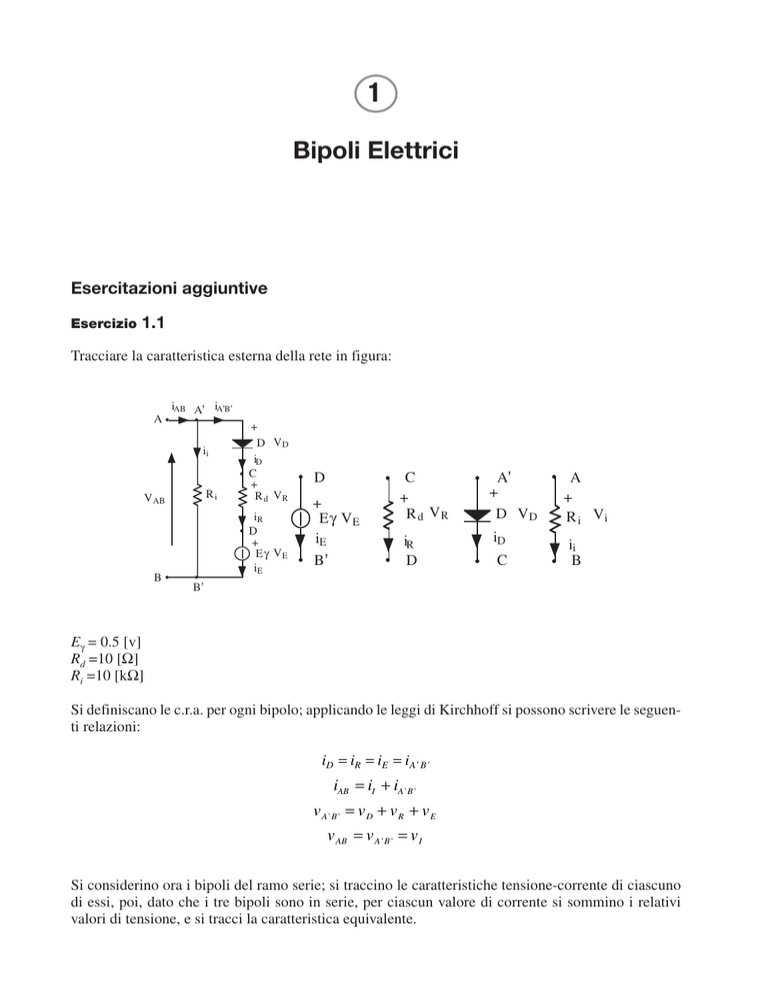
Tracciare la caratteristica esterna della rete in figura:
A
iAB Aʼ iAʼBʼ
ii
Ri
VAB
B
+
D VD
iD
C
+
R d VR
iR
D
+
Eγ VE
iE
D
+
Eγ VE
iE
Bʼ
C
+
R d VR
Aʼ
+
D VD
iR
D
iD
C
A
+
R i Vi
ii
B
Bʼ
Eg = 0.5 [v]
Rd =10 [W]
Ri =10 [kW]
Si definiscano le c.r.a. per ogni bipolo; applicando le leggi di Kirchhoff si possono scrivere le seguenti relazioni:
i D = i R = iE = i A ' B '
vA 'B ' = vD + vR + vE
v AB = v A ' B ' = v I
iAB = iI + iA ' B '
�
� ramo serie; si traccino le caratteristiche tensione-corrente di ciascuno
Si considerino ora i bipoli del
di essi, poi, dato che i tre bipoli
� sono in serie, per ciascun valore di corrente si sommino i relativi
valori di tensione, e si tracci la caratteristica equivalente.
2
Bipoli Elettrici
VR [v]
VD [v]
10
0
iD [A]
0
1
iR [A]
VE [v]
0.5
0
iE [A]
VAʼBʼ [v]
1.5
0.5
0
0.1
iAʼBʼ [A]
Successivamente si disegni la caratteristica relativa al ramo Ri, che è:
Vi [V]
10
0
1 . 10 -3
ii [A]
3
esercitazioni
Infine la caratteristica richiesta deriva dalla composizione in parallelo di quelle ralative al ramo serie
ed al resistore Ri; per ciascun valore di tensione occorre sommare le corrispondenti correnti.
La caratteristica dell’intera rete è qui riportata:
VAB [v]
0.6
0.5
0
iAB [A]
0.01
Si osservi che la pendenza del ramo corrispondente ad Ri è stata arbitrariamente aumentata per una
maggiore chiarezza del disegno.
Esercizio 1.2
Dato il circuito in figura ricavare la caratteristica esterna: vAB = f(iAB).
A
iAB
E
I
R
B
I = 1 [A]
R = 1 [W]
Si stabiliscano le c.r. di ogni bipolo.
E
iI
A
iD
VI
VD
E
E
iR
VR
B
Applicando le leggi di Kirchhoff si trovano le seguenti relazioni:
iAB = iD
iAB = iI + iR
vAB = vD + vED
vEB = vR = vI
B
4
Bipoli Elettrici
Si traccino le caratteristiche tensione-corrente per ciascun bipolo:
VD [v]
0
VI [v]
-I
iD [A]
0
iI [A]
VR [v]
1
0
1
iR [A]
Dato che I ed R sono in parallelo per ciascun valore di tensione si devono sommare le correnti. Si
ottiene:
VEB [v]
1
0
iAB [A]
-1
La caratteristica vAB = f(iAB) si ottiene componendo in serie l’ultima tracciata con quella del diodo:
vAB = vD + vEB
5
esercitazioni
Si ricava
VAB [v]
1
0
iAB [A]
-1
Esercizio 1.3
Scrivere le leggi di Kirchhoff per le correnti e le tensioni per la rete di figura:
A
1
B
3
D
4
5
E
F
6
7
G
C
2
8
9
H
10
I
La rete è composta da 10 rami; essa contiene 9 nodi, di cui 6 impropri. Le maglie sono 3.
Nodi: A, B, C, D, E, F, G, H, I.
Maglie: ABCFED; DEFIHG; ABCFIHGD.
Nella seguente figura è riportato il grafo della rete in cui è stata eseguita l’operazione di orientamento
dei singoli rami che, come è noto, equivale ad assumere i versi positivi delle correnti. Se, inoltre, per
comodità si decide di assumere nella rete anche le condizioni di riferimento associate per i bipoli
passivi, si osserva che automaticamente vengono stabiliti anche i versi delle polarità delle tensioni
come è indicato a fianco della figura successiva.
6
Bipoli Elettrici
Si ottiene così il seguente schema:
A
i3
V3
1
3
7
B
V1
D i
i7
V7
i
5
9
i
C
i4
V2
E i
V5
G i
2
6
V6
Hi
V9
10
V4
4
F
i8
V8
8
I
V10
EQUAZIONI AI NODI
A) i1 − i3 = 0
B) i2 − i1 = 0
C) i4 − i2 = 0
D) i3 − i5 − i7 = 0
E) i5 − i6 = 0
F) i6 + i8 − i4 = 0
G) i7 − i9 = 0
H) i9 − i10 = 0
I) i10 − i8 = 0
EQUAZIONI ALLE MAGLIE:
ABCFED) − v1 − v2 − v4 − v6 − v5 − v3 = 0
DEFIHG) v5 + v6 − v8 − v10 − v9 − v7 = 0
ABCFIHGD) − v1 − v2 − v4 − v8 − v10 − v9 − v7 − v3 = 0
Ovviamente, come verrà espresso più chiaramente nel prossimo capitolo, nelle equazioni alle maglie sopra scritte sarebbe opportuno esprimere le tensioni di ramo in funzione delle relative correnti, ciò facendo uso delle r equazioni costitutive scritte per tutti i rami della rete, al fine di risolvere
il circuito.
7
esercitazioni
Esercizio 1.4
Scrivere le leggi di Kirchhoff per le correnti e le tensioni per la rete di figura:
2
1
3
4
5
6
7
8
La rete è composta da 8 rami; contiene 5 nodi (di cui 1 improprio) e 12 maglie.
Anche in questo caso, nella seguente figura è riportato il grafo della rete in cui è stata eseguita l’operazione di orientamento dei singoli rami che, come è noto, equivale ad assumere i versi positivi delle
correnti. Se, inoltre, per comodità si decide di assumere nella rete anche le condizioni di riferimento
associate per i bipoli passivi, si osserva che automaticamente vengono stabiliti anche i versi delle
polarità delle tensioni come è indicato a fianco della figura successiva.
Si scelga arbitrariamente, inoltre, il verso di percorrenza antiorario per tutte le maglie.
Si ottiene così il seguente schema:
EQUAZIONI AI NODI:
A) i1 − i2 = 0
B) i3 + i8 − i1 − i4 = 0
C) i2 + i6 + i5 − i3 = 0
D) i4 + i7 − i5 = 0
E) − i6 − i7 − i8 = 0
i2
A
i1
V2
1
V1
2
i3
B
V3
i6
i5
i4
V4
C
3
4
5
i7
D
6
V5
7
V7
8
V8
i8
V6
E
8
Bipoli Elettrici
EQUAZIONI ALLE MAGLIE
ACB) v2 + v3 + v1 = 0
BCD) − v3 − v5 − v4 = 0
CED) − v6 + v7 + v5 = 0
DEB) − v7 + v8 + v4 = 0
ACDB) v2 − v5 − v4 + v1 = 0
BDCE) v4 + v5 − v6 + v8 = 0
BCED) − v3 − v6 + v7 − v4 = 0
BCE) − v3 − v6 + v8 = 0
BCDE) − v3 − v5 − v7 + v8 = 0
ACEDB) v2 − v6 + v7 − v4 + v1 = 0
ACDEB) v2 − v5 − v7 + v8 + v1 = 0
ACEB) v2 − v6 + v8 + v1 = 0
Esercizio 1.5
Scrivere le leggi di Kirchhoff per le correnti e le tensioni per la rete di figura:
1
A
B
2
5
E
C
3
6
8
13
F
D
4
7
9
G
10
H
11
12
La rete è composta da 13 rami; ha 8 nodi (di cui 2 impropri) e 27 maglie.
Procedendo ancora in maniera analoga, si assegnino arbitrariamente i versi delle correnti nei
diversi rami, e si indichino i versi delle tensioni su di essi, determinati applicando le condizioni di
riferimento associate (convenzioni per gli utilizzatori in questo caso).
Si stabilisce arbitrariamente, inoltre, il verso di percorrenza antiorario per ciascuna maglia.
EQUAZIONI AI NODI:
A) i1 + i2 − i5 = 0
B) i3 + i6 − i2 = 0
C) i4 − i1 − i3 = 0
9
esercitazioni
D) i7 − i4 = 0
E) i5 − i8 − i13 = 0
F) i8 + i13 − i6 − i9 − i11 − i12 = 0
G) i9 − i10 = 0
H) i10 + i11 + i12 − i7 = 0
V1
i1
V2
i2
A
3
i3
C
V4
4
i4
D
i7
i6
5
E
V3
B
2
i5
V5
1
6
i8
8
F
7
V6
i9
i13 V8
13
i
G 10
9
V9 i11
V13
11
i12 V11
12
V12
EQUAZIONI ALLE MAGLIE:
ACB) v1 − v2 − v3 = 0
ABFE) v2 + v5 + v8 + v6 = 0
BCDHGF) v3 − v6 + v9 + v10 + v7 + v4 = 0
FGH) − v10 − v9 + v11 = 0
ACDHGFB) v1 − v2 − v6 + v9 + v10 + v7 + v4 = 0
ACDHFB) v1 − v2 − v6 + v11 + v7 + v4 = 0
ACDHGFE) v1 + v5 + v8 + v9 + v10 + v7 + v4 = 0
ACDHFE) v1 + v5 + v8 + v11 + v7 + v4 = 0
ABCDHGFE) v2 + v5 + v8 + v9 + v10 + v7 + v4 + v3 = 0
ABCDHFE) v2 + v5 + v8 + v11 + v7 + v4 + v3 = 0
BCDHF) v3 − v6 + v11 + v7 + v4 = 0
FGH) − v10 − v9 + v12 = 0
ACDHFB) v1 − v2 − v6 + v12 + v7 + v4 = 0
ACDHFE) v1 + v5 + v8 + v12 + v7 + v4 = 0
ABCDHFE) v2 + v5 + v8 + v12 + v7 + v4 + v3 = 0
10
V10
V7
H
10
Bipoli Elettrici
BCDHF) v3 − v6 + v12 + v7 + v4 = 0
FH) − v11 + v12 = 0
ABFE) v2 + v5 + v13 + v6 = 0
ACDHGFE) v1 + v5 + v13 + v9 + v10 + v7 + v4 = 0
ACDHFE) v1 + v5 + v13 + v11 + v7 + v4 = 0
ABCDHGFE) v2 + v5 + v13 + v9 + v10 + v7 + v4 + v3 = 0
ABCDHFE) v2 + v5 + v13 + v11 + v7 + v4 + v3 = 0
ACDHFE) v1 + v5 + v13 + v12 + v7 + v4 = 0
ABCDHFE) v2 + v5 + v13 + v12 + v7 + v4 + v3 = 0
EF) − v8 + v13 = 0
ACBFE) v1 + v5 + v8 + v6 − v3 = 0
ACBFE) v1 + v5 + v13 + v6 − v3 = 0
Esercizio 1.6
Determinare il punto di lavoro della rete rappresentata in figura:
R0
A
+
E0
R
i
VR
iR
B
E0 = 5 [v]
R0 = 1.5 [W]
vR = 0.5 ⋅ iR2 iR ≥ 0
vR = 0 iR < 0
Si disegnino le caratteristiche dei tre singoli bipoli sui rispettivi piani di definizione; dopo aver scritto
le leggi di Kirchhoff per le tensioni e per le correnti si tracci la caratteristica composta del bipolo
serie E0 – R0.
Quindi si disegni la caratteristica del resistore non lineare R sul piano (IR, VR).
Osservando che le due caratteristiche possono essere tracciate sullo stesso piano di lavoro in
base ai principi di Kirchhoff, tarando opportunamente gli assi, la relativa intersezione rappresenta il
punto di lavoro della rete individuando i valori della corrente che circola nell’unica maglia e della
tensione VAB.
Lo stesso problema può essere risolto anche nel seguente modo: si assegnino i versi delle correnti e delle tensioni come in figura; si traccino la caratteristica composta della serie E0 – R0 e quella
del resistore R; si rappresenti, infine, la caratteristica i cui punti si ottengono fissando un valore di
tensione, trovando le correnti ad esso corrispondenti dai due precedenti grafici, e calcolandone la
somma in base al principio di Kirchhoff per le correnti.
Quando, per un particolare valore di tensione, la somma delle due correnti è nulla, si è trovato
il punto di lavoro.
11
esercitazioni
Ciò si spiega, fisicamente, osservando che in una serie di bipoli il modulo della corrente, a parte
le assegnazioni di verso (arbitrarie) su ciascuno di essi, deve essere uguale per ogni elemento; pertanto, avendo stabilito versi opposti per le correnti nella serie E0 – R0 e nel resistore R, in corrispondenza
del punto di lavoro della rete la loro somma deve essere nulla.
Esercizio 1.7
Determinare il punto di lavoro della rete rappresentata in figura:
R0
C
R1
A
+
+
R
E0
E1
i1
B
E0 = 5 [v]
E1 = 8 [v]
R0 = 1.5 [W]
R1 = 2 [W]
vR = 0.5 ⋅ iR2 iR ≥ 0
vR = 0 iR < 0
Si definiscano i versi delle tensioni e delle correnti secondo le condizioni di riferimento associate per
gli utilizzatori per i seguenti bipoli: R, R0, E0, e la serie R1 – E1.
C
A
A
A
R1
+
+
VE
E0
R0
VR0
iE
B
R
VR
iR0
C
E1
V1
iR
B
i1
B
Applicando le leggi di Kirchhoff si trovano le relazioni:
iAB = iR0 = iE = − iR − i1
vAB = vR = vR0 + vE = v1
( )
Si disegnino le caratteristiche dei bipoli, e si compongano in serie la vR0 = f1 iR0 e la vE = f2 ( iE ) ,
sommando le tensioni dei due bipoli relative a ciascun medesimo valore di corrente. Si ottiene così
la caratteristica vAB = f iAB .
Si rappresenti ora la funzione vAB = f iAB + iR + il ; essa si ottiene fissando un valore di tensione, determinando dalle caratteristiche le tre correnti, e calcolandone la somma, e ripetendo poi queste
operazioni per un numero sufficiente di punti. Quando, per un dato valore di tensione, la somma
delle tre correnti è uguale a zero, sono verificate contemporaneamente le due leggi di Kirchhoff, e si
determina il punto di lavoro del circuito.
( )
(
)
12
Bipoli Elettrici
(
)
Si riporta di seguito il grafico della funzione vAB = f iAB + iR + il :
VAB [v]
4
3,5
3
2,5
2
1,5
1
0,5
0
-8
-7
-6 -5 -4 -3 -2
Somma delle correnti [A]
-1
0
Esercizio 1.8
Determinare le tensioni ai capi dei resistori per ciascuno dei tre circuiti mostrati in figura.
Calcolare la potenza dissipata da ogni resistore e da dove viene generata questa potenza, calcolando il contributo dovuto al generatore di tensione ed a quello di corrente.
I1
+
E
A
I2
+
I3
VR
R
R
+
I E
I
B
1) E = 2 [V]; I = 1 [A]; R = 3 [W].2) E = 2 [V]; I = 1 [A]; R = 3 [W]
IE
+
E
R2
A
+
IR
VR
R1
B
3) E = 2 [V]; I = 1 [A]; R1 = 1 [W]; R2 = 3 [W]
I
esercitazioni
1) Applicando le leggi di Kirchhoff si ottiene:
i1 + i2 = i3
i2 = 1 [A]
vR = E = vI = 2 [v]
dalla relazione costitutiva del resistore si ha:
2v
= 0.667 [A]; quindi si ottiene:
3 Ω
i1 = i3 − i2 = −1 + 0.667 = −0.33 [A]
i3 =
PgE = (−0.333 ⋅ 2 ) = −0.667 [W] Assorbe;
PR = I 2 R = 1.33 [W] Assorbe;
PgA = IVI = 2 [W] Eroga.
2) I = 1 [A]; la tensione ai capi del resistore è:
risulta, allora:
V = RI = 3 ⋅ 1 = 3 [v]
VI = 5 [v]
PgI = 5 ⋅ 1 = 5 [W]
PgV = 2 [W] Assorbe;
PJ = 3 ⋅ 1 = 3 [W] Assorbe.
3) Applicando le leggi di Kirchhoff si ottiene:
IE + I = IR
I = 1 [A]
VR1 = 2 [v]; la corrente su R1 vale:
IR =
2
= 2 [A]
1
si calcola allora:
I E = 2 − 1 = 1 [A]
Pg = 2 [W]
PR1 = RI R2 = 4[W ]
VR2 = 3 [v]
PR2 = 3 ⋅ 1 = 3 [W]
VI = 3 + 2 = V = 5 [v]
PgI = 5 [W]
13
14
Bipoli Elettrici
Esercizio 1.9
Dato il seguente circuito:
R3
I3
R2
A
I1
+
E
I2
R1
B
calcolare il valore delle resistenze R1 e R2 e la fem ai capi del generatore di tensione E sapendo che:
R3 = 2 [W]
PR1 = 108 [W]
PR2 = 54 [W]
PR3 = 162 [W]
Il bilancio delle potenze per il circuito dato, si esprime con la relazione:
EI 3 = R1 I12 + R2 I 22 + R3 I 32 ; risulta anche che:
I 3 = I1 + I 2 ; posto che:
R3 I 32 = 162 [W] si calcola:
PR3
I3 =
R3
=
162
= 9 [A]; poiché:
2
EI 3 = 108 + 54 + 62 = 324 [W] si calcola la tensione del generatore:
E=
324
= 36 [v] da cui:
9
VAB = E − R3 I 3 = 36 − 2 ⋅ 9 = 18 [A] ed infine:
2
VAB
= 108 [W];
R1
R1 =
18 2
= 3 [W];
108
2
VAB
= 54 [W];
R2
R2 =
18 2
= 6 [W].
54
15
esercitazioni
Esercizio 1.10
Risolvere la rete rappresentata in figura ed effettuare il bilancio delle potenze.
IE
I1
A
+
E
+
IR
VR
R
I
B
E = 1 [v]
R = 1 [W]
I = 2 [A]
Si stabiliscano su ciascun bipolo i versi delle tensioni e delle correnti secondo le condizioni di riferimento associate per gli utilizzatori e per i generatori, rispettivamente.
Si scrivano le leggi di Kirchhoff per le tensioni e per le correnti, trovando le seguenti relazioni:
VAB = VE = VR = VI
IR − IE − II = 0
Poi:
VE = E ∀I
VR = RI R
I I = I ∀VI
E = RI R
si calcola così:
IR =
E 1
= = 1 [A]
R 1
I E = I R − I I = I R − I = 1 − 2 = −1 [A]
Con riferimento alle potenze, per questo circuito si ha:
3
i =1
i =1
∑ Pi = ∑ Vi Ii
3
PE = VE I E = EI E = 1 ⋅ ( −1) = −1 [W]
PE < 0 ⇒ il generatore assorbe potenza.
PR = VR I R = EI R = 1 ⋅ 1 = 1 [W]
16
Bipoli Elettrici
PR > 0 ⇒ il resistore (utilizzatore) assorbe potenza.
PI = VI I I = EI = 1 ⋅ 2 = 2 [W]
PI > 0 ⇒ il generatore eroga potenza.
Il bilancio delle potenze si può quindi scrivere come:
3
∑ Pi = PE − PR + PI = −1 − 1 + 2 = 0
[W].
i =1
Si noti che in quest’ultima equazione PR < 0 perchè il resistore dissipa potenza.
Esercizio 1.11
Tracciare la caratteristica del bipolo equivalente alla rete seguente:
A
iAB
Aʼ
+
E
D
R2
VAB
R1
iAʼC
iAC
C
R3
iAB
B
R1 = 8 [W]
R2 = 6 [W]
R3 = 6 [W]
E = 3 [V]
Si proceda con il metodo grafico.
Si traccino le caratteristiche del resistore R1 e del generatore E:
VDC [v]
8
VAʼD [v]
3
0
1
iAC [A]
0
iAC [A]
esercitazioni
17
La caratteristica complessiva della serie R1 – E risulta:
VAʼC [v]
3
-0.375
0
iAC [A]
Si ha:
iAB = iAC + iA’C.
La caratteristica del resistore R2 è:
VAʼC [v]
6
0
1
iAʼC [A]
La caratteristica del parallelo tra la serie R1 – E ed R2 risulta:
VAʼC [v]
3
-0.375
0.5
iAB [A]
La caratteristica del resistore R3 è uguale a quella di R2; per tracciare la caratteristica del bipolo
equivalente alla rete data basta comporre in serie l’ultima ricavata con quella di R3:
18
Bipoli Elettrici
VAB [v]
6
-0.375
-2.25
iAB [A]
0.5
Esercizio 1.12
Tracciare la caratteristica del bipolo equivalente alla rete seguente:
A
R1
R2
+
E
R3
B
R1 = 6 [W]
R2 = 6 [W]
R3 = 10 [W]
E = 3 [V]
Si proceda con il metodo grafico.
Si segua un procedimento simile a quello relativo all’esercizio precedente indicando, ad esempio, i
nodi e le correnti come nel seguente schema:
iAB
A
VAB
Aʼ
iAʼC
R1
R2
iAC
D
E
+
C
R3
B
iAB
19
esercitazioni
Esercizio 1.13
Con riferimento al seguente circuito dire se i dati sono sufficienti per valutare la corrente in R3,e nel
caso affermativo valutare tale corrente:
R2
R4
+
+
E2
R3
E1
R5
R1
PerogE1 = PerogE2 = 50 [W]
PassR1 = PassR4 = 18 [W]
PassR2 = PassR5 = 12 [W]
R3 = 10 [W]
Dal bilancio delle potenze:
PEerog
+ PEerog
= PRass
+ PRass
+ PRass
+ PRass
+ PRass
1
2
3
4
5
1
2
In generale sussiste la relazione:
PRass
= Ri I R2i ;
i
dalle precedenti relazioni si ottiene allora:
PRass
= 40 [W]
3
I R3 =
PRass
3
R3
= 2 [A].
Esercizio 1.14
Nel circuito lineare tempo invariante mostrato in figura la tensione e la corrente dei corrispondenti
generatori sono rispettivamente pari a: v(t) = Ae- at; i(t) = Bcoswt, dove A, B, a, w sono costanti.
Calcolare la tensione sull’induttanza L, vL(t), e la corrente sulla capacità C, iC(t).
v(t) +
R
L1
C
L
i(t)
iC(t)
vL(t)
iL(t)
20
Bipoli Elettrici
Dalle relazioni costitutive dell’induttore e del condensatore si ha:
vL (t ) = L
di (t )
diL (t )
=L
= − LBω sin ω t [v]
dt
dt
iC (t ) = C
dvC (t )
= − ACα e−α t [A]
dt












