DIMOSTRAZIONE
Dimostrazione delle FORMULE (1.13) e (1.14)
Resistenza equivalente serie
Supponendo di avere n resistenze R1, R2, ..., Rn, collegate in serie ad un generatore di
tensione, per definizione la corrente deve essere uguale in tutti i componenti.
Le tensioni ai capi di ogni resistore sono date dalla legge di Ohm:
V1 = R1I; V2 = R2I; ... Vn = RnI
Per il secondo teorema di Kirchhoff la caduta di tensione totale è data dalla somma
delle singole tensioni:
VAB = V1 + V2 + ... + Vn = R1I + R2I + ... + RnI
e raccogliendo I
VAB = (R1+R2 + ... + Rn)I
La serie equivale quindi ad una resistenza di valore pari alla somma delle resistenze:
Req = R1 + R2 + ... + Rn
VAB
I
A
A
R1
R2
R3
V1
V2
V3
Req = R1 + R 2 + R 3
B
VAB
I
I1
R1
I2
R2
1
1
1
1
=
+
+
R eq
R1 R 2 R 3
A
B
I3
B
R3
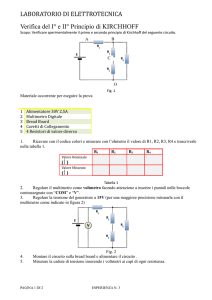
FIGURA 1 Resistori collegati A) in serie e B) in parallelo.
Resistenza equivalente parallelo
In questo caso è la tensione VAB che è uguale su tutti i resistori, mentre le correnti
valgono:
I1 =
VAB
;
R1
I2 =
VAB
R2
...
In =
VAB
Rn
Per il primo teorema di Kirchhoff la corrente totale I è data dalla somma delle singole
correnti:
1
1
1
V
V
V
)
I = I1 + I2 + ... + In = AB + AB + ... + AB = VAB ( +
+ ... +
R1
R2
Rn
R1 R2
Rn
dal confronto con la legge di Ohm si deduce che il parallelo equivale ad una resistenza di valore
Req =
1
1
1
1
+
+ ... +
R1 R2
Rn
Questo file costituisce un approfondimento online dei corsi di elettrotecnica ed elettronica
di Stefano Mirandola - © 2012 Zanichelli Editore SpA, Bologna [6126]
1