6.
FORZA DEVIANTE TERRESTRE.
Una causa di spostamento della nave dalla rotta è la forza deviante terrestre o forza composta di
Coriolis (detta anche di Ferrell).
Tutti i mobili della Terra, venti, correnti, iceberg, navi, corpi balistici… si muovono in un sistema
esso stesso in movimento, la Terra col suo moto rotatorio. Pertanto i mobili sono soggetti ad una forza
apparente, non reale. Non si capirebbero i versi di rotazione del vento quando si avvicina al centro di
una depressione: senso antiorario in latitudine. φ Nord, senso orario in φ Sud. Tale forza (studiata
bene in Meteorologia) è ortogonale alla traiettoria istantanea del mobile: sulla sinistra nell’emisfero
Sud, sulla destra nell’emisfero Nord, nulla all’equatore. La sua espressione è:
Fd = M ⋅ (2Vρsenφ) (a)
M massa del mobile (nave, nel nostro caso), V la sua velocità, ρ la velocità angolare terrestre
(72,92 ⋅ 10 – 6 rad/s) φ la latitudine. La forza deviante Fd è massima ai poli.
Alla forza Fd la nave oppone la resistenza traversale R: R = 0,5·KωAVt2 (b)
K è il coefficiente di resistenza allo spostamento trasversale che avviene con velocità Vt; nel
sistema MKS K ha il seguente valore numerico: K = 1,15; ω è la densità del mare; A è l’area della
superficie laterale di carena (A = L⋅i, con L lunghezza ed i immersione). Sia α il coefficiente di
finezza totale della nave, l la larghezza; M massa nave, è data da ωα(L⋅l⋅i).
M2Vρsenϕ
Dall’uguaglianza R = Fd si ricava Vt . Vt =
(c)
0,5 KωA
Dopo le sostituzioni delle espressioni e l’elisione dei termini comuni si ottiene:
α ⋅ l ⋅ 2Vρsenϕ
(d)
0,5 ⋅ 1,15
Eseguendo il rapporto Vt / V si ottiene il valore di tangente di δc (v. Fig. 11).
Sostituendo il valore di ρ abbiamo l’espressione della deviazione di Coriolis δc :
l ⋅ senϕ
tang δc = 0,0159 ⋅ α ⋅
(e )
V
Per le grandi navi, di T.S.L. > 60.000, si può assumere il valore medio α = 0,95
Per le navi medie, di T.S.L. comprese tra 60.000 e 10.000, si può assumere α = 0,80
l ⋅ senϕ
l ⋅ senϕ
tang δc = 0,0155 ⋅
(f)
tang δc = 0,0142 ⋅
(g).
V
V
Vt =
l in metri; V in metri al secondo. L’angolo di deviazione δc aumenta con la larghezza l della
nave, con il diminuire della velocità e con il crescere della latitudine φ.
Seguono le formule algebriche di conversione (9.VII) e di correzione (10.VII):
Pv = Rv - δc
(9.VII)
Rv = Pv + δc
(10.VII)
δc: + in φ Nord
- in φ Sud.
I Esempio: φ 45°N/S . Calcolare le Pv per seguire rotta 100°. La nave è grande (l = 58m) e
procede con velocità 12 nodi (V = 6,17 m/s). I risultati sono: δc ± 2,3°.
Pv = 97,7° in latitudine Nord
Pv = 102,3° in latitudine Sud.
II Esempio: φ 47°45', l = 20m, α = 0,70, V = 5,144m/s (10 nodi). Calcolare δc . Ris. 1,3°.
III Esempio: una grande nave (l = 54 m) intende seguire Rv 300° con Veff 13 nodi in zona di φm
40°N - λ 170°E. C’è corrente e vento (ldr + 3°; lsc -1°). Calcolare la Pv.
Risultati: δc + 2° Pv 296°.
IV Esempio. Una nave media (l = 26m) in φ ∼60°S, procede con Pv 50° Vp 6 nodi in zona di vento
e corrente contrastanti che non alterano gli elementi di moto. Determinare Rv.
Risultati: δc = - 2,2° , Rv 47°,8 ; Veff 6,0044 nodi (6/cos δc) ∼ invariabile.
La tabella dà δc per due navi di larghezza l 50 m (α 0,95) e 25 m (α 0,80, rigo sottostante).
172
CAP. VII
20 nodi
1°.1
13 nodi
1°.4
6 nodi
2°.1
0°.7
----------1°.6
0°.9
----------2°.0
1°.4
-------2°.9
1°.0
----------1°.8
1°.3
----------2°.3
1°.9
-------3°.3
1°.2
1°.5
2°.2
φ 20°
-------φ 40°
-------φ 60°
Nota: nei calcoli le V vanno espresse in m/s.
Fig. 11.
Deviazione δc di Coriolis (φN).
V Esempio. Calcolare il presumibile scarto dalla “rotta” dopo 12 ore di navigazione di una grande
nave di 50 metri di larghezza che in latitudine intorno a 25° Sud procede con V 12,5 nodi e che
trascura la δc Coriolis.
Risultati: δc - 1°.6; (m = 150 miglia); scarto s = 4,2 miglia, circa, a sinistra.
Notizie complementari. “Correva” l’anno 1959; la petroliera S.S. Veedol (65000 TSL) navigava
dal Golfo Persico verso Delaware-Philadelphia, via Capo di Buona Speranza, con velocità economica
12,50 nodi (in un periodo di crisi del mercato dei noli). Nell’Atlantico i PN delle osservazioni stellari
ai crepuscoli si susseguivano ogni 10-14 ore, ogni 11-13 ore… circa e tali PN risultavano tutti discosti
dalla rotta, mediamente, di ∼ … 4; 3,5; 3; 2,5 … miglia sulla sinistra, via via che dal Capo la nave si
avvicinava all’Equatore. Superata la Linea la tendenza s’invertì: … 2; 2,5; 3; 3,5; 4; 4,5 … miglia
circa a dritta della rotta. Poiché ad ogni PN si correggeva la rotta per tenere conto della corrente e del
vento, non si riuscì a dare un’interpretazione del singolare fenomeno.
Nel 1966, in un convegno sulla Navigazione al Nautico “Cappellini” di Livorno conobbi l’egregio
professore Mumolo al quale riferii quell’episodio di navigazione. La risposta fu: “non hai letto sulla
rivista Navigation di qualche mese fa un articolo sulla “deriva” della supertanker Manhattan, un
“mammut” che, grazie all’ausilio di rompighiacci aveva effettuato il primo transito tra banchisa e
ghiacci del Canada e dell’Alaska, il fatidico passaggio a Nord-Ovest: deriva (Earth drift) di 3, 4 …
gradi.
I sistemi inerziali e quelli non inerziali. Nello studio della Fisica il I Principio della Dinamica,
Principio d’Inerzia, dice: un corpo persevera nel suo stato di quiete o di moto rettilineo uniforme.
Viene così commentato: se il corpo non è soggetto a forza la sua velocità vettoriale (modulo scalare
e/o direzione) rimane costante. Tale principio vale solamente se il sistema di riferimento del corpo è
fermo o dotato di moto rettilineo uniforme. Tale sistema X Y Z si chiama inerziale. La Terra, avendo
il moto rotatorio intorno all’asse polare, è un sistema (x y z) non inerziale. Descrive un giro (360°, 2π)
in 24 ore sideree; a cui corrispondono 900' in un’ora siderea e 902,5' in un’ora media, anche se per
brevità diremo che la velocità angolare ρ è: 900'/h. Un osservatore al polo nord (e in generale in φ
nord), osservando il moto apparente degli astri -orario- deduce che la Terra sta girando in senso
antiorario; per l’osservatore al polo Sud la Terra gira in senso orario. La velocità periferica oraria di
un punto della Terra è vφ = 900'⋅cosφ/h (sull’ellissoide 1' è ∼ 1 miglio); decresce con continuità
dall’equatore ai poli: in φ 0° vφ = 900'; in φ 45° vφ 636'; in φ 90° vφ 0'. Diamo ora un cenno di
spiegazione elementare al fenomeno della “forza” composta di Coriolis; ma lo studio esaustivo è nella
Meccanica ed in Matematica superiore.
Ci esprimiamo con un’astrattezza (pertanto chiediamo al lettore uno sforzo d’immaginazione): un
primo osservatore, quello nel “sistema inerziale”, è lontano dalla Terra; un secondo osservatore è
dalle parti del polo: Polo Nord (o Polo Sud), è nel sistema “non inerziale”. Per il polo transita un
SCARROCCIO E DERIVA
173
corpo dotato di moto rettilineo uniforme; è diretto verso la Norvegia Settentrionale (o verso Capo
Horn), proprio in direzione della stella Alnilam, ad esempio (Alnilam è stella “equatoriale”).
L’osservatore “inerziale” constata, nel tempo, che la velocità vettoriale non cambia: la traiettoria del
corpo è sempre parallela all’asse X del sistema ad esempio, verso Alnilam. Non pensa allo stesso
modo il II osservatore, al polo. Egli, che mantiene lo sguardo verso la Norvegia, nota che la traiettoria
del corpo sta deviando verso la Groenlandia; pensa che una forza lo sposti verso destra (o in Oceano
Pacifico Meridionale, verso sinistra per l’osservatore al polo sud). Ma quando l’osservatore del Polo
gira lo sguardo verso Alnilam, nota che il corpo procede sempre verso la stella, verso lo stesso punto
dello spazio. Riconosce che ha ragione l’osservatore “inerziale“. Ecco perché la forza di Coriolis è
apparente (“fittizia” dice il Prof. Stenner che nel suo libro di Meteorologia spiega con chiarezza
l’ortogonalità della “forza” rispetto alla traiettoria).
Quando con queste parole, più o meno, spiegavo tale fenomeno ai miei allievi, notavo che
l’interesse di qualche studente volgeva verso una verifica: “ma se il corpo parte dall’equatore
andando verso Nord o verso Sud? Non mi trovo, Prof.!” “Non dimenticare la premessa: astrattezza ed
elementarità”. Sia chiaro che il polo è un punto speciale per l’osservazione, un punto fisso dello
spazio (escludiamo, per semplicità, il moto di rivoluzione). “Comunque un ulteriore passo elementare
si può fare; proviamoci”.
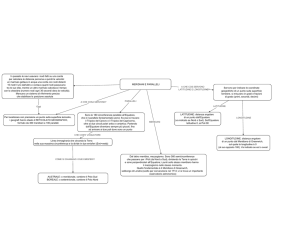
Una nave parte dall’equatore con rotta Nord o Sud e con velocità v (oppure una massa d’aria dal
limite della troposfera equatoriale segue il gradiente barico, verso Nord o verso Sud). Si segua la
figura 12. Abbiamo già detto della diminuzione della velocità periferica dei punti della Terra
dall’equatore ai poli. La nave, avanzando di φ in φ', tende per inerzia a conservare la precedente
velocità, quella -maggiore- del punto terrestre precedente. Da qui il trascinamento verso Est: a destra
in φ Nord a sinistra in φ Sud rispetto alla traiettoria meridiana iniziale.
Analoghe considerazioni spiegano gli altri movimenti abbozzati nella figura 12 e riguardanti corpi
che si muovono inizialmente lungo un arco di parallelo φ. Nei corpi che seguono, in entrambi gli
emisferi, una traiettoria verso oriente si verifica la somma della velocità v con vφ, e volgono verso φ
minori; in quelli che seguono una traiettoria verso occidente si verifica la differenza tra vφ e v, e
volgono verso φ maggiori; entrambi deviano alla ricerca di equilibri ... (regimi, si dice nei venti, che
non saranno proprio uguali nei due casi, verso levante e verso ponente, specialmente se i venti sono
forti). È stata soltanto delineata una traccia di un problema interessante a cui lo studio della
Meteorologia, con ulteriori considerazioni e approfondimenti, dà risposte esaurienti.
Fig 12. Rotazione della terra e forza
apparente; deviante: verso destra in φN ,
verso sinistra in φS.