TENSIONI ALTERNATE SINUSOIDALI
Una tensione o una corrente si dice sinusoidale quando la sua ampiezza al variare del
tempo è proporzionale ad una funzione matematica detta seno. Il seno è una funzione
disponibile sulle calcolatrici scientifiche. Ricordiamo che la tensione disponibile negli
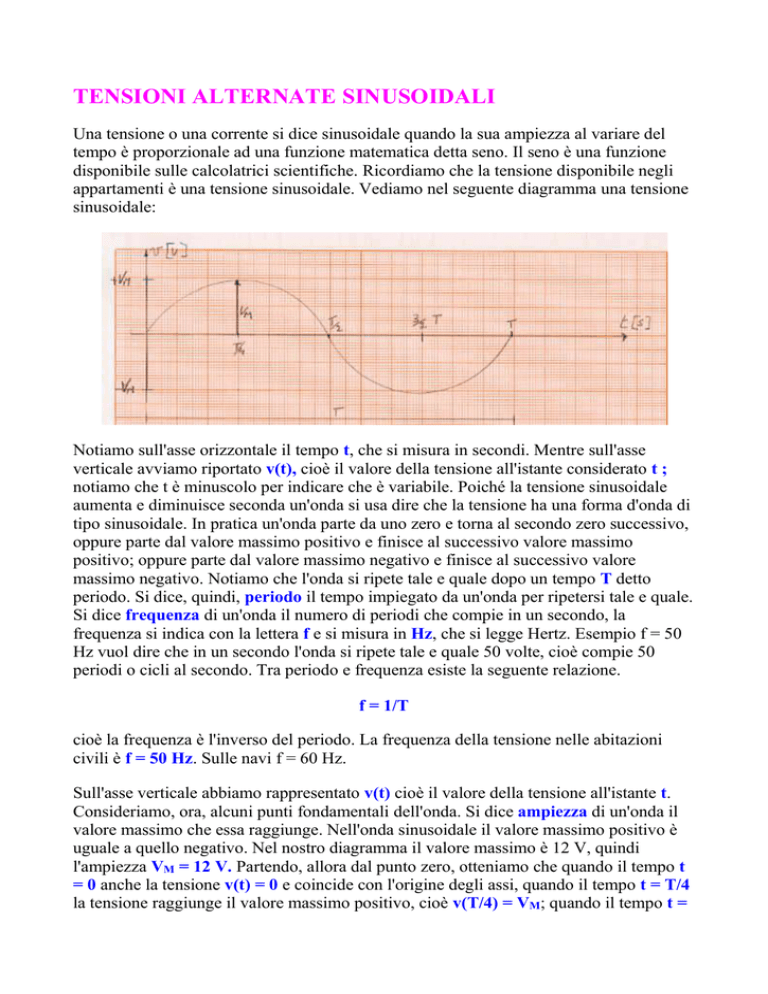
appartamenti è una tensione sinusoidale. Vediamo nel seguente diagramma una tensione
sinusoidale:
Notiamo sull'asse orizzontale il tempo t, che si misura in secondi. Mentre sull'asse
verticale avviamo riportato v(t), cioè il valore della tensione all'istante considerato t ;
notiamo che t è minuscolo per indicare che è variabile. Poiché la tensione sinusoidale
aumenta e diminuisce seconda un'onda si usa dire che la tensione ha una forma d'onda di
tipo sinusoidale. In pratica un'onda parte da uno zero e torna al secondo zero successivo,
oppure parte dal valore massimo positivo e finisce al successivo valore massimo
positivo; oppure parte dal valore massimo negativo e finisce al successivo valore
massimo negativo. Notiamo che l'onda si ripete tale e quale dopo un tempo T detto
periodo. Si dice, quindi, periodo il tempo impiegato da un'onda per ripetersi tale e quale.
Si dice frequenza di un'onda il numero di periodi che compie in un secondo, la
frequenza si indica con la lettera f e si misura in Hz, che si legge Hertz. Esempio f = 50
Hz vuol dire che in un secondo l'onda si ripete tale e quale 50 volte, cioè compie 50
periodi o cicli al secondo. Tra periodo e frequenza esiste la seguente relazione.
f = 1/T
cioè la frequenza è l'inverso del periodo. La frequenza della tensione nelle abitazioni
civili è f = 50 Hz. Sulle navi f = 60 Hz.
Sull'asse verticale abbiamo rappresentato v(t) cioè il valore della tensione all'istante t.
Consideriamo, ora, alcuni punti fondamentali dell'onda. Si dice ampiezza di un'onda il
valore massimo che essa raggiunge. Nell'onda sinusoidale il valore massimo positivo è
uguale a quello negativo. Nel nostro diagramma il valore massimo è 12 V, quindi
l'ampiezza VM = 12 V. Partendo, allora dal punto zero, otteniamo che quando il tempo t
= 0 anche la tensione v(t) = 0 e coincide con l'origine degli assi, quando il tempo t = T/4
la tensione raggiunge il valore massimo positivo, cioè v(T/4) = VM; quando il tempo t =
T/2 la tensione ritorna a zero, cioè v(T/2) = 0; quando il tempo t è uguale a 3T/2 la
tensione raggiunge il valore massimo negativo, cioè v(3T/2)= - VM; infine, quando il
tempo t è uguale ad un periodo la tensione ritorna a zero, cioè v(T) = 0.
Si dice valore efficace di un'onda sinusoidale il valore equivalente che produce gli stessi
effetti di riscaldamento della tensione continua. Dato cioè un resistore di valore R, se per
esempio lo alimentiamo con tensione continua E = 12 V, oppure lo alimentiamo con
tensione alternata avente valore efficace V = 12 V gli effetti sul riscaldamento del
resistore sono equivalenti. Il valore efficace di una tensione sinusoidale lo indichiamo
con la lettera V maiuscola. Il valore efficace della tensione si misura in Volt.
Conoscendo il valore massimo di una tensione sinusoidale, possiamo calcolare il valore
efficace con la seguente formula
V = VM / 2 = 0,707 VM
Lo stesso discorso fatto per la tensione sinusoidale vale anche per la corrente
sinusoidale, infatti un circuito alimentato con tensione sinusoidale dà luogo ad una
corrente sinusoidale. Il diagramma è il seguente:
Indichiamo con IM l'ampiezza della corrente; il valore del periodo e della frequenza
restano gli stessi, cioè tensione e corrente hanno lo stesso periodo, la stessa frequenza, e
la stessa forma d'onda. Per calcolare il valore efficace della corrente I usiamo la seguente
formula:
I = IM / 2 = 0,707 IM
E' opportuno, ora, riepilogare la simbologia.
La lettera V maiuscola da sola indica o una tensione continua o il valore efficace di una
tensione alternata; la lettera V maiuscola vicino ad un numero rappresenta il Volt, cioè
l'unità di misura della tensione; esempio:
V = 220 V
si legge che esiste una tensione V che può essere o continua pari a 220 V oppure
alternata con valore efficace 220 V.
La lettera v minuscola indica una tensione che varia nel tempo.
La lettera I maiuscola da sola indica o una corrente continua o il valore efficace di una
corrente alternata;
I = 10 A
si legge che esiste una corrente I che può essere o continua pari a 10 A oppure alternata
con valore efficace 10 A.
La lettera i minuscola indica una corrente che varia nel tempo.
VETTORI ROTANTI
Un modo di rappresentare graficamente le grandezze sinusoidali è quello dei vettori
rotanti. Si prende come riferimento un asse orizzontale ed un punto fermo O, scelti a
piacere, come nel seguente schema:
si disegna in una scala a piacere un segmento che parte dal punto 0 e lungo quanto
l'ampiezza della tensione da rappresentare. Nel nostro caso, volendo rappresentare una
tensione avente valore efficace V= 220 V, ci calcoliamo il valore massimo VM = 220 2
= 311 V, e disegniamo un segmento di lunghezza pari a 3,11 cm essendo la scala scelta 1
cm = 100 V; mettiamo sul segmento una direzione verso l'esterno mediante una freccia;
in pratica abbiamo ottenuto un particolare vettore che ha modulo pari a VM , direzione e
verso indicati dalla freccia. Tale vettore però non è fisso ma ruota in senso antiorario
attorno al punto 0 con velocità angolare . Per calcolare usiamo la formula
=2f
cioè la velocità angolare è uguale a 2 moltiplicato per 3,14 per la frequenza f. si
misura in radianti al secondo. è detta anche pulsazione. Consideriamo ora la
proiezione del segmento 0P sull'asse orizzontale, tale proiezione che è pari al segmento
OX, rappresenta istante per istante la tensione v avente valore massimo VM e frequenza
f.
Naturalmente anche una corrente alternata sinusoidale si può rappresentare col metodo
dei vettori rotanti.
CIRCUITO PURAMENTE RESISTIVO
Un circuito si dice puramente resistivo quando compaiono solo resistenze. Lo schema
elettrico è il seguente:
Nel circuito puramente resistivo la corrente è in fase con la tensione. La legge di Ohm
diventa:
V=RI
Dove V e I sono vettori; mentre R la consideriamo costante. Usando i vettori rotanti
otteniamo che il vettore corrente è parallelo al vettore tensione, in quanto tensione e
corrente sono in fase.
CIRCUITO PURAMENTE INDUTTIVO
Un circuito si dice puramente induttivo quando compaiono solo delle induttanze. Lo
schema elettrico è il seguente:
Nella induttanza L, essendo sottoposta a corrente alternata vi si genera una forza
elettromotrice indotta e, secondo la legge di Farady, Neumann, Lenz, tale forza
elettromotrice è uguale e opposta alla tensione che l'ha generata, cioè v = - e.
Si dice reattanza induttiva l'ostacolo che la induttanza L oppone al passaggio della
corrente alternata. La reattanza induttiva si indica con la lettera XL, si misura in , si
calcola con la seguente formula:
XL = L
Tale formula ci dice che la reattanza della bobina avente induttanza L è pari al prodotto
della pulsazione per l'induttanza L della bobina. Dove = 2 f.
Tra tensione e corrente nel condensatore esiste uno sfasamento di 90° , pari a /2, con la
tensione che è in anticipo rispetto alla corrente. La legge di Ohm diventa:
V = j XL I
Dove V ed I sono vettori, mentre XC si considera costante se la frequenza è costante. j è
un operatore matematico che applicato alla corrente la sfasa di 90° in anticipo, quindi V
che si ottiene moltiplicando la corrente per j è in anticipo di 90° rispetto alla corrente.
CIRCUITO PURAMENTE CAPACITIVO
Un circuito si dice puramente capacitivo quando sono presenti solo condensatori. Lo
schema elettrico è il seguente:
In pratica il condensatore è costretto a caricarsi, scaricarsi e caricarsi di segno opposto
seguendo la tensione alternata applicata ai suoi capi. Si dice reattanza capacitiva
l'ostacolo che il condensatore oppone al passaggio della corrente alternata. La reattanza
capacitiva si indica col simbolo XC, si misura in , si calcola con la seguente formula:
XC = 1/ C
Tale formula ci dice che la reattanza del condensatore avente capacità C è pari
all'inverso del prodotto della pulsazione per la capacità C del condensatore. Dove =
2 f.
Tra tensione e corrente nel condensatore esiste uno sfasamento di 90° , pari a /2, con la
corrente che va in anticipo rispetto alla tensione. La legge di Ohm diventa:
V = - j XC I
Dove V ed I sono vettori, mentre XC si considera costante se la frequenza è costante. j è
un operatore che applicato alla corrente la sfasa di 90° in anticipo, poiché però compare
il segno - la sfasa in ritardo di 90°, di conseguenza la tensione è in ritardo di 90° rispetto
alla corrente.
CIRCUITO RL
Si dice circuito RL un circuito in cui compaiono solo resistenze e induttanze. Lo schema
elettrico è il seguente:
Nel circuito RL si combinano i due effetti della resistenza del resistore R e della
reattanza della bobina L, per cui si ha uno sfasamento complessivo tra tensione e
corrente, che dipende sia da R che da XL. Si dice impedenza del circuito RL l'ostacolo
che esso oppone al passaggio della corrente alternata. L'impedenza si indica con la
lettera Z, si misura in si calcola con la seguente formula:
Z = R2 + ( L)2
Z è un vettore il cui modulo lo indichiamo con Z. Tale formula ci dice che il modulo
dell'impedenza Z si calcola facendo la radice quadrata della somma di R al quadrato +
( L) tutto al quadrato, che poi è la reattanza al quadrato. Invece Z vettore è : Z = R +
j L. La legge di Ohm diventa:
V = Z I = (R + j L) I
Cioè la tensione vettore ai capi di un circuito RL è uguale al prodotto della impedenza Z
vettore per la corrente vettore.
Per disegnare i vettori usiamo il seguente schema:
cioè prima disegniamo la tensione ai capi di R che è orizzontale e quindi VR = RI; poi
disegniamo la tensione ai capi della induttanza L, che è sfasata di 90° in anticipo quindi
VL = j XL I, poi facciamo la somma vettoriale dei due vettori e otteniamo il vettore V,
che è la tensione applicata al circuito RL. Per calcolare lo sfasamento cioè l'angolo
tra tensione V e corrente I si può usare la seguente formula:
= arctg L/R
cioè arcotangente del rapporto tra parte immaginaria e parte reale.
CIRCUITO RC
Si dice circuito RC un circuito in cui compaiono solo resistenze e condensatori. Lo
schema elettrico è il seguente:
Nel circuito RC si combinano i due effetti della resistenza del resistore R e della
reattanza del condensatore C, per cui si ha uno sfasamento complessivo tra tensione e
corrente, che dipende sia da R che da XC. Si dice impedenza del circuito RC l'ostacolo
che esso oppone al passaggio della corrente alternata. L'impedenza si indica con la
lettera Z, si misura in si calcola con la seguente formula:
Z = R2 + (1/ C)2
Z è un vettore il cui modulo lo indichiamo con Z. Tale formula ci dice che il modulo
dell'impedenza Z si calcola facendo la radice quadrata della somma di R al quadrato +
(1/ C) tutto al quadrato, che poi è la reattanza al quadrato. Invece Z vettore è : Z = R - j
(1/C). La legge di Ohm diventa:
V = Z I = (R - j (1/ C) I
Cioè la tensione vettore ai capi di un circuito RC è uguale al prodotto della impedenza Z
vettore per la corrente vettore.
Per disegnare i vettori usiamo il seguente schema:
cioè prima disegniamo la tensione ai capi di R che è orizzontale e quindi VR = RI; poi
disegniamo la tensione ai capi del condensatore C, che è sfasata di 90° in ritardo VC = - j
XC I, poi facciamo la somma vettoriale dei due vettori e otteniamo il vettore V, che è la
tensione applicata al circuito RC. Per calcolare lo sfasamento cioè l'angolo tra
tensione V e corrente I si può usare la seguente formula:
= arctg - 1 / RC
cioè arcotangente del rapporto tra parte immaginaria e parte reale.
CIRCUITO RLC
Si dice circuito RLC un circuito in cui compaiono resistenze, induttanze e condensatori.
Lo schema elettrico è il seguente:
Nel circuito RLC si combinano gli effetti della resistenza del resistore R, della reattanza
della bobina L e della reattanza del condensatore C, per cui si ha uno sfasamento
complessivo tra tensione e corrente, che dipende sia da R sia da XL sia da XC. Si dice
impedenza del circuito RLC l'ostacolo che esso oppone al passaggio della corrente
alternata. L'impedenza si indica con la lettera Z, si misura in si calcola con la
seguente formula:
Z = R2 + ( L - 1/ C)2
Z è un vettore il cui modulo lo indichiamo con Z. Tale formula ci dice che il modulo
dell'impedenza Z si calcola facendo la radice quadrata della somma di R al quadrato +
( L - 1/ C) tutto al quadrato, che poi è la reattanza al quadrato. Invece Z vettore è : Z
= R + j ( L - 1/C). La legge di Ohm diventa:
V = Z I = (R + j ( L - 1/ C) I
Cioè la tensione vettore ai capi di un circuito RLC è uguale al prodotto della impedenza
Z vettore per la corrente vettore.
Per disegnare i vettori usiamo il seguente schema:
cioè prima disegniamo la tensione ai capi di R che è orizzontale e quindi VR = RI; poi
disegniamo la tensione ai capi della induttanza L, che è sfasata di 90° in anticipo quindi
VL = j XL I; poi disegniamo la tensione ai capi del condensatore C, che è sfasata di 90°
in ritardo VC = - j XC I, poi facciamo la somma vettoriale dei tre vettori e otteniamo il
vettore V, che è la tensione applicata al circuito RLC. Per calcolare lo sfasamento
cioè l'angolo tra tensione V e corrente I si può usare la seguente formula:
= arctg ( L - 1/ C) / R
cioè arcotangente del rapporto tra parte immaginaria e parte reale.
Dal sito
http://www.scuolaelettrica.it/superiore/tecnologico/informatico/elettronica.htm












