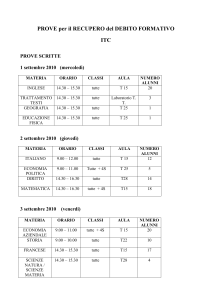
Misura della carica elementare
permezzodello shotnoise
EdoardoMilotti
Corso diMetodi diTrattamento delSegnale
A.A.2015-16
Formule perloshotnoise
h|I(f )|2 i = 2eI0
Integrazione sulla banda difrequenza B,
assumendo unvero rumore bianco
hI 2 i = h|I(f )|2 iB = 2eI0 B
hV 2 i = R2 h|I(f )|2 iB = 2eI0 BR2
Calcolando lafluttuazione totale è dunque possibile trovare il valore della carica
elementare:
hV 2 i
e=
2I0 BR2
Shot‐noise measurements of the electron charge: An undergraduate experi
D. R. Spiegel and R. J. Helmer
Citation: American Journal of Physics 63, 554 (1995); doi: 10.1119/1.17867
View online: http://dx.doi.org/10.1119/1.17867
View Table of Contents: http://scitation.aip.org/content/aapt/journal/ajp/63/6?ver=pdfcov
Published by the American Association of Physics Teachers
Noi usiamo unfotodiodo
semiconduttore alposto
della fotocellula
Alimentazione
fotocellula
Questaresistenza nonc’è nel nostro schema:sepresente il circuito
auto-oscilla acausa dell’alta capacità ditransizione delfotodiodo
Nel circuito mostrato laresistenza da150kche va amassa dall’input
non-invertente è stata inserita perminimizzare il contributo del
rumore incorrente dell’OP-AMP,tenendo conto diun’impedenza
“infinita”della fotocellula.Questaipotesi non è valida sec’è un
fotodiodo.
55-23
r
5655-20
Order Number LF411ACH
DS005655-21
OP-AMPLF411
or LF411MH/883 (Note 1)
See NS Package Number H08A
Undistorted Output
VoltageDual-In-Line
Swing
Package
DS005655-22
Open Loop Frequency
Response
DS005655-7
Top View
Order Number LF411ACN,
LF411CN or LF411MJ/883 (Note 1)
See NS Package Number N08E or J08A
DS005655-24
DS005655-25
Lascelta dell’LF411 nonè ottimale.Hauna risposta infrequenza piuttosto scarsa,ehail problema diunoffset
(posizione dello zerodella tensione inuscita)che non è piccolo.
www.national.com
Open Loop Frequency
Response
Nella regione abassa
frequenza (f<10kHz)c’è
una significativa
diminuzione delguadagno
S005655-24
DS005655-25
Ilfiltro passa-banda (un filtro passa altoincascata conunfiltro passa-basso)limita la
regione utileadunintervallo bendefinito
Laconversione aRMSviene realizzata dalcircuito integrato AD637JQ
FEATURES
High accuracy
0.02% maximum nonlinearity, 0 V to 2 V rms input
0.1% additional error to crest factor of 3
Wide bandwidth
8 MHz at 2 V rms input
600 kHz at 100 mV rms
Computes
True rms
Square
Mean square
Absolute value
dB output (60 dB range)
Chip select/power-down feature allows
Analog three-state operation
Quiescent current reduction from 2.2 mA to 350 µA
FUNCTIONAL BLOCK DIAGRAM
BUFF IN
+
BUFF OUT
–
25kΩ
VIN
SQUARER/
DIVIDER
ABSOLUTE
VALUE
RMS OUT
–
+
DEN
INPUT
25kΩ
–
CAV
+
OUTPUT
OFFSET
dB OUTPUT
BIAS
COMMON
CS
00788-001
Data Sheet
High Precision, Wideband
RMS-to-DC Converter
AD637
Figure 1.
GENERAL DESCRIPTION
The AD637 is a complete, high accuracy, rms-to-dc converter
that computes the true rms value of any complex waveform. It
offers performance that is unprecedented in integrated circuit
rms-to-dc converters and comparable to discrete and modular
techniques in accuracy, bandwidth, and dynamic range. The
AD637 computes the true root mean square, mean square, or
absolute value of any complex ac (or ac plus dc) input waveform
and gives an equivalent dc output voltage. The true rms value of
a waveform is more useful than an average rectified signal
because it relates directly to the power of the signal. The rms
facilitates the addition of precision rms measurement to remote
or handheld applications where minimum power consumption
is critical. In addition, when the AD637 is powered down, the
output goes to a high impedance state. This allows several
AD637s to be tied together to form a wideband true rms
multiplexer.
The input circuitry of the AD637 is protected from overload
voltages in excess of the supply levels. The inputs are not
damaged by input signals if the supply voltages are lost.
C1
10µF
25V
+
+
–VS
+VS
FILTER
BUF_IN
4
1
2
OUT
5
3
6
1
C2
10µF
25V
IN
BUFF OUT
BUFF IN
16
BUF_OUT
2
3
+VS
R1
1M
R2
50k
+VS
4
R3
4.7k
5
–VS
6
7
NIC
Z1
AD637
COMMON
NIC
OUTPUT
OFFSET
+VS
CS
–VS
DEN INPUT
CAV
NIC
NIC
R4
24.3k
15
14
CIN
22µF
16V
RMS_IN
13
C3
0.1µF
12
C4
0.1µF
11
+
10
+VS
–VS
DC_OUT
DC_OUT
CAV
22µF
16V
9
R5
24.3k
+
CF1
47µF
25V
CF2
47µF
25V
00788-130
+
RMS OUT
dB OUTPUT
DB_OUT
8
VIN
+
RMS_IN
NIC = NO INTERNAL CONNECTION
Figure 30. Evaluation Board Schematic
AC OR DC INPUT SIGNAL SOURCE
Acausa delguadagno variabile infunzione della frequenza, si deve modificare la
formula perlacarica elementare
I = I0 +
Z
I(f )e2⇡if t dt
• Trasformata diFourier della corrente
f >0
V 0 = R0 I 0
• Amplificazione DCintransimpedenza del
sistema (R0guadagno delprimo stadio)
V (f ) = R0 I(f )
• Amplificazione intransimpedenza delle
componenti diFourier
h|V (f )|2 i = 2eI0 R02
2
VRMS
=
=
Z
ZB
B
h|V (f )|2 idf
• Shotnoise intensione
• Tensione RMSrilevata inuscita
2eI0 R02 df = 2eI0 R02 B
Introduciamo ora unfattore che tiene conto sia delguadagno variabile infrequenza
delprimo stadio che delguadagno variabile infrequenza ditutti gli stadi successivi
V0 = VDC OUT
VRMS (f ) = g(f )Vtest (f )
2
VRMS
=
=
Z
ZB
B
hg 2 (f )|V (f )|2 idf
2eI0 R02 g 2 (f )df = 2eV0 R0
Z
g 2 (f )df
B
Lamisura richiede duepassaggi
1. Misura dig(f),utilizzando ungeneratore difunzioni nel testinput
2. Misura dello shotnoise
2
2
VRMS
= hVamp
i + 2eV0 R0
2
e =pendenza della retta nel piano(V0 , VRMS )
Z
g 2 (f )df
B