ESAME DI FISICA GENERALE - CHIMICA INDUSTRIALE E CHIMICA APPLICATA E
AMBIENTALE
18 LUGLIO 2011
IMPORTANTE: Risolvere a scelta un esercizio tra M1 e M2, uno tra EM1 e EM2 e uno tra O1 e T1. NON
SVOLGERE esercizi dello stesso gruppo. Ogni esercizio vale 10 punti.
M1
Un corpo di massa m si muove con velocità di modulo v0 su un piano orizzontale privo di attrito, in fondo al quale
si trova una molla di costante elastica k.
M1.a. Calcolare la massima compressione della molla.
[3 punti]
M1.b. Dopo che la molla si riespande, il corpo viene lanciato indietro con velocità di modulo vf . Calcolare vf in
funzione di v0 .
[3 punti]
Si supponga adesso che il piano sia ruvido, con coefficiente di attrito dinamico µd , e abbia lunghezza L.
M1.c. Calcolare la massima compressione in questo caso.
[2 punti]
M1.c. Calcolare, in questo caso, la velocità vf . Di quanto si è ridotta rispetto al caso calcolato al punto (b)?
[2 punti]
M2
Una cassa di massa m è posta sul pianale di un camion. Sia µs il coefficiente di attrito statico tra cassa e pianale.
Il camion si muove con accelerazione a0 . Si supponga che la cassa non scivoli sul pianale.
M2.a. Tracciare il diagramma delle forze che agiscono su m, con particolare attenzione alla direzione delle forze.
[3 punti]
M2.b. Calcolare la forza di attrito che agisce sulla cassa.
[4 punti]
M2.c. Calcolare il massimo valore di a0 in modo che la cassa non scivoli.
[3 punti]
R
D
V0
C
x
T
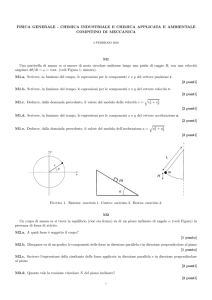
Figura 1. Sinistra: esercizio EM1. Centro: esercizio EM2. Destra: esercizio T1.
EM1
Nella zona di spazio ombreggiata in Figura (sinistra) è presente un campo magnetico entrante nel piano del foglio,
di modulo B. Si consideri il circuito conduttore, di resistenza R e di lato D, indicato in Figura. Un agente esterno
spinge il circuito all’interno della zona in cui è presente il campo magnetico a velocità costante v = dx/dt > 0.
EM1.a. Calcolare il flusso del campo magnetico attraverso la spira, e la sua derivata temporale in funzione di v.
[3 punti]
1
EM1.b. La corrente indotta nella spira fluisce in senso orario o antiorario? Perchè?
[2 punti]
EM1.c. Calcolare il valore della fem indotta sulla spira e la corrente indotta in essa, in funzione di v.
[3 punti]
EM1.d. Calcolare la potenza dissipata dalla resistenza, in funzione della velocità v.
[2 punti]
EM2
Si consideri il circuito RC in Figura (centro), ove V0 è la fem del generatore. All’istante t = 0 il circuito viene
chiuso. Ad un istante t generico sia I la corrente nel circuito e Q la carica nel condensatore. Si consideri il breve
intervallo di tempo dt, nel quale il generatore fornisce al circuito una carica dQ = Idt.
EM2.a. Dare l’espressione per l’energia dEV erogata dal generatore nell’intervallo di tempo dt.
[3 punti]
EM2.b. Dare l’espressione per l’energia dER dissipata dalla resistenza nell’intervallo di tempo dt.
[3 punti]
EM2.c. Dare l’espressione per l’energia dEC che viene accumulata nel condensatore nell’intervallo di tempo dt.
[2 punti]
EM2.d. Usando il principio della conservazione della energia, si ottenga l’equazione del circuito.
[2 punti]
O1
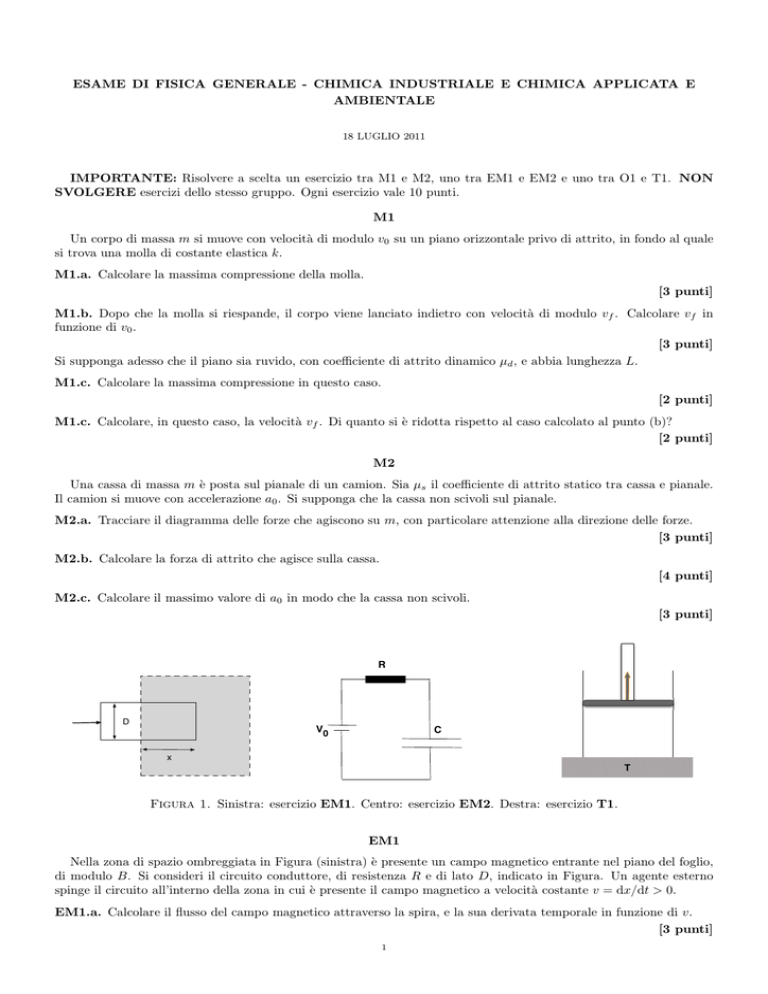
Sul fondo di un canale pieno d’acqua si trova una lampadina accesa. Si considerino due raggi luminosi emessi dalla
lampadina, il primo sia perpendicolare alla superficie dell’acqua mentre il secondo abbia un angolo di incidenza θ1 ≪ 1.
O1.a. Disegnare il percorso dei due raggi originari e dei raggi rifratti nell’atmosfera.
[2 punti]
O1.b. Individuare nel disegno la posizione dell’immagine della lampadina. Si tratta di una immagine reale o virtuale?
[3 punti]
O1.c. Osservato da fuori dall’acqua, il canale appare avere una profondità D. Se n è l’indice di rifrazione dell’acqua
relativo all’aria, quanto è profondo il canale in realtà?
[3 punti]
O1.d. Rispondere al quesito (c) nel caso in cui D = 2 m e n = 1.3.
[2 punti]
T1
Un numero n di moli di gas perfetto si trovano in un recipiente di volume iniziale V1 , chiuso da un pistone mobile, e
mantenuto a temperatura costante T da un bagno di calore (vedi Figura, destra). Il pistone viene sollevato lentamente
in modo che il gas occupi un volume finale V2 > V1 .
T1.a. Di quanto è variata l’energia interna del gas durante la trasformazione?
[3 punti]
T1.b. Calcolare il calore assorbito e il lavoro compiuto dal gas.
[3 punti]
T1.c. È possibile calcolare la variazione di entropia in questa trasformazione usando la formula
Z
dQ
∆S =
?
T
[2 punti]
T1.d. Calcolare la variazione di entropia tra lo stato iniziale e finale.
[2 punti]