Foglio esercizi n. 9 del 1.12.2012

1/3
Foglio esercizi n. 9 del 1.12.2012
Esercizio 9.1
Per il comparatore rappresentato in figura:
1. determinare l’andamento
ingresso-uscita;
della
caratteristica
2. determinare il valore (e il segno) delle correnti in
RL , R1 , R2 e nei diodi, per tensione in ingresso a)
VS = 5 V e b) VS = 10 V;
R2
VS
R1
RL
VR
3. determinare il valore (e il segno) delle correnti in
RL , R1 , R2 e nei diodi, quando la tensione in ingresso viene portata al valore VS = 0, direttamente
dal valore indicato al punto precedente;
VU
1
2
4. determinare il valore (e il segno) delle correnti in RL , R1 , R2 e nei diodi, per tensione in
ingresso a) VS = −5 V e b) VS = −10 V;
5. determinare il valore (e il segno) delle correnti in RL , R1 , R2 e nei diodi, quando la tensione
in ingresso viene portata al valore VS = 0, direttamente dal valore indicato al punto
precedente.
R1 = 1 kΩ, R2 = 4 kΩ, VO+ = −VO− = 12 V, VR = 0.5 V, VZ = 4.3 V, Vγ = 0.7 V, RL = 270 Ω
(VO+ e VO− rappresentano i valori di saturazione dell’uscita dell’A.O.).
Esercizio 9.2
Per il comparatore rappresentato in figura (v.esercizio precedente):
1. determinare l’andamento della caratteristica ingresso-uscita;
2. determinare l’andamento della tensione d’uscita (a regime) se la tensione d’ingresso vs
è una tensione a onda triangolare simmetrica a valor medio nullo e con valore di picco
VM = 10 V;
3. detti t1 e t2 , rispettivamente, gli istanti in cui l’uscita commuta verso l’alto e verso il
basso, calcolare il valore della corrente attraverso la resistenza RL e attraverso i diodi
+ −
+
negli istanti t−
1 , t1 , t2 e t2 ;
4. calcolare la potenza dissipata nella resistenza RL e in ciascuno dei diodi negli istanti
indicati.
R1 = 10 kΩ, R2 = 10 kΩ, VR = 1.5 V, RL = 330 Ω, Vγ = 0.7 V, VZ = 5.2 V, VO+ = −VO− = 12 V]
(VO+ e VO− rappresentano i valori di saturazione dell’uscita dell’A.O.).
2/3
Esercizio 9.3
V+
1. Utilizzando il teorema di scomposizione (e il taglio indicato
a lezione per il calcolo della resistenza d’uscita di un amplificatore a doppio carico) determinare la resistenza d’uscita Ro
del demagnificatore rappresentato in figura;
Ro
R
1
2. ripetere il calcolo senza utilizzare il t.s.
2
RE
[R = 3 kΩ, RE = 1.5 kΩ;
Q: hf e1 = hf e2 = 210, hie1 = hie2 = 2 kΩ, hoe1 = hoe2 = (25 kΩ)−1 ]
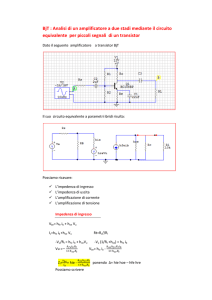
Esercizio 9.4
V+
RE
Utilizzando il teorema di scomposizione (e il taglio indicato) determinare la resistenza vista da RC nel circuito
rappresentato in figura.
[RC = 2 kΩ, RE = 1 kΩ, R = 0.5 kΩ;
A.O. con Avol = 105 (costante), Rin = 200 kΩ, R0 = 0;
transistor con hf e = 200, hie = 2 kΩ, hoe = (20 kΩ)−1 .]
+ vin −
Rin
vs
RC
hoe
R
hie
-
Avolo vin
R
ib
H
H
hf e ib
RE
?
∗ Sulla base del valore delle resistenze d’ingresso e d’uscita, a quale amplificatore “ideale” è
assimilabile il sistema?
+
altri esercizi tratti da compiti d’esame su generatori di forme d’onda e comparatori.
3/3
Risultati:
Es. 9.1: 1): VH = 5 V, VL = −5 V, soglie : V1 = 1.875 V, V2 = −0.625 V
2 a): IRL = 25.9 mA, IR1 = IR2 = 0, ID = 25.9 mA
2 b): IRL = 25.9 mA, IR1 = IR2 = 1 mA, ID = 26.9 mA
3): IRL = 25.9 mA, IR1 = IR2 = −1 mA, ID = 24.9 mA
4 a): IRL = −25.9 mA, IR1 = IR2 = 0, ID = −25.9 mA
4 b): IRL = −25.9 mA, IR1 = IR2 = −1 mA, ID = −26.9 mA
5): IRL = −25.9 mA, IR1 = IR2 = 1 mA, ID = −24.9 mA
Es. 9.2: VH = 5.9 V, VL = −5.9 V, soglie : V1 = 8.9 V, V2 = −2.9 V
t = t−
t = t+
1 : P1 = 12.4 mW, P2 = 92.3 mW,
1 : P1 = 96.9 mW, P2 = 13.0 mW
−
t = t2 : P1 = 93.8 mW, P2 = 12.6 mW,
t = t+
2 : P1 = 18.8 mW, P2 = 95.3 mW
Es. 9.3: detta R′ = Rk
"
1
hie2
k
= 9.44 Ω
hoe2 hf e2 + 1
hie1 + R′
1
+ RE k
Yp =
hoe
hf e1 + 1
Yb = 0
βA =
!#−1
= 39.98 × 10−6 Ω−1
hf e
= 0.989 (reaz. positiva di tensione)
R′ + hie
hf e + 1 +
RE
Yo = (Yb + Yp )(1 − βA) = 440.6 × 10−9 Ω−1
Es. 9.4: Yp =
(
Yb = 0
βA =
"
1
R + hie
+ RE kRin k
hoe
(Avol + 1)(hf e + 1)
#)−1
(Rout = 1/Yo = 2.27 MΩ)
= 49.99 × 10−6 Ω−1
hf e
= 0.995 (reaz. positiva di tensione)
R + hie
hf e + 1 +
(Avol + 1)(RE kRin )
Yo = (Yb + Yp )(1 − βA) = 248.8 × 10−9 Ω−1
(Rout = 1/Yo = 4.02 MΩ).