Doppi bipoli

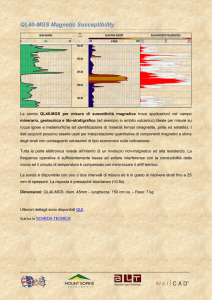
Doppi bipoli
v1
i1
i2
Porta 1
Porta 2
i1
i2
v2
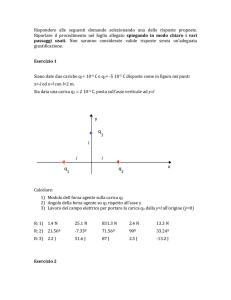
Determinare i parametri Z (R)
r11
r22
{
v 1=r 11 i 1r 12 i 2
v 2=r 21 i 1r 22 i 2
1)
2)
3)
4)
r12 i2
r21 i1
e1
e2
Collegare un generatore di corrente di sonda alla porta 1. Lasciare aperta la porta 2.
Calcolare z11 = v1/i1 e z21 = v2/i1.
Collegare un generatore di corrente di sonda alla porta 2. Lasciare aperta la porta 1.
Calcolare z12 = v1/i2 e z22 = v2/i2.
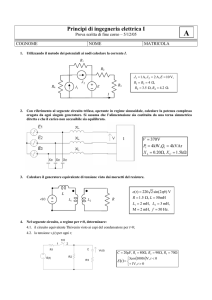
Determinare i parametri Y (G)
i 1= y 11 v 1 y 12 v 2
i
i
g
g
g v
g v
i 2= y 21 v 1 y 22 v 2
1) Collegare un generatore di tensione di sonda alla porta 1. Cortocircuitare la porta 2.
2) Calcolare y11 = i1/v1 e y21 = i2/v1.
3) Collegare un generatore di tensione di sonda alla porta 2. Cortocircuitare la porta 1.
4) Calcolare y12 = i1/v2 e y22 = i2/v2.
{
1
11
2
22
21 1
12 2
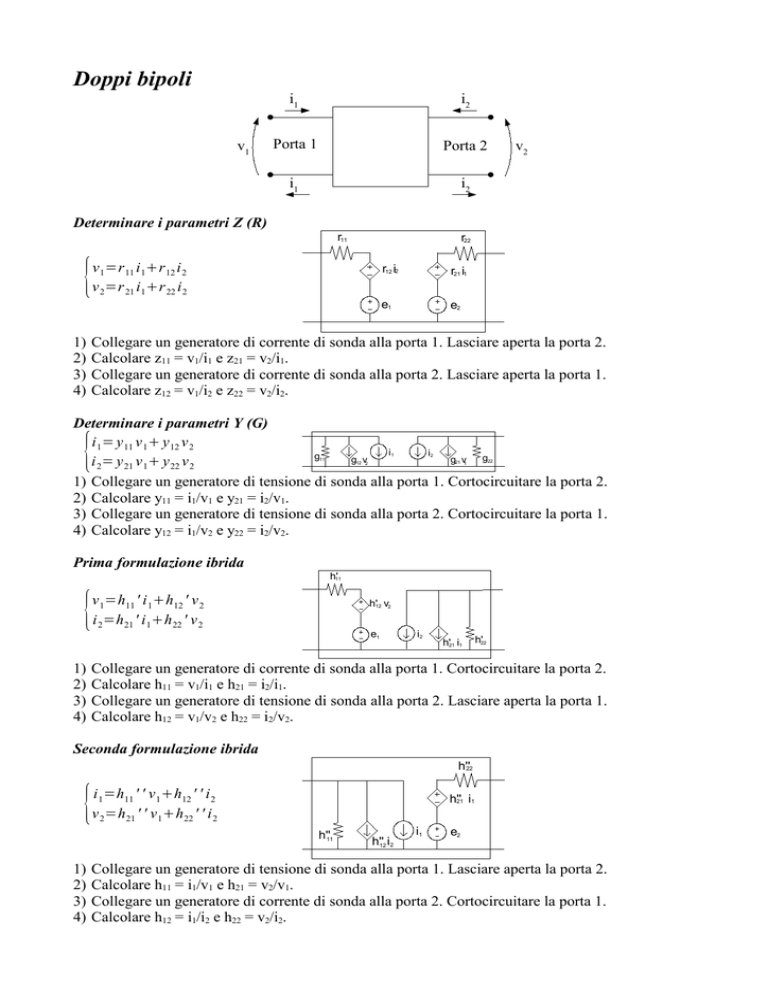
Prima formulazione ibrida
h'11
{
v 1=h11 ' i 1h12 ' v 2
i 2=h 21 ' i 1h 22 ' v 2
1)
2)
3)
4)
h'12 v2
e1
i2
h'21 i1
h'22
Collegare un generatore di corrente di sonda alla porta 1. Cortocircuitare la porta 2.
Calcolare h11 = v1/i1 e h21 = i2/i1.
Collegare un generatore di tensione di sonda alla porta 2. Lasciare aperta la porta 1.
Calcolare h12 = v1/v2 e h22 = i2/v2.
Seconda formulazione ibrida
h''22
{
i 1=h11 ' ' v 1h12 ' ' i 2
v 2=h21 ' ' v 1h 22 ' ' i 2
h''21 i1
h''11
1)
2)
3)
4)
h''12 i2
i1
e2
Collegare un generatore di tensione di sonda alla porta 1. Lasciare aperta la porta 2.
Calcolare h11 = i1/v1 e h21 = v2/v1.
Collegare un generatore di corrente di sonda alla porta 2. Cortocircuitare la porta 1.
Calcolare h12 = i1/i2 e h22 = v2/i2.
Un doppio bipolo si dice reciproco se ha valori uguali sulla diagonale secondaria
r
r
R= 11 m
r m r 22
[
]
Un doppio bipolo reciproco, se ammette la formulazione controllata in corrente, ammette un
circuito equivalente “a T”.
ra
rb
{
r 11=r a r c
r m =r c
r 22 =r b r c
rc
⇔
{
r a =r 11 −r m
r b =r 22 −r m
r c =r m
Analogamente, se la matrice G è reciproca, il doppio bipolo ammette un circuito equivalente “a Π”
gc
ga
gb
Trasformazione Stella -> Triangolo (T -> Π)
r r
R c =r a r b  a b
rc
Trasformazione Triangolo -> Stella (Π -> T)
R a Rb
r c=
R a R bR c
{
g 11=g a g c
g m=−g c
g 22=g b g c
⇔
{
g a =g11g m
g b= g 22g m
g c =−g m