Esercizio 2. Generatore di onda triangolare con duty cycle diverso

Esercizio 2
Progettare un generatore di onda triangolare che abbia:
1.
2.
3.
4.
Uscita variabile tra 0V e 5V;
Frequenza 2kHz;
Tempo di salita pari al doppio di quello di discesa;
Disegnare la carta dei tempi dell’uscita vo e dell’ingresso v+.
Svolgimento
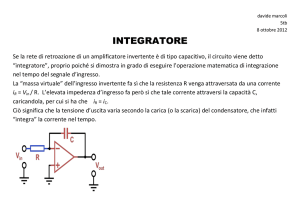
Per realizzare il generatore di onda triangolare utilizziamo un trigger di Schmitt non invertente e
colleghiamo, alla sua uscita un integratore. Lo schema è disegnato in figura:
Figura 1 Il generatore di onde triangolari.
La prima specifica da soddisfare ci dice che l’onda quadra deve variare tra 0V e 5V. Per il circuito
disegnato l’onda triangolare varia tra:
𝑣𝑜𝑚𝑎𝑥 = 𝑉𝑇+
𝑣𝑜𝑚𝑖𝑛 = 𝑉𝑇−
𝑒
Dove:
𝑉𝑇+ è 𝑙𝑎 𝑡𝑒𝑛𝑠𝑖𝑜𝑛𝑒 𝑑𝑖 𝑠𝑜𝑔𝑙𝑖𝑎 𝑠𝑢𝑝𝑒𝑟𝑖𝑜𝑟𝑒 𝑒 𝑉𝑇− è 𝑙𝑎 𝑡𝑒𝑛𝑠𝑖𝑜𝑛𝑒 𝑑𝑖 𝑠𝑜𝑔𝑙𝑖𝑎 𝑖𝑛𝑓𝑒𝑟𝑖𝑜𝑟𝑒 𝑑𝑒𝑙 𝑡𝑟𝑖𝑔𝑔𝑒𝑟
Alimentiamo l’amplificatore operazionale con ±12𝑉 e determiniamo i valori delle resistenze R1 ed
R2 in modo da ottenere un’onda triangolare che varia tra -2.5V e +2.5V. Penseremo
successivamente a traslarla. Sappiamo che per un trigger di Schmitt non invertente si hanno le
relazioni:
𝑉𝑇+ =
𝑅1
𝑉
𝑅2 𝑆𝐴𝑇
𝑉𝑇− =
𝑅1
(−𝑉𝑆𝐴𝑇 )
𝑅2
Sostituendo i valori numerici:
2.5 =
𝑅1
12
𝑅2
→
𝑅2 12
=
= 4.8
𝑅1 2.5
Possiamo scegliere:
𝑅1 = 10𝑘Ω
𝑅2 = 48𝑘Ω
1
→
𝑅2 = 4.8𝑅1
Adesso dobbiamo traslare il segnale di uscita di 2.5V verso l’alto. Applichiamo una tensione
continua VREF al morsetto invertente del trigger di Schmitt. Scegliamo il valore di VREF:
𝑉𝑡𝑟 = 𝑉𝑅𝐸𝐹
𝑅1 + 𝑅2
𝑅1
Sostituendo i valori numerici troviamo:
10 + 48
10
Ridisegniamo il circuito.
2.5 = 𝑉𝑅𝐸𝐹
→
2.5 = 5.8𝑉𝑅𝐸𝐹
→
𝑉𝑅𝐸𝐹 =
2.5
= 0.43𝑉
5.8
Figura 2 Schema con il trigger dimensionato.
Adesso dimensioniamo l’integratore per soddisfare le altre specifiche.
La frequenza deve essere di 2kHz calcoliamo il periodo del segnale:
𝑇=
1
1
=
= 500𝜇𝑠
𝑓 2000
Un’altra specifica ci impone che il tempo di salita sia il doppio rispetto a quello di discesa.
Indichiamo con T1 il tempo di salita e con T2 quello di discesa. Si ha:
{
500 = 𝑇1 + 𝑇2
𝑇1 = 2𝑇2
→
500 = 3𝑇2
{
𝑇1 = 2𝑇2
→
500
{𝑇2 = 3 ≈ 167
𝑇1 ≈ 333
Per avere tempi di salita e di discesa diversi dobbiamo fare in modo che il condensatore si carichi e
si scarichi attraverso due resistenze diverse. Ricorriamo ai diodi. Il circuito diventa:
Figura 3 L'integratore con il duty cycle diverso dal 50%.
2
Vediamo cosa succede. Quando l’uscita del trimmer è a livello alto il diodo D2 conduce ed il diodo
D1 è interdetto: il condensatore si carica attraverso la resistenza R4. Quando l’uscita del trimmer è a
livello basso il diodo D1 conduce ed il diodo D2 è interdetto: il condensatore si scarica attraverso la
resistenza R3. Dimensioniamo i componenti. Troviamo i due semiperiodi.
Avevamo indicato con T1 il tempo di salita. Possiamo scrivere:
𝑇1 = 2𝑅4 𝐶
𝑅1
𝑅2
Sostituendo i valori numerici:
−6
333 ∙ 10
104
= 2𝑅4 𝐶
48 ∙ 103
→
333 ∙ 10−6 = 𝑅4 𝐶
10
24
Possiamo scegliere C=10nF.
5
12
→
𝑅4 = 333 ∙ 10−6
≈ 800 ∙ 102 = 80𝑘Ω
12
5 ∙ 10−8
Procediamo nello stesso modo per dimensionare la resistenza R3.
333 ∙ 10−6 = 𝑅4 10−8
5
12
→ 𝑅4 = 167 ∙ 10−6
≈ 400 ∙ 102 = 40𝑘Ω
12
5 ∙ 10−8
Ridisegniamo il circuito con i valori trovati:
167 ∙ 10−6 = 𝑅3 10−8
Figura 4 Il circuito dimensionato.
Disegniamo, infine, gli andamenti di v0 e v+ come richiesto.
Figura 5 Le forme d'onda in ingresso ed in uscita.
3
Notiamo che l’integratore che abbiamo usato è invertente.
Questo file può essere scaricato gratuitamente. Se pubblicato citare la fonte.
Matilde Consales
4