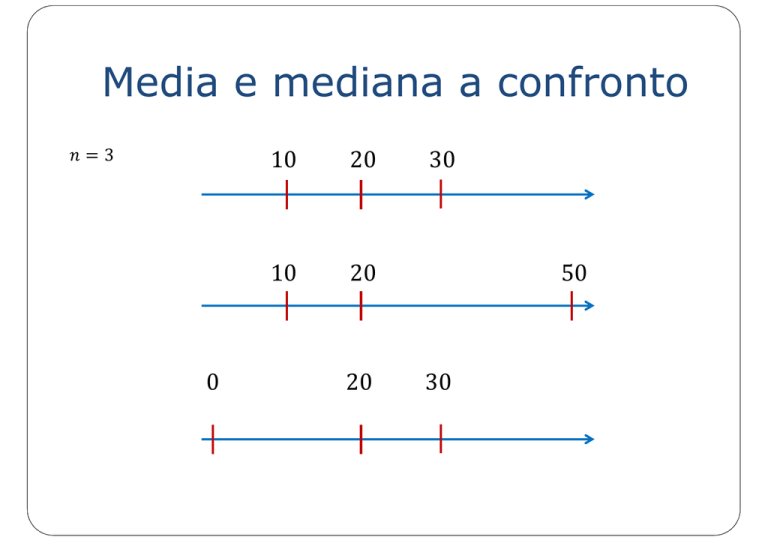
Media e mediana a confronto
=3
0
10
20
10
20
20
30
50
30
Indici di posizione
dati :
,
(
,⋯,
(
dati riordinati:
≤ ⋯≤
( ) ≤
La posizione del
)
)
= 135
= 136
( )
quartile è
Il valore della
quartile è
(IL
quartile )
+
( ⁄ )
+
(10.25)
( ⁄
)
Unità
Peso
Peso o.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
118
151
143
172
147
146
138
175
134
172
118
151
155
155
146
135
127
178
136
180
151
186
122
132
114
171
140
187
106
159
127
191
192
181
143
153
144
139
148
179
106
114
118
118
122
127
127
132
134
135
136
138
139
140
143
143
144
146
146
147
148
151
151
151
153
155
155
159
171
172
172
175
178
179
180
181
186
187
191
192
135.5
147.5
Indici di posizione
dati :
,
,⋯,
dati riordinati:
≤ ⋯≤
( ) ≤
La posizione del
( )
quartile è
Il valore della
quartile è
(IL
quartile )
!×( + )
(30.75)
(!(
)⁄ )
+
!(
)⁄
Unità
Peso
Peso o.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
118
151
143
172
147
146
138
175
134
172
118
151
155
155
146
135
127
178
136
180
151
186
122
132
114
171
140
187
106
159
127
191
192
181
143
153
144
139
148
179
106
114
118
118
122
127
127
132
134
135
136
138
139
140
143
143
144
146
146
147
148
151
151
151
153
155
155
159
171
172
172
175
178
179
180
181
186
187
191
192
135.5
147.5
172
Indici di posizione
dati :
,
Peso
Peso o.
1
2
3
4
5
6
7
8
9
10
11
118
151
143
172
147
146
138
175
134
172
118
118
118
134
138
143
146
147
151
172
172
175
= 11
,⋯,
dati riordinati:
≤ ⋯≤
( ) ≤
La posizione del
Unità
( )
quartile è
Il valore del
quartile è
(IL
quartile )
+
(3)
134
Indici di posizione
dati :
,
La posizione del
Peso
Peso o.
1
2
3
4
5
6
7
8
9
10
11
118
151
143
172
147
146
138
175
134
172
118
118
118
134
138
143
146
147
151
172
172
175
= 11
,⋯,
dati riordinati:
≤ ⋯≤
( ) ≤
Unità
( )
quartile è
Il valore del
quartile è
(IL
quartile )
!( + )
!(
)
(9)
172
Boxplot
120
140
160
180
PESO
Boxplot
Differenza (range) interquartile: Q3-Q1: IQR
180
PESO
160
Q3
media
120
140
Q2
Q1
Boxplot
Differenza (range) interquartile: Q3-Q1: IQR
PESO
180
160
media
Q2
140
è la
lunghezza massima
dei baffi
+ . # × ($! − $ )
Q3
120
. # × ($! − $ )
Q1
− . # × ($! − $ )
Boxplot
500 dati sul tempo di attesa (in minuti) presso il CUP di
un'azienda ospedaliera, dati variano da 0 a 30 minuti (range)
Quartili:
&1 = 4.5
&2 = 12.5
&3 = 21.0
0 4.5
12.5
21.0
30
Boxplot
500 dati sul tempo di attesa (in minuti) presso il CUP di
un'azienda ospedaliera, dati variano da 0 a 30 minuti (range)
'())*:
Quartili:
&1 = 4.5
1.5 × 21.0 − 4.5 = 24.75
&1 − 24.75 = −20.25 < 0
&2 = 12.5
&3 + 24.75 = 45.75 > 30
&3 = 21.0
0 4.5
12.5
21.0
30
Boxplot
500 dati sul tempo di attesa (in minuti) presso il CUP di
un'azienda ospedaliera, dati variano da 0 a 30 minuti (range)
'())*:
Quartili:
&1 = 4.5
1.5 × 21.0 − 4.5 = 24.75
&1 − 24.75 = −20.25 < 0
&2 = 12.5
&3 + 24.75 = 45.75 > 30
&3 = 21.0
0 4.5
12.5
21.0
30
5
Boxplot
estremi
3
4
outlier
Dati fuori dal baffo
(superiore): outlier
0
1
2
outlier deboli
Baffo più corto della
lunghezza massima
Boxplot
0
120
1
140
2
3
160
4
180
5
PESO
poca simmetria
simmetria
150
200
250
300
1
Boxplot …
100
2
… e istogrammi
Density
0.000
0.005
0.010
0.015
100 120 140 160 180 200
Density
0.000
0.005
0.010
0.015
0.020
100
150
200
250
300
120
140
160
180
… e istogrammi
Density
0.000
0.005
0.010
0.015
100 120 140 160 180 200
Density
0.000
0.005
0.010
0.015
0.020
100
150
200
250
100
150
200
250
300
300
250
200
0.005
100
0.010
Density
150
0.010
0.005
rappresentazione della
distribuzione delle frequenze
0.000
0.000
Density
120
140
160
0.015
180
0.015
300
0.020
… e istogrammi
100 120 140 160 180 200
100
150
200
250
300
200
0.005
100
0.010
Density
150
0.010
0.005
rappresentazione della
distribuzione delle frequenze
0.000
0.000
Density
120
140
160
300
250
rappresentazione della
dispersione dei dati
0.015
180
0.015
0.020
… e istogrammi
100 120 140 160 180 200
100
150
200
250
300
Percentili
dati :
,
dati riordinati:
≤ ⋯≤
( ) ≤
Se
Se
.</<
,⋯,
( )
+ 1 0 è intero:
+ 1 0 non è intero:
Q1: 0 = 0.25
Q2: 0 = 0.50
Q3: 0 = 0.75
1
12
+
2
13
Unità
Peso
Peso o.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
118
151
143
172
147
146
138
175
134
172
118
151
155
155
146
135
127
178
136
180
151
186
122
132
114
171
140
187
106
159
127
191
192
181
143
153
144
139
148
179
106
114
118
118
122
127
127
132
134
135
136
138
139
140
143
143
144
146
146
147
148
151
151
151
153
155
155
159
171
172
172
175
178
179
180
181
186
187
191
192
Media pesata
Media pesata
Media aritmetica:
4=
1
5
67
6
=5
67
6
×
dato
1
peso
Media pesata:
8
=5
67
6
× 96
pesi tali che:
96 > 0,
5 96 = 1
67
Media pesata
8
=5
67
6
× 96
pesi tali che:
:; <=>?. >@A;> B − ;C
96 =
,
DCD. <=>?BDB
5 96 = 1
67
30 ×
E
Stat.
+ 22 ×
E
Infor.
+ 28 ×
G
Matem.
=
E H
= 28 ( /30)
Statistica
Statistica descrittiva
INDICI
Indici di dispersione
Differenza interquartile: Q3-Q1 (IQR)
PESO
120
140
160
180
Range: Max-Min
Indici di dispersione
Prendiamo un punto di riferimento, la media,
e guardiamo a come si disperdono i dati
attorno ad esso
Indici di dispersione
Prendiamo un punto di riferimento, la media,
e guardiamo a come si disperdono i dati
attorno ad esso
−
Indici di dispersione
Prendiamo un punto di riferimento, la media,
e guardiamo a come si disperdono i dati
attorno ad esso
−
=
−
=
−
= 0 ‼‼‼!
Indici di dispersione
Prendiamo un punto di riferimento, la media,
e guardiamo a come si disperdono i dati
attorno ad esso
−
Indici di dispersione
Prendiamo un punto di riferimento, la media,
e guardiamo a come si disperdono i dati
attorno ad esso
0≤
−
MA = 0 ⟺ I DATI SONO TUTTI UGUALI!
Ex: 2, 2, 2, 2, 2 ⟹
̅=2
Indici di dispersione
Prendiamo un punto di riferimento, la media,
e guardiamo a come si disperdono i dati
attorno ad esso
=
1
−
Varianza, o scarto quadratico medio
Varianza
19 + 22 + 21 + 23 + 22 + 20
̅=
= 21.17 anni
6
Età
(y)
Peso
(kg)
Altezza
(m)
Sesso
Causa
di
morte
1
2
19
22
50.2
75.6
1.65
1.78
F
M
Nat.
Inc.
3
21
80.1
1.91
M
Inc.
4
23
56.7
1.72
M
Nat.
5
6
22
20
75.0
58.3
1.81
1.68
M
F
M.C.
Tum.
=
19 − 21.17
+ 22 − 21.17
6
Varianza
+
23 − 21.17
+ 22 − 21.17
6
+ 21 − 21.17
+ 20 − 21.17
+
= 1.81
̅ = 21.17
anni
Età
(y)
Peso
(kg)
Altezza
(m)
Sesso
Causa
di
morte
1
2
19
22
50.2
75.6
1.65
1.78
F
M
Nat.
Inc.
3
21
80.1
1.91
M
Inc.
4
23
56.7
1.72
M
Nat.
5
6
22
20
75.0
58.3
1.81
1.68
M
F
M.C.
Tum.
Varianza
* : n. figli
&
'&
0
4
1
6
2
4
3
1
' = ()
=
1
−
= 1.13
=
4 × (0 − 1.13) + 6 × (1 − 1.13) +4 × (2 − 1.13) + 1 × (3 − 1.13)
15
= 0.782
Varianza
Prendiamo un punto di riferimento, la media,
e guardiamo a come si disperdono i dati
attorno ad esso
=
1
−
=
1
−
(S.M. Iacus, Statistica)
Varianza
Tabella 2.12(b)
0
5
10
5
15
10
20
15
25
30
20
Tabella 2.12(a)
1
2
3
4
5
6
dati più frequenti vicino a 4
7
1
2
3
4
5
6
dati più frequenti lontano da 4
7
Varianza
Tabella 2.12(b)
0
5
10
5
15
10
20
15
25
30
20
Tabella 2.12(a)
1
2
3
4
5
6
dati più frequenti vicino a 4
=4
7
1
2
3
4
5
6
dati più frequenti lontano da 4
mediane pari a 4
0 =4
7
Varianza
Tabella 2.12(b)
30
20
Tabella 2.12(a)
= 4.6
0
5
10
5
15
10
20
15
25
= 2.1
1
2
3
4
5
6
dati più frequenti vicino a 4
7
1
2
3
4
5
6
dati più frequenti lontano da 4
7
Proprietà della media
0 =
+2
0 =1
0 =1
03 =
+2
03 = 1
+2
03 = 1
+2
Proprietà della varianza
0 =
+2
0 =1
0 =1
+2
4
=
5
4
=1
5
4
=1
5
Varianza campionaria
=
1
varianza della
popolazione
−
campione casuale
6̅
1
=
'−(
−
varianza
campionaria