Statistica Descrittiva
20
16
frequenza relativa
Obiettivi della lezione:
Media
Mediana, Moda
Asimmetria, kurtosi
Quantili e percentili
• devianza
• varianza
• deviazione standard
• intervallo interquartile
dispersione di una
distribuzione
12
8
dispersione
4
posizione
0
45
46.5
48
49.5
51
52.5
54
55.5
57
cm
dispersione di una distribuzione
Ore di
frequenza
sonno Maschi Femmine
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
1
3
3
7
11
8
4
2
1
-
3
6
7
8
5
3
1
1
1
1
1
1
1
1
Usando SOLO le medie possiamo
ingannarci nel confrontare i caratteri
di due gruppi di individui.
Diamo un'occhiata alla distribuzione
di frequenza della durata di sonno
indotto da un anestetico in un
campione di 40+40 pazienti.
Ad esempio , sappiamo che le donne
sono notoriamente diverse dagli uomini
sotto molti aspetti
dispersione di una distribuzione
Il periodo medio di sonno per le donne
risulta di 5 ore così come per gli uomini
Se ci soffermiamo solo sulle medie potremmo concludere che le
donne hanno una durata di sonno uguale a quello dei maschi.
Per facilitare i confronti riportiamo i dati in grafico.
15
14
13
Maschi
frequenza assoluta
12
11
Femmine
10
9
8
7
6
5
4
3
2
1
0
1
2
3
4
5
6
7
8
9
10
11
DURATA DEL SONNO INDOTTO
12
13
14
15
calcolo della media e della varianza ( dati in classi )
Nell'esempio della lunghezza dei neonati:
xi
f(xi)
45.0
46.5
48.0
49.5
51.0
52.5
54.0
55.5
57.0
2
5
7
14
16
9
5
1
1
60
xi f(xi)
( xi x ) ( xi x )2
90.0
232.5
336.0
693.0
816.0
472.5
270.0
55.5
57.0
3022.5
-5.375
-3.875
-2.375
-0.875
0.625
2.125
3.625
5.125
6.625
28.891
15.016
5.641
0.766
0.391
4.516
13.141
26.266
43.890
( xi x )2 f ( xi )
57.781
75.078
39.484
10.719
6.250
40.641
65.703
26.266
43.890
365.812
xi 2
2025.00
2162.25
2304.00
2450.25
2601.00
2756.25
2916.00
3080.25
3249.00
xi 2 f ( xi )
4050.00
10811.25
16128.00
34303.50
41616.00
24806.25
14580.00
3080.25
3249.00
152624.25
Media = 3022.5/60 = 50.375
D = (45.0-50.375)2 2 + (46.5-50.375)25+...+ (57.0-50.375)2 1 = 365.812
D = 152624.25 - (3022.5)2/60 = 152624.25 - 152258.44
Var= 365.812/59 =6.2
Deviazione standard = 2.49
= 365.813
Istogramma dei dati
20
20
frequenza relativa
ISTOGRAMMA
16
16
12
12
centro della
classe
8
8
4
4
0
0
45
•
POLIGONO DI
FREQUENZA
46.5
48
49.5
esempio della lunghezza dei neonati:
51
52.5
54
55.5
57
cm
Torniamo all’esempio del sonno
xi
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Σ
f(xi)
4
9
10
15
16
11
5
3
2
0
1
1
1
1
1
80
xi 2
1
4
9
16
25
36
49
64
81
100
121
144
169
196
225
xi f ( xi )
4
18
30
60
80
66
35
24
18
0
11
12
13
14
15
400
xi 2 f ( xi )
4
36
90
240
400
396
245
192
162
0
121
144
169
196
225
2620
( xi x ) ( xi x )2 f ( xi )
-4
64
-3
81
-2
40
-1
15
0
0
1
11
2
20
3
27
4
32
5
0
6
36
7
49
8
64
9
81
10
100
620
Media = 400/80 = 5
Devianza= 620 ; Varianza=Devianza/(N-1)= 620/79 = 7.848
Deviazione standard= 2.801
Media
5
18
Varianza
7.848101
16
dev. Stand.
2.801446
asimm.
1.456178
Kurtosi
2.897833
Mediana
5
quartile 1
3
quartile 3
6
0.25
0.2
0.1875
14
0.2
12
0.15
10
0.1375
soggetti
0.125
0.1125
8
percent
0.1
6
0.0625
4
0.05
0.05
2
0.0375
0.025
0
0
1
2
3
4
5
6
7
8
9
ore di sonno
10
0.0125
0.0125
0.0125
0.0125
0.0125
0
11
12
13
14
15
scarto semplice medio
Dato un insieme di n valori:
x1 , x2 , xn
detta
x
la loro media aritmetica e
| x1 x | | x2 x |
...
| xn x |
i valori assoluti degli scarti,
si chiama scarto semplice medio (assoluto) la media
aritmetica dei valori assoluti degli scarti semplici di ciascun
dato x dalla media aritmetica x
la varianza
Si definisce varianza di una distribuzione statistica la media
aritmetica dei quadrati degli scarti dalla media.
x1 x 2
2
2
2
... x N
N
2
Si definisce scarto quadratico medio la radice quadrata
della varianza.
2
la deviazione standard
N
Per i dati singoli =>
(xi )
2
i=1
N
Questo numero rappresenta una misura della deviazione dei valori
dalla media. Esso ci dice come i valori tendano a disperdersi intorno
alla loro media: se la deviazione standard è piccola, indica un fitto
addensamento dei valori intorno alla loro media; se è grande indica la
presenza di valori molto lontani dalla media.
m
(xi )2 f ( xi )
Per i dati raggruppati in classe =>
i=1
m
f ( xi )
i 1
Stima della Deviazione standard
N
stima in un campione =>
(xi x )
2
i=1
N-1
m
(xi x )2 f ( xi )
Per dati raggruppati in classe =>
i=1
m
f ( xi ) 1
i 1
m
dove
f ( xi ) N
i 1
Deviazione standard
ds=5.5
media
IV = 15-1 = 14
IV = 15-1 = 14
d.s = 3.6
media
IV = 15-1 = 14
d.s = 4.4
d.s = 2.7
IV = 15-1 = 14
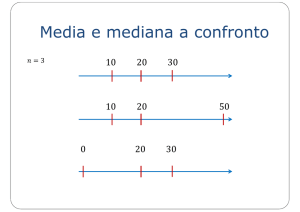
l'intervallo interquartile
Un indice di dispersione di uso comune è l'intervallo interquartile, dato
dalla differenza tra 3° e 1° quartile (cioè tra 75° e 25° centile): tale
intervallo contiene la metà dei valori inclusi nel campione,
indipendentemente dalla forma della distribuzione della variabile.
100
3° quartile
F(x)
75
mediana
50
intervallo
interquartile
1° quartile
25
0
47.25
48.75
50.25
51.75
53.25
54.75
56.25
57.75
59.25
cm
60.75
Sommario della statistica descrittiva
Obiettivi della lezione:
• media
• mediana
• moda
• percentili
• intervallo di variazione
• devianza
• varianza
• deviazione standard
• intervallo interquartile
• Indice di simmetria
• Coefficiente di variazione
La deviazione standard è una quantità utile per effettuare
confronti.
ESEMPIO: Come confrontare il vostro peso con quello di altre persone
della vostra età?
Supponiamo che uno di voi pesi 4 kg oltre la media dei soggetti della
sua età: ci sono molti altri, della stessa età, con un peso maggiore,
oppure egli è un piccolo gigante?
Bisogna conoscere la deviazione standard dei pesi dei ragazzi di quella
età, prima di fare un confronto con il peso degli altri.
Supponiamo che il peso medio dei ragazzi di quell'età sia 45 kg e che
la deviazione standard sia 2 kg:
… allora un peso di 49 kg è sopra la media di due deviazioni standard.
Approfondimento:
rivediamo alcune formule ed
introduciamo le nozioni
• di asimmetria (skewness) e
• di curtosi
Principali indici statistici
I grafici finora analizzati ci danno informazioni qualitative; possiamo
quantificarle ricorrendo ai seguenti indici.
Siano x1 , x2 ,..., xn n osservazioni numeriche
MODA
di posizione
MEDIANA
MEDIA
SCARTO QUADRATICO MEDIO
INDICI
di dispersione
VARIANZA
RANGE
di forma
ASIMMETRIA (SKEWNESS)
CURTOSI ( KURTOSIS)
Indici di posizione:
moda
media
E' definita come il valore che ha la frequenza più alta.
E' quel valore che corrisponde alla somma di tutti i
valori diviso il numero dei valori stessi.
n
X
mediana
X
i 1
n
i
dove:
Xi = esito i-ma misura
n = numero dei dati
(dimensione del campione)
E' quel valore al di sotto del quale cadono la metà dei
valori campionari.
Gli indici di posizione indicano il valore attorno al quale i dati del campione
sono posizionati
Mi interessa la dispersione dei dati intorno a tale valore
N.B. NELLA DISTRIBUZIONE NORMALE
MEDIA= MODA = MEDIANA
Indici di dispersione:
xmax -xmin
n
1
| xi - |
1
n
n
1
2
(
x
)
1 i
n
1
n
2
( xi - x )
1
n 1
1
n
2
(
x
x
)
i
n 1 1
range (intrevallo di variazione)
scarto medio assoluto
media dei quadrati degli scarti
varianza campionaria
deviazione standard campionaria
p_esimo quantile: si considera np
per [ 0 ≤ p ≤1 ]
Se np non è intero, considero k l’intero successivo e il p_esimo quantile è xk
Se np = k è intero, il p_esimo quantile è (xk+ xk+1)/2
Q1=primo quartile
Q2=secondo quartile
Q3=terzo quartile
=25° percentile
=50° percentile =mediana
=75° percentile
Media e varianza:
Media uguale
Deviazione Standard Diversa
Istogramma
80
70
60
50
40
30
20
10
0
Frequenza
Frequenza
200
150
100
Frequenza
50
9
6
3
0
8
3,
Media=2
Varianza=4
-3
2
3,
Classe
-6
6
4
1,
2,
8
0,
2
2
0
0,
Frequenza
Istogramma
Classe
Media=2
Varianza=1.33
Indici di forma
( xi )
n
3
3
INDICE DI ASIMMETRIA (Skewness)
>0 coda a destra
<0 coda a sinistra
=0 simmetrica
n
(x
i 1
i
)
n
4
4
CURTOSI
Misura il grado di ripidezza della distribuzione
>3 leptocurtica
=3 distribuzione normale (mesocurtica)
<3 platicurtica
N.B. In molti software il coefficiemte di curtosi viene confrontato con il valore 0
di di forma
di dispersione
di posizione
•media:
Indici: Schema riassuntivo
x
x
i
i
N
•moda: punto di max della distribuzione
•mediana: valore sotto al quale cadono la metà dei valori campionari. Si
dispongono i dati in ordine crescente e si prende quello che occupa la posizione
centrale (N dispari) o la media dei 2 valori in posizione centrale (N pari)
•varianza
•deviazione standard
•range
s2
i
s
xi x
2
N 1
>0 coda a ds
R xmax xmin
•skewness (coeff. di asimmetria)
xi x
i
N
<0 coda a sin
3
=0 simmetrica
x x
•curtosi: misura quanto la distribuzione è appuntita i i
<3 poco appuntita
>3 molto appuntita
N
4