sportello didattico classe terza
Classe Seconda D
Liceo ”G. Guacci” Benevento
scheda 1
22 aprile 2012
1
esercizio 1
Un’ellisse ha i fuochi nei punti F1 (4, 0) e F2 (−4, 0) e l’asse maggiore
é lungo 12.
√
Trovate le equazioni delle tangenti all’ellisse nel punto P (6, 20)
Determiniamo l’equazione canonica dell’ellisse. Siccome l’asse misura 12, allora
a = 6 e a2 = 36. Analogamente, c = 4 e c2 = 16. Dalla relazione a2 − b2 = c2
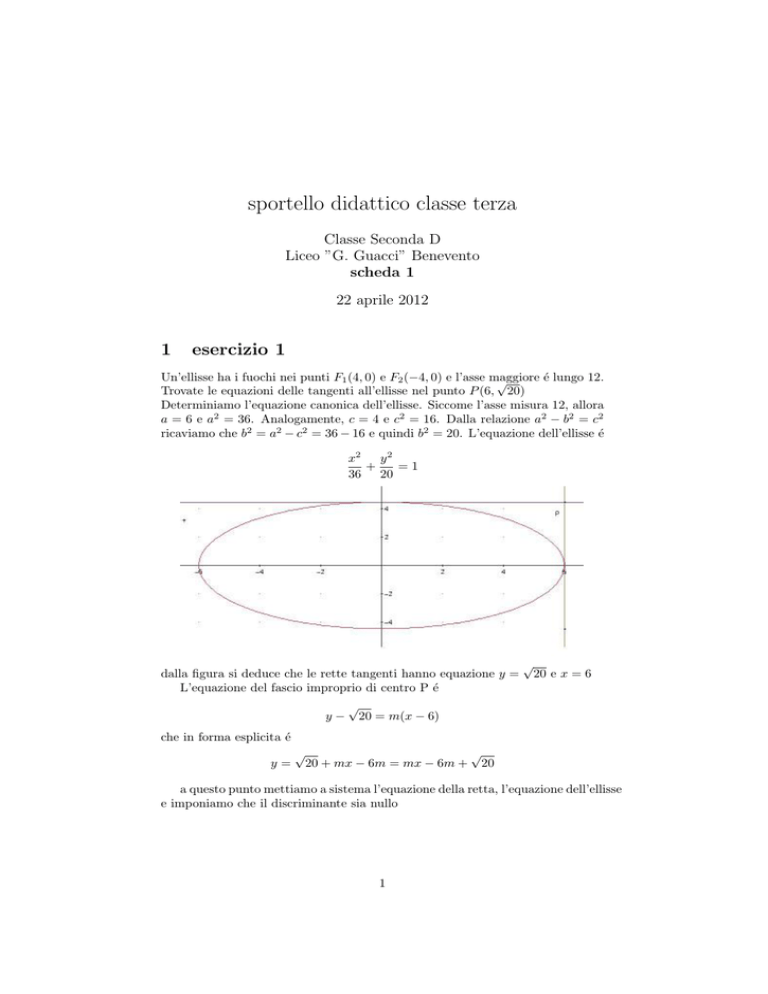
ricaviamo che b2 = a2 − c2 = 36 − 16 e quindi b2 = 20. L’equazione dell’ellisse é
x2
y2
+
=1
36 20
dalla figura si deduce che le rette tangenti hanno equazione y =
L’equazione del fascio improprio di centro P é
y−
√
√
20 e x = 6
20 = m(x − 6)
che in forma esplicita é
y=
√
20 + mx − 6m = mx − 6m +
√
20
a questo punto mettiamo a sistema l’equazione della retta, l’equazione dell’ellisse
e imponiamo che il discriminante sia nullo
1
x2
36
2
+ y20 = 1
√
y = mx − 6m + 20
∆=0
ovvero
=0
5x2 + 9y 2 − 180 √
y = mx − 6m + 20
∆=0
√ 2
5x2 + 9(mx − 6m
√+ 20) − 180 = 0
y = mx − 6m + 20
∆=0
sviluppando il quadrato
√
√
36m2 + 20 − 12m2 x + 2 20mx − 12 20m) − 180 = 0
5x2 + 9(m2 x2 + √
y = mx − 6m + 20
∆=0
moltiplichiamo per 9
√
√
2
+ 180 − 108m2 x + 18 20mx − 108 20m − 180 = 0
5x2 + 9m2 x2 + 324m
√
y = mx − 6m + 20
∆=0
raggruppiamo i termni dell’equazione
√
√
5x2 + 9m2 x2 + 324m2 + 180 − 108m2 x + 18 20mx − 108 20m − 180 = 0
√
√
(5 + 9m2 )x2 − 108m2 x + 18 20mx + 324m2 − 108 20m = 0
√
√
(5 + 9m2 )x2 + 18m( 20 − 6m)x + 108m(3m − 20) = 0
Imponiamo che il discriminante sia nullo
√
√
81m2 ( 20 − 6m)2 − 108m(3m − 20)(5 + 9m2 ) = 0
sviluppiamo le espressioni
√
√
√
81m2 (20 + 36m2 − 12 20m) − 108m(15m + 27m3 − 5 20 − 9 20m2 ) = 0
√
√
√
1620m2 +2916m4 −972 20m3 −1620m2 −2916m4 +540 20m+972 20m3 = 0
da cui
√
540 20m = 0
e quindi m = 0
da questo segue la retta tangente ha equazione y = 6 e l’altra retta tangente
ha equazione x = 6
2
2
esercizio 2
Data l’ellisse di equazione
x2
+ y2 = 1
3
conducete le tangenti
che formano un angolo di 300√con l’asse y
√
si ha che a = 3 e b = 1 quindi i vertici sono A( 3, 0) A0 (sqrt3, 0) B(0, 1) e
B 0 (0, −1).
Le tangenti appartengono a un fascio di rette improprio di equazione
y = mx + k
il nostro compito é determinare m sapendo che l’angolo che la retta forma con
la direzione -per ora positiva- dell’alsse y é di 30 gradi. In questo caso sappiamo
che m > 0.
Sia y = mx la retta del fascio improprio passante per l’origine. Il punto A(1,0)
e il puntp P(1,m). Per il teorema di Pitagora applicato al triangolo OAB é
q
2
2
2
OA + AB = OB
3
siccome OA = 1 e AB = |m − 0| = me siccome il triangolo AOB é metá di un
triangolo equilatero, é anche OB = 2OA = 2 e quindi
p
1 + m2 = 4
da cui √
m = 3 e quindi il fascio improprio di rette ha equazione
y=
√
3x + k
determiniamo le tangenti all’ellisse
2
x3 +√y 2 = 1
y = 3x + k
∆=0
da cui
2
x +√3y 2 − 3 = 0
y = 3x + k
∆=0
sostituendo
2
√
x +√3( 3x + k)2 − 3 = 0
y = 3x + k
∆=0
da cui
√
x2 + 3(3x2 + k 2 + 2k 3x) − 3 = 0
ovvero
√
x2 + 9x2 + 3k 2 + 6k 3x − 3 = 0
e quindi
√
10x2 + 6k 3x + 3(k 2 − 1) = 0
e quindi ponendo il discrimente uguale a 0
27k 2 − 30(k 2 − 1) = 0
27k 2 − 30k 2 + 30 = 0
e quindi
30 − 3k 2 = 0
e quindi
10 − k 2 = 0
da cui √
√
k1 = 10 e k2 = − 10 e quindi le rette tagenti avranno equazione
y=
√
3x +
4
√
10
y=
√
3x −
√
10
Se si considera la direzione negativa dell’asse y il problema simmetrico
rispetto all’asse x. Pertanto la soluzione sará simmetria rispetto all’asse x, e le
due rette cercate avranno equazione
√
√
y = − 3x − 10
√
√
y = − 3x + 10
5










