Esame di Campi Elettromagnetici
Prof. D’Amico – 24 settembre 2013
Traccia di soluzione
ESERCIZIO 1
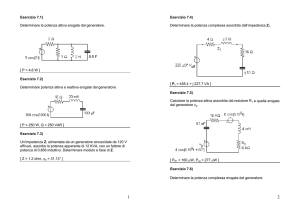
Un carico di impedenza ZL=20+j20 Ω è connesso, tramite una linea in aria di impedenza ZC=75 Ω,
attenuazione specifica α=45 dB/100m e lunghezza L=5 m, ad un generatore di impedenza interna
ZG=50 Ω e Pd=5 W. Sapendo che la frequenza di lavoro è 400 MHz, si calcoli:
a) la potenza reale fornita dal generatore;
b) la potenza reale assorbita dal carico.
B
A
ZG
ZL
ZC, α
B
L
A
Soluzione
Tenendo conto dell'attenuazione della linea, ZBB=(132+j51) Ω; di qui |Γ|=0.51 e la potenza reale
fornita dal generatore è 3.7 W.
La potenza reale che raggiunge il carico va calcolata tenendo conto che le "discontinuità" sono due
(sia nella sezione AA che BB); vanno calcolate quindi esplicitamente le onde progressiva e
regressiva che viaggiano lungo la linea di trasmissione.
ESERCIZIO 2
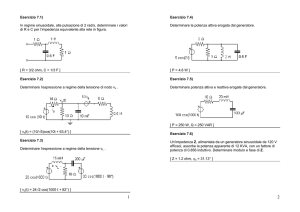
Sul multistrato dielettrico di figura incide normalmente un'onda TEM alla frequenza di 5 GHz.
Sapendo che εr1=1 ed εr3=3, calcolare:
a) il valore della costante dielettrica εr2 e lo spessore l2 affinché tutta la densità di potenza
incidente in AA venga trasmessa nel mezzo 3;
b) il modulo del campo elettrico all'interfaccia BB sapendo che SINC= 1 W/m2;
c) la densità di potenza riflessa (nel mezzo 1) se la frequenza di lavoro viene incrementata a
6 GHz (restando immutati tutti gli altri parametri).
A
εr1
B
εr2
εr3
SINC
A
l2
B
Soluzione
a) il setto adattante è un trasformatore λ/4; a conti fatti risulta εr2=1.73 e l2=11.4 mm.
b) |EBB|= 20.83 V/m.
c) Il problema si risolve notando che l2/λ=0.3 a 6 GHz e utilizzando la carta di Smith per
valutare ηAA.
ESERCIZIO 3
I due dipoli hertziani riceventi A e B di figura, lunghi 3 cm, sono connessi elettricamente in serie.
Un'onda TEM piana alla frequenza f=1 GHz incide provenendo dalla direzione θ=30o; il campo
elettrico giace sul piano del foglio ed il suo modulo vale |EINC|= 1 V/m.
Determinare:
a) la minima distanza D per la quale la potenza disponibile (ai morsetti della serie) è nulla;
b) la potenza disponibile alla frequenza f=1.3 GHz (restando immutati tutti gli altri parametri).
Einc
D
A
B
θ
x
Soluzione
a) La proiezione della distanza tra i due dipoli lungo la direzione di provenienza dell'onda deve
essere λ/2; ossia D·cos(30o)=λ/2; si trova quindi D=0.173 m.
b) Quando cambia la frequenza i due contributi di tensione non saranno più in perfetta
controfase. Tenendo conto che la connessione è in serie, la tensione sarà la somma (in
modulo e fase) delle tensioni indotte e la resistenza di radiazione la somma delle resistenze.
ESERCIZIO 4
Una spira metallica quadrata di lato a=25 cm, disposta parallelamente al piano xy, è immersa in un
campo magnetico H diretto come l'asse z (vedi figura). Il modulo del campo magnetico segue nel
tempo l'andamento indicato nel grafico. Si determini l'andamento della forza elettromotrice indotta
(FEM), in funzione del tempo (per t ≥ 0) e se ne tracci il grafico.
z
|H|
H
3 A/m
a
1 A/m
1
4
t (ns)
x
Soluzione
Essendo la FEM legata alla derivata temporale del campo magnetico H, essa risulta nulla per t ≤ 1
ns e per t ≥ 4 ns. Per 1 < t < 4 ns la derivata di H è costante e vale dH/dt=2/3 A m-1ns-1, ed è quindi
costante anche il valore della FEM (per semplicità si ignorano i punti in cui la derivata non è
continua).
Il valore del modulo si determina calcolando la circuitazione di E lungo il quadrato, ossia molto
dH
semplicemente | FEM |= µ 0 a 2
.
dt
(attenzione alle unità di misura della derivata)