EQUAZIONI
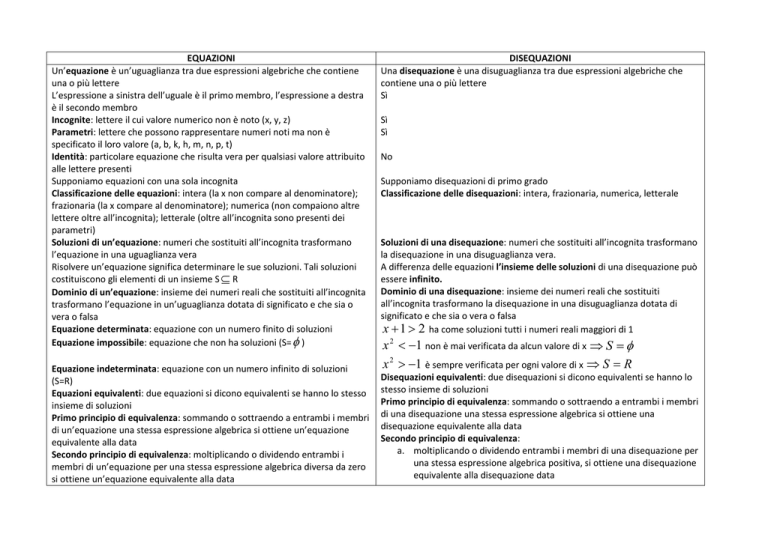
Un’equazione è un’uguaglianza tra due espressioni algebriche che contiene
una o più lettere
L’espressione a sinistra dell’uguale è il primo membro, l’espressione a destra
è il secondo membro
Incognite: lettere il cui valore numerico non è noto (x, y, z)
Parametri: lettere che possono rappresentare numeri noti ma non è
specificato il loro valore (a, b, k, h, m, n, p, t)
Identità: particolare equazione che risulta vera per qualsiasi valore attribuito
alle lettere presenti
Supponiamo equazioni con una sola incognita
Classificazione delle equazioni: intera (la x non compare al denominatore);
frazionaria (la x compare al denominatore); numerica (non compaiono altre
lettere oltre all’incognita); letterale (oltre all’incognita sono presenti dei
parametri)
Soluzioni di un’equazione: numeri che sostituiti all’incognita trasformano
l’equazione in una uguaglianza vera
Risolvere un’equazione significa determinare le sue soluzioni. Tali soluzioni
costituiscono gli elementi di un insieme S R
Dominio di un’equazione: insieme dei numeri reali che sostituiti all’incognita
trasformano l’equazione in un’uguaglianza dotata di significato e che sia o
vera o falsa
Equazione determinata: equazione con un numero finito di soluzioni
Equazione impossibile: equazione che non ha soluzioni (S= )
Equazione indeterminata: equazione con un numero infinito di soluzioni
(S=R)
Equazioni equivalenti: due equazioni si dicono equivalenti se hanno lo stesso
insieme di soluzioni
Primo principio di equivalenza: sommando o sottraendo a entrambi i membri
di un’equazione una stessa espressione algebrica si ottiene un’equazione
equivalente alla data
Secondo principio di equivalenza: moltiplicando o dividendo entrambi i
membri di un’equazione per una stessa espressione algebrica diversa da zero
si ottiene un’equazione equivalente alla data
DISEQUAZIONI
Una disequazione è una disuguaglianza tra due espressioni algebriche che
contiene una o più lettere
Sì
Sì
Sì
No
Supponiamo disequazioni di primo grado
Classificazione delle disequazioni: intera, frazionaria, numerica, letterale
Soluzioni di una disequazione: numeri che sostituiti all’incognita trasformano
la disequazione in una disuguaglianza vera.
A differenza delle equazioni l’insieme delle soluzioni di una disequazione può
essere infinito.
Dominio di una disequazione: insieme dei numeri reali che sostituiti
all’incognita trasformano la disequazione in una disuguaglianza dotata di
significato e che sia o vera o falsa
x 1 2 ha come soluzioni tutti i numeri reali maggiori di 1
x 2 1 non è mai verificata da alcun valore di x S
x 2 1 è sempre verificata per ogni valore di x S R
Disequazioni equivalenti: due disequazioni si dicono equivalenti se hanno lo
stesso insieme di soluzioni
Primo principio di equivalenza: sommando o sottraendo a entrambi i membri
di una disequazione una stessa espressione algebrica si ottiene una
disequazione equivalente alla data
Secondo principio di equivalenza:
a. moltiplicando o dividendo entrambi i membri di una disequazione per
una stessa espressione algebrica positiva, si ottiene una disequazione
equivalente alla disequazione data
Conseguenze dei principi di equivalenza
Grado di un’equazione: grado del polinomio P(x) che si ottiene dopo aver
applicato le conseguenze dei principi e scritto l’equazione nella forma
canonica P(x)=0
L’equazione di primo grado ha forma canonica:
b
b
se a 0 x
allora S
a
a
se a 0 b 0 allora S R
se a 0 b 0 allora S
ax b
b. moltiplicando o dividendo entrambi i membri di una disequazione per
una stessa espressione algebrica negativa e cambiando il verso del
simbolo di disuguaglianza, si ottiene una disequazione equivalente
alla data
Conseguenze dei principi di equivalenza
Grado di una disequazione: grado del polinomio P(x) che si ottiene dopo aver
applicato le conseguenze dei principi e scritto la disequazione in una delle
seguenti forme: P( x) 0; P( x) 0; P( x) 0; P( x) 0
La disequazione di primo grado ha una delle seguenti forme canoniche:
ax b; ax b; ax b; ax b
Per esempio se ax b
b
b
se a 0 x
allora S x R | x
a
a
b
b
se a 0 x
allora S x R | x
a
a
se a 0 b 0 0 x b sempre verificata allora S R
se a 0 b 0 0 x b mai verificata allora S