Traslazioni
y
c>0
f (x) + c
y
f (x)
f (x+k)
f (x)
f (x+k)
f (x) + c
k>0
c<0
k<0
x
O
O
x
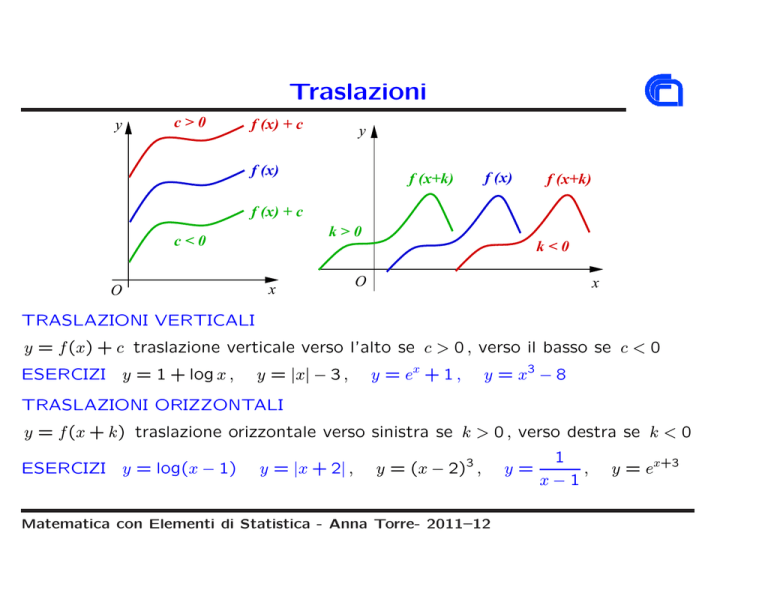
TRASLAZIONI VERTICALI
y = f (x) + c traslazione verticale verso l’alto se c > 0 , verso il basso se c < 0
ESERCIZI
y = 1 + log x ,
y = |x| − 3 ,
y = ex + 1 ,
y = x3 − 8
TRASLAZIONI ORIZZONTALI
y = f (x + k) traslazione orizzontale verso sinistra se k > 0 , verso destra se k < 0
ESERCIZI
y = log(x − 1)
y = |x + 2| ,
y = (x − 2)3 ,
Matematica con Elementi di Statistica - Anna Torre- 2011–12
y=
1
,
x−1
y = ex+3
Traslazioni
ESERCIZI Disegnare il grafico di y = 1+log x ,
ESERCIZI
y = |x|−3 ,
Disegnare il grafico di: y = log(x − 1)
y = (x − 2)3 ,
y=
1
x−1
,
y = ex + 1 ,
y = |x + 2| ,
y = ex+3
Matematica con Elementi di Statistica - Anna Torre- 2011–12
y = x3 − 8
Riflessioni
y
y
y=f(x)
O
y = f (−x )
y=f(x)
x
O
y = −f ( x )
RIFLESSIONE RISPETTO ALL’ASSE
y = −f (x)
ESERCIZI
i punti di intersezioni con l’asse x restano invariati
y = −|x| ,
1
y=− ,
x
y = log
RIFLESSIONE RISPETTO ALL’ASSE
y = f (−x)
ESERCIZI
x
1
= − log x
x
y
i punti di intersezioni con l’asse y restano invariati
√
y = e− x , y = −x , y = (−x + 1)3
Matematica con Elementi di Statistica - Anna Torre- 2011–12
x
Dilatazioni
y
y
c>1
f (k x)
c f (x)
f (x)
f (k x)
k>1
0<k<1
f (x)
0<c<1
O
c f (x)
x
CAMBIO DI SCALA SULL’ASSE
O
y
y = c · f (x)
compressione per 0 < c < 1 , dilatazione per c > 1
1
ESERCIZI y = x , y = log x3 = 3 log x , y = 5 e x
2
CAMBIO DI SCALA SULL’ASSE
x
y = f (k · x)
ESERCIZI
dilatazione per 0 < k < 1 , compressione per k > 1
√
1
y = x , y = 2 x , y = e2x
3
Matematica con Elementi di Statistica - Anna Torre- 2011–12
x
Valore Assoluto
y
y=f(x)
y
y=|f(x)|
x
O
x
O
y = |f (x)| =
f (x)
−f (x)
se f (x) ≥ 0
se f (x) < 0 ( riflessione )
NOTA gli zeri della funzione restano invariati
ESERCIZI
Disegnare il grafico di: y = |2x + 1| ,
y = |x3| ,
Matematica con Elementi di Statistica - Anna Torre- 2011–12
y = | log x|