Onde piane locali
Il campo è descrivibile in termini di onde piane TEM locali quando le sue
componenti e i parametri costitutivi del mezzo variano “abbastanza
lentamente” in funzione delle coordinate spaziali,
lentamente
spaziali nel senso che subiscono
variazioni trascurabili su lunghezze dell’ordine di λ. Si ha:
G
G
G G
G G
G G
G G
− jβ0S (r )
− jβ0S (r )
E ( r , ω ) = E0 ( r ) ⋅ e
H (r ,ω ) = H 0 (r ) ⋅ e
G
S ( r ) Funzione Iconale
((*))
Le (*) rappresentano
L
t
d
dunque
soluzioni
l i i delle
d ll equazioni
i i di Maxwell
M
ll che
h
godono (localmente) delle stesse proprietà delle onde piane TEM uniformi. Si
parla pertanto di Onde Piane TEM Locali. L’espressione del vettore di Poynting è
identica a quella valida per onde piane uniformi:
f
G 2
G G
G E × H * E0
∇S
ˆ
ˆ
=
s con s =
S=
2
2η
∇S
⇒ L’Energia si propaga lungo i raggi ottici
Come per le onde piane, anche per le onde piane locali si ha che la densità
di p
potenza ((modulo del vettore di Poynting)
y
g) vale:
1
G
G 2
I (r ) =
E0 ( r ) Intensità del raggio
2η
Ottica geometrica e disomogeneità concentrate
-Le ipotesi su cui si basa l’ottica geometrica cadono in difetto in
prossimità di superfici attraverso le quali i parametri costitutivi del
mezzo, e quindi
i di anche
h alcune
l
d ll componenti
delle
ti del
d l campo, subiscano
bi
discontinuità di prima specie (disomogeneità concentrate).
-Per aggirare il problema si ricorre ancora al concetto di onda piana locale. Si ammette
che ciascun raggio incidente sulla superficie di discontinuità abbia punto per punto un
comportamento analogo a quello di un’onda piana TEM uniforme avente in tutto lo
spazio
i le
l medesime
d i
condizioni
di i i di incidenza
i id
che
h valgono
l
l
localmente
l
t per il raggio.
i Si ha
h
quindi:
G G
G
G G
G
G G
G G
G G
1
− si ⋅ r
− si ⋅ r
= sˆi × E i ( r )
Ei ( r ) = Ei 0 ⋅ e
H i ( r ) = H i0 ⋅ e
η
G
G G
dove si = ai + jbi = (α + j β ) sˆi
sˆi direzione di incidenza
Allora ogni raggio incidente sulla superficie di discontinuità dà luogo ad un raggio
riflesso e ad un raggio trasmesso, le cui direzioni iniziali (sulla superficie di
gg di Snell della riflessione e della rifrazione.
discontinuità)) sono definite dalle leggi
Ottica geometrica e disomogeneità concentrate
Il mezzo in cui si propaga l’onda incidente è caratterizzato dai parametri
elettromagnetici μ, ε, σ. Inoltre, si possono introdurre
σ
jω
με c
L’indice di rifrazione: n =
μ 0ε 0
μ
L’impedenza
L
impedenza intrinseca del mezzo: η =
εc
Nel caso di mezzo privo di perdite e con μ = μ0, si ha:
La permittività complessa: ε c = ε +
n=
ε
= εr
ε0
questo caso,, si ha:
In q
σ =0
η=
η0
n
con η0 =
μ0
ε0
η0 impedenza di
spazio libero
G
⎧⎪α i = 0
⎧⎪ai = α i sˆi = 0
G
⇒ ⎨
⇒ ⎨ G
⎪⎩ jbi = jnβ 0 sˆi
⎪⎩ β i = bi = ω με = n β 0
il campo incidente associato all’onda TEM uniforme si può riscrivere come:
G G
G G
G
G
G
− jbi ⋅r
− jn β 0 sˆi ⋅r
⎧ Ei ( r ) = Ei 0 ⋅ e
= Ei 0 ⋅ e
⎪
G G
G
G
G
G
⎨G G
n
− jbi ⋅r
− jn β 0 sˆi ⋅r
= H i0 ⋅ e
=
sˆi × Ei
⎪ H i ( r ) = H i0 ⋅ e
η0
⎩
Esempio 1: riflessione sul terreno
¾In un radiocollegamento,
¾I
di ll
t in
i assenza di ostacoli
t li ((naturali
t li e non)) edd in
i
assenza di particolari fenomeni che si generano nell’atmosfera (effetto
condotto, inversione termica, ecc…) si hanno due contributi principali: il
raggio diretto e quello riflesso dal terreno.
terreno
1
d
2
¾Nel caso di un radiocollegamento siamo sempre in condizioni di campo
l t
lontano,
essendo
d soddisfatta
ddi f tt la
l più
iù stringente
ti
t delle:
d ll
d>>λ
d>>D
d>>2D2/ λ
p
ad un’onda ppiana e
¾In qqueste condizioni ciascun cammino corrisponde
uniforme (in realtà un’antenna emette un’onda sferica, che si può però
supporre localmente piana)
I raggi seguono delle traiettorie rettilinee.
¾Supponendo
pp
che anche la superficie
p
del suolo sia localmente ppiana,, il
raggio riflesso sul terreno soddisfa la legge della riflessione speculare.
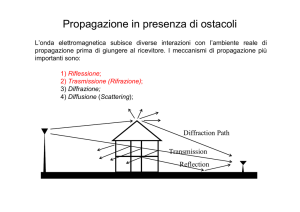
Esempio 2: propagazione in presenza di ostacoli
In ambienti complessi come quello urbano, l’onda elettromagnetica
subisce diverse interazioni con l’ambiente reale di propagazione
prima di giungere al ricevitore.
ricevitore I meccanismi di propagazione più
importanti sono:
1) Riflessione;
2) Trasmissione
T
i i
(Rif i
(Rifrazione);
)
3) Diffrazione;
4) [ Diffusione (Diffuse Scattering) ]
V
Vertex
Diff
Diffraction
i
Edge
Diffraction
Transmission
Scattering
Reflection
Riflessione e trasmissione (caso ideale)
¾ Si consideri un’onda (localmente) piana uniforme che incide sulla
superficie di separazione fra 2 mezzi omogenei. Si supponga di che tale
superficie sia approssimabile come un piano illimitato.
illimitato
¾ Nei casi pratici in cui la superficie di separazione non sia assimilabile ad un piano
si tratterà di considerare di volta in volta una porzione abbastanza piccola della
superficie da poter essere considerata piana (principio del campo locale).
locale)
¾ Si vogliono determinare i coefficienti di riflessione e trasmissione nel
caso in cui i 2 mezzi siano caratterizzati da proprietà elettromagnetiche
generiche.
Si impone la continuità delle componenti tangenti dei campi (elettrico e
magnetico)
g
) incidente,, riflesso e trasmesso sulla superficie
p
di separazione,
p
,
supponendo che su questa non vi siano correnti superficiali né impresse né
indotte (o siano talmente piccole da poter essere trascurate).
[ Si ricordi
i di che
h nell mezzo 1 vii sono il campo incidente
i id t e il campo riflesso,
ifl
mentre
t nell
mezzo 2 vi è solo campo trasmesso ]
Riflessione/Trasmissione
ŝ i
Mezzo 1
(μ0 , ε1)
X
ŝ r
θ i : angolo di incidenza
θ r : angolo
l di riflessi
ifl ione
θ t : angolo di trasmissione
θi θr
sˆi : versore onda incident
incidentee
sˆt : versore onda trasmessa
sˆr : versore onda riflessa
Mezzo 2
(μ0 , ε2)
θt
sŝ t
Ipotesi:
- Mezzi 1 e 2 omogenei [e privi di perdite]
- Interfaccia di separazione piana e infinitamente estesa
- Onda incidente piana TEM uniforme (nel mezzo 1):
G
G
G
G n1
G
G
1
− jn1 β 0 sˆi ⋅r
Ei = Ei 0 ⋅ e
; H i = sˆi × Ei = sˆi × Ei
η1
η0
Nel mezzo 2, si generano due onde piane (riflessa e rifratta)
G
G
G G
− sr ⋅r
Er = Er 0 ⋅ e
G
G
G
G
G
G G
s × Et
− st ⋅r
Et = Et 0 ⋅ e
, Ht = t
jωμ 2
G
G
G
sr × Er
, Hr =
jωμ1
Supponendo
S
d che
h anche
h lle onde
d riflessa
ifl
e rifratta
if tt siano
i
piane
i
TEM uniformi,
if
i
avremo:
G
G
G
G
G
1
− jn1 β 0 sˆr ⋅r
Er = Er 0 ⋅ e
, H r = sˆr × Er
η
G
G
G 1
G
G
− jn2 β 0 sˆt ⋅r
Et = Et 0 ⋅ e
, H t = sˆt × Et
η
Aq
questo p
punto, imponiamo
p
la continuità delle componenti
p
tangenti
g
((τ)) del
campo elettrico e magnetico totale attraverso la superficie di discontinuità.
A tal fine, è comodo adottare un sistema di riferimento ortogonale Oxyz
con ll’asse
asse x ortogonale all
all’interfaccia
interfaccia di separazione fra i 2 mezzi (figura).
Si ha:
G
G
G
Etτ
= Eiτ + Erτ
G τ − jn2 β 0 ( sty y + stz z )
G τ − jn1 β 0 ( siy y + siz z ) G τ
− jn1 β 0 ( s ry y + s rz z )
Et 0 ⋅ e
= Ei 0 ⋅ e
+ Er 0 ⋅ e
∀ y , z (1)
Una espressione analoga vale per il campo magnetico se si trascurano le
correnti superficiali:
Gτ
Gτ Gτ
Gτ Gτ Gτ
G
[ In generale, sarebbe H i + H r − H t = J S × iˆn ]
Ht ≅ Hi + H r
G τ − jnj 2 β 0 ( sty y + stz z )
G τ − jnj 1 β 0 ( siy y + siz z ) G τ − jnj 1 β 0 ( sry y + srz z )
Ht0 ⋅ e
≅ H i0 ⋅ e
+ H r0 ⋅ e
∀y , z
[ Nota: a rigore, la teoria che si svilupperà nel seguito sarebbe valida solo per
mezzi puramente dielettrici. Tuttavia, la si può estendere anche a mezzi
“debolmente conduttori” (supponendo che le correnti superficiali siano abbastanza
piccole da poter essere trascurate), e in tal caso si può tener conto delle perdite
neii mezzii attraverso
tt
l permittività
la
itti ità complessa
l
o l’indice
l’i di di rifrazione
if i
complesso.
l
]
1) Leggi della riflessione e della rifrazione
Affinché l’espressione (1) sia soddisfatta per ogni y,z deve essere:
n1siy = n1sry = n2 sty (2)
n1siz = n1srz = n2 stz (3)
Dividendo membro a membro si ottiene:
siz srz stz
=
=
= k (4) ⇒ sˆi , sˆr , sˆt
siy sry sty
complanari
l
i e appartenenti
t
ti all piano
i
di
equazione z = ky (passante per x e ⊥
alla superficie di separazione)
piano di incidenza
Aq
questo p
punto,, è conveniente adottare un riferimento cartesiano ortogonale
g
tale
che il piano di incidenza coincida con il piano xz (figura). Scomponendo i 3 versori
di propagazione delle onde incidente, riflessa e trasmessa rispetto agli assi x e z
di tale riferimento, si ottiene:
ŝ i
Allora:⎧ sˆi = − cos θ i ⋅ iˆx + sin θ i ⋅ iˆz
⎪⎪
⎨ sˆr = cos θ r ⋅ iˆx + sin θ r ⋅ iˆz
⎪
⎪⎩ sˆt = − cos θ t ⋅ iˆx + sin θ t ⋅ iˆz
Mezzo 1
(μ0 , ε1)
X
ŝ r
θi θr
Z
Mezzo 2
(μ0 , ε2)
θt
ŝ t
Sostituendo le espressioni dei versori nella (3) si ottiene:
n1 sin θi = n1 ssin
in θ r ⇒ θi = θ r LEGGE DELLA RIFLESSIONE (5)
n1 sin θi = n2 sin θt
LEGGE DI SNELL (6)
Supponiamo che n1,n2 ∈ℜ (mezzi privi di perdite) e n1>n2, dalla legge di
Snell della rifrazione si ha: θi < θt. Se si aumenta θi si arriva ad un angolo di
trasmissione θt = π/2 p
per cui si ha riflessione totale (θi = θc angolo
g
critico).
)
⎛ n2 ⎞
n1 sin θC = n2 ⇒ θC = arcsin ⎜ ⎟
⎝ n1 ⎠
Dalla (6), aumentando θi fino a superare θc, si avrebbe:
sin θ t > 1 ⇒ cos θ t = 1 − sin 2 θ t = ± j sin 2 θ t − 1
In realtà, anche se per angoli di incidenza maggiori di θc l’onda trasmessa si propaga
lungo l’asse z, nel mezzo 2 c’è comunque campo. Infatti:
G
G
G
G
− jn β − cos θ t x + sin θ t z )
− jn 2 β 0 sˆt ⋅ r
Et = Et 0 ⋅ e
=Et 0 ⋅ e 2 0 (
e infine:
G
G
−n β
Et = Et 0 ⋅ e 2 0
sin
i 2 θ t −1 x
⋅ e − jn2 β0 sinθt
z
Quindi,
Quindi: quando si verifica la riflessione totale, nel mezzo 2 si ha un’onda
trasmessa che si propaga (con andamento sinusoidale) lungo la superficie
di separazione (asse z), mentre essa si attenua in modo esponenziale nella
direzione normale alla superficie stessa (asse x).
Tale onda è detta onda evanescente.
2) Calcolo dei coefficienti di riflessione e di trasmissione
Oltre alla (2) e alla (3) bisogna imporre:
Gτ Gτ
Gτ
⎪⎧ Ei 0 + Er 0 = Et 0
Gτ
G τ (7)
⎨ Gτ
⎪⎩ H i 0 + H r 0 = H t 0
i
iˆy
(ξˆ , iˆ , sˆ ) , (ξˆ , iˆ , sˆ ) , (ξˆ , iˆ , sˆ )
y
i
r
y
r
t
y
sˆi
θΙ
ξˆr
sˆr
iˆy
θR
z
Per risolvere questo sistema scomponiamo i campi
rispetto ai riferimenti locali rappresentati in figura:
i
x
ξˆ
t
θΤ
iˆy
terne ortogonali destrorse
ξˆt
sˆt
Per un’onda piana incidente con polarizzazione generica, si avrà:
Allora:
G
⎧ Ei 0 = Ei 0ξ ξˆi + Ei 0 y iˆy
⎪⎪ G
⎨ Er 0 = Er 0ξ ξˆr + Er 0 y iˆy (8)
⎪ G
ˆ
⎪⎩ Et 0 = Et 0ξ ξt + Et 0 y iˆy
G η0
G
e ricordando H = sˆ × E :
n
n1 ⎡
⎧G
ˆy − Ei 0 yξˆi ⎤
=
H
E
i
i
i
ξ
0
0
⎪
⎦
η0 ⎣
⎪
(9)
⎨
...
⎪
⎪⎩
...
i
iˆy
sˆi
θΙ
ξˆr
sŝr
iˆy
θR
z
θΤ
iˆy
Esplicitando ξˆi , ξˆr , ξˆt in funzione di x e z si ha:
⎧ξˆi = sin θ i iˆx + cos θ i iˆz
⎪⎪
⎨ξˆr = sin θ r iˆx − cos θ r iˆz = sin θ i iˆx − cos θ i iˆz
⎪ˆ
⎪⎩ξt = sin θ t iˆx + cos θ t iˆz
x
ξˆ
(10)
ξˆt
sˆt
G G
I campi E e H si possono sempre scomporre nelle due componenti lungo ξˆ
e iˆy ,
descrivendo due soluzioni indipendenti tra loro e mutuamente esclusive,
esclusive ma
sufficienti, una volta composte, a rappresentare un campo qualsiasi!
Si tratta, in pratica, di una scomposizione del campo in 2 polarizzazioni (lineari)
ortogonali.
Per
Per
G
E // iˆy
G
E // ξˆ
G
⎡e quindi H / / −ξˆ ⎤ si parla di Polarizzazione perpendicolare (TE)
⎣
⎦
[ rispetto al piano
G
⎡e H / / iˆy ⎤ si parla di Polarizzazione parallela (TM)
di incidenza ]
⎣
⎦
( )
[ TE e TM stanno per “Trasversale Elettrica e “Trasversale Magnetica”, rispettivamente]
Nel caso TE e nel caso TM, rispettivamente, il campo incidente viene espresso dalle:
Polarizzazione TE:
Polarizzazione TM:
G TE
G
− jnβ0 sˆi ⋅r ˆ
⎧ E = Ei 0 y ⋅ e
⋅ iy
⎪
G TE
G
⎨ G TE
n1
n1
− jnβ0 sˆi ⋅r
⋅ ξˆi = H i 0ξ ξˆi
⎪ H = − η sˆi × E = − η Ei 0 y ⋅ e
0
0
⎩
G TM
G
− jnβ 0 sˆi ⋅r ˆ
⎧H = Hi0 y ⋅ e
⋅ iy
⎪
G
⎨ G TM η0 G TE
η0
− jnβ0 sˆi ⋅r
⋅ ξˆi = Ei 0ξ ξˆi
⎪ E = n H × sˆi = n H i 0 y ⋅ e
⎩
1
1
D’altra parte, le componenti dei campi tangenti alla superficie di interfaccia sono
rispettivamente,
p
nel caso di p
polarizzazione TE e TM:
G TE τ
G TE
ˆ
ˆ
E
= ix × E × iˆx = E TE
y ⋅ iy
G TE τ
G TE
H
= iˆx × H × iˆx = H zTE ⋅ iˆz
( )
( )
⎧
⎪
⎨
⎪
⎩
(
(
⎧
⎪
⎨
⎪
⎩
G TM
E
G TM
H
G TM
ˆ
= ix × E × iˆx = EzTM ⋅ iˆz
G TM
τ
ˆ
= iˆx × H ×iˆx = H TM
y ⋅ iy
)
)
τ
IImponendo
d l’uguaglianza
l’
li
d ll componenti
delle
ti tangenziali
t
i li dei
d i campii elettrici
l tt i i e
magnetici che si propagano nei 2 mezzi e sfruttando le (10), si ottiene
quindi:
1) Polarizzazione TE:
⎧ Ei 0 y + Er 0 y = Et 0 y
⎨
⎩Hi0z + H r 0z = Ht 0z
2) Polarizzazione TM:
⎧⎪ H i 0 y + H r 0 y = H t 0 y
⎨
⎪⎩ Ei 0 z + Er 0 z = Et 0 z
⎧ Ei 0 y + Er 0 y = Et 0 y
⎪
⎨ n1
n1
n2
⎪− η Ei 0 y cosθi + η Er 0 y cosθi = − η Et 0 y cosθt
0
0
⎩ 0
⎧Hi0 y + H r 0 y = Ht 0 y
⎪
⎨η0
η0
η0
H
cos
θ
−
H
cos
θ
=
H t 0 y cos θ t
i
r0 y
i
⎪ n i0 y
n1
n2
⎩ 1
1) POLARIZZAZIONE TE:
n1 ( − Ei 0 y cos θ i ) + n1 ( Er 0 y cos θ r ) = n2 ( − Et 0 y cos θ t )
Sostituendo allora la prima eq
eq. del sistema nella seconda
seconda…
−n1 Ei 0 y cosθ i + n1 Er 0 y cos θ r = −n2 ( Ei 0 y + Er 0 y ) cos θ t ⇒
Ei 0 y ( n1 cos θ i − n2 cos θ t ) = Er 0 y ( n1 cos θ i + n2 cos θ t )
Analogamente:
Ei 0 y ( n1 cos θ i − n2 cos θ t ) = ( Et 0 y − Ei 0 y ) ( n1 cos θ i + n2 cos θ t ) ⇒
2 Ei 0 y n1 cos θ i = Et 0 y ( n1 cos θ i + n2 cos θ t )
I coefficienti di riflessione e trasmissione per la polarizzazione TE valgono quindi:
ΓTE =
Er 0 y
Ei 0 y
n cosθ i − n2 cos θ t
= 1
n1 cos θ i + n2 cos θ t
Si noti che risulta:
τ TE = 1 + ΓTE
τ TE =
Et 0 y
Ei 0 y
=
2n1 cos θ i
n1 cos θ i + n2 cos θ t
Coefficienti di Fresnel
I coeff. di Fresnel si possono esprimere in funzione del solo angolo θi applicando la
legge di Snell…
2
2
⎛n
⎞
n
n ⎛n ⎞
sin θt = 1 sin θi ⇒ cos θt = 1 − ⎜ 1 sin θi ⎟ = 1 ⎜ 2 ⎟ − sin 2 θi
n2
n2 ⎝ n1 ⎠
⎝ n2
⎠
Allora…
Allora
2
ΓTE =
⎛n ⎞
n/ 1 cosθ i − n/ 1 ⎜ 2 ⎟ − sin 2 θ i
⎝ n1 ⎠
2
⎛n ⎞
n/ 1 cos θ i + n/ 1 ⎜ 2 ⎟ − sin 2 θ i
⎝ n1 ⎠
2
=
⎛n ⎞
cos θ i − ⎜ 2 ⎟ − sin 2 θ i
⎝ n1 ⎠
2
⎛n ⎞
cos θ i + ⎜ 2 ⎟ − sin 2 θ i
⎝ n1 ⎠
Utilizzando l’angolo di elevazione o di radenza θ =
π
2
τ TE = 1 + ΓTE
− θ i (usato spesso in radiotecnica)
2
ΓTE =
⎛n ⎞
sin θ − ⎜ 2 ⎟ − cos 2 θ
⎝ n1 ⎠
2
⎛n ⎞
sin θ + ⎜ 2 ⎟ − cos 2 θ
⎝ n1 ⎠
Analogamente: τ TE =
2sin θ
2
⎛ n2 ⎞
sin θ + ⎜ ⎟ − cos 2 θ
⎝ n1 ⎠
2) POLARIZZAZIONE TM:
⎧Hi0 y + H r 0 y = Ht 0 y
⎪
⎨η0
η0
η0
H
cos
θ
−
H
cos
θ
=
H t 0 y cos θ t
i
r0y
i
⎪ n i0 y
n1
n2
⎩ 1
⎧Ht 0 y = Hi0 y + H r 0 y
⎪
η0
η0
⎨η0
H
cos
H
cos
cos θ t ( H i 0 y + H r 0 y )
θ
θ
−
=
i
r0 y
i
⎪ n i0 y
n1
n2
⎩ 1
Dalla seconda, riordinando …
⎛ η0
⎞
⎛ η0
⎞
η0
η0
H i 0 y ⎜ cos θ i − cos θ t ⎟ = H r 0 y ⎜ cos θ i + cos θ t ⎟
n2
n2
⎝ n1
⎠
⎝ n1
⎠
⎛
⎞
⎛
⎞
n
n
H i 0 y ⎜ cosθ i − 1 cos θ t ⎟ = H r 0 y ⎜ cos θ i + 1 cos θ t ⎟
n2
n2
⎝
⎠
⎝
⎠
2
quindi …
ΓTM =
Hr0 y
Hi0 y
=
Er 0ξ
Ei 0ξ
2
=
2
n1 n1 ⎛ n2 ⎞
⎛ n2 ⎞
n1
2
−
⋅
−
cos
θ
sin
θ
cos θi − cos θt
⎜ ⎟
i
i ⎜
⎟
n2 n2 ⎝ n1 ⎠
n
n2
=
=
⋅ ⎝ 1 ⎠2 =
2
n1
⎛ n2 ⎞
cos θi + cos θt
n1 n1 ⎛ n2 ⎞
2
cos θi + ⋅
n2
⎜ ⎟ − sin θi ⎜ n ⎟
n2 n2 ⎝ n1 ⎠
⎝ 1⎠
2
⎛ n2 ⎞
⎛ n2 ⎞
2
cos
θ
−
−
sin
θi
⎜ ⎟
⎜ ⎟
i
⎝ n1 ⎠
⎝ n1 ⎠
2
2
⎛ n2 ⎞
⎛ n2 ⎞
2
cos
θ
+
−
sin
θi
⎜ ⎟
⎜ ⎟
i
n
n
⎝ 1⎠
⎝ 1⎠
τ TM =
Ht0 y
Hi0 y
=
Er 0ξ
Ei 0ξ
= 1 + ΓTM
Infine, considerando l’angolo di radenza:
2
Γ TM =
⎛ n2 ⎞
⎛ n2 ⎞
2
sin
θ
−
⎜ ⎟
⎜ ⎟ − cos θ
⎝ n1 ⎠
⎝ n1 ⎠
2
2
⎛n ⎞
2 ⎜ 2 ⎟ sin θ
⎝ n1 ⎠
2
2
⎛ n2 ⎞
⎛ n2 ⎞
2
sin
θ
+
−
cos
θ
⎜ ⎟
⎜ ⎟
n
n
⎝ 1⎠
⎝ 1⎠
τ TM =
2
2
⎛ n2 ⎞
⎛ n2 ⎞
2
sin
θ
+
⎜ ⎟
⎜ ⎟ − cos θ
⎝ n1 ⎠
⎝ n1 ⎠
Ponendo n = n2 n1 si possono riscrivere i coefficienti di riflessione come:
ΓTE =
cos θ i − n 2 − sin 2 θ i
ΓTM =
cos θ i + n 2 − sin 2 θ i
S il mezzo 1 è l’l’aria,
Se
i risulta
i lt n = n2 =
1
0.9
0.8
0.7
06
0.6
0.5
0.4
0.3
0.2
0.1
00
ΓTM =
cos θ i + ε r − sin θ i
2
εr=81
εr=25
εr=16
εr=9
εr=4
εr=2.56
15
30
45
60
75
Incidence angle θi (°)
TE Polarization
n 2 cos θ i + n 2 − sin 2 θ i
e quindi:
i di
Reflecttion coeffficient |Γ
ΓΤΜ |
Reflecttion coeffficient |Γ
ΓΤΕ |
ΓTE =
cos θ i − ε r − sin 2 θ i
εr
n 2 cos θ i − n 2 − sin 2 θ i
90
1
0.9
0.8
0.7
06
0.6
0.5
0.4
0.3
0.2
0.1
00
ε r cos θ i − ε r − sin 2 θ i
ε r cos θ i + ε r − sin 2 θ i
εr=81
εr=25
εr=16
εr=9
εr=4
εr=2.56
2.56
Brewster’s Angle
15
30
45
60
75
Incidence angle θi (°)
TM Polarization
90
Angolo di Brewster
•
Il coefficiente di riflessione p
per la p
polarizzazione TM si annulla q
quando è
soddisfatta la seguente condizione:
Γ TM = 0
⇒
n2 cos θ i = n1 cos θ t
•
D’altra
D’
l parte, dovendo
d
d essere verificata
ifi
anche
h la
l (6),
(6) cioè
i è la
l legge
l
di Snell
S ll
della rifrazione, si ha che:
n2 cos θ t sin θ i
=
=
(11)
n1 cos θ i sin θ t
•
L’ultima uguaglianza è verificata se e solo se risulta:
π
θi + θt =
(12)
2
Dalla (12) si ricava immediatamente:
⎛π
⎞
cos θ t = cos ⎜ − θ i ⎟ =sin θ i
⎝2
⎠
E infine, sostituendo l’ultima uguaglianza nella (11) si ottiene:
n2
tan θ i =
n1
•
Angolo di Brewster (rifrazione totale)
Per incidenza pari all’angolo di Brewster non si ha riflessione e tutta la
potenza dell
dell’onda
onda incidente passa quindi dal mezzo 1 al mezzo 2.
2 Questa
proprietà trova qualche applicazione quando si voglia limitare l’effetto delle
riflessioni.
Riepilogo
Imponendo le condizioni di continuità delle componenti tangenziali
all’interfaccia (Eiτ + Erτ = Etτ e Hiτ + Hrτ = Htτ ) si ottengono i noti risultati:
⇒ sˆi , sˆr , sˆt complanari (piano di incidenza)
⇒ Onda riflessa piana uniforme e θi = θr (legge della Riflessione)
⇒ Onda rifratta: - piana evanescente (dissociata) se n1 n2 ⋅ sin θ i ≤ 1
- piana uniforme se n1 n2 ⋅ sin θ i > 1
(n1sinθi = n2sinθt - legge di Snell della Rifrazione )
⇒ Er= Γ Ei ; Et =τ Ei
(Γ : coefficiente
ffi i t di riflessione
ifl
i
-
τ : coefficiente
ffi i t di ttrasmissione)
i i
)
Coefficienti di riflessione: riepilogo
G
E
y
G
H
G
E
θR
θΙ
G
E
z
G
H
G
H
y
θΙ
θR
z
G
E
G
H
x
x
θΤ
θΤ
¾ Polarizzazione TE = campo
elettrico polarizzato linearmente
in direzione perpendicolare al
piano di incidenza
2
ΓTE =
⎛n ⎞
cos θi − ⎜ 2 ⎟ − sin 2 θi
⎝ n1 ⎠
2
⎛n ⎞
cos θi + ⎜ 2 ⎟ − sin 2 θi
⎝ n1 ⎠
τ TE = 1 + Γ TE
¾ Polarizzazione TM = campo magnetico
polarizzato linearmente in direzione
perpendicolare al piano di incidenza ⇒
campo elettrico a polarizzazione lineare
nel piano di incidenza
ΓTM =
2
2
2
2
⎛ n2 ⎞
⎛ n2 ⎞
2
cos
θ
−
⎜ ⎟
⎜ ⎟ − sin θ i
i
⎝ n1 ⎠
⎝ n1 ⎠
⎛ n2 ⎞
⎛ n2 ⎞
2
⎜ ⎟ cos θ i + ⎜ ⎟ − sin θ i
⎝ n1 ⎠
⎝ n1 ⎠
τTM = 1 + Γ TM
Campo Elettrico Riflesso/Trasmesso
¾ Onde incidente, riflessa e rifratta piane uniformi ⇒ i raggi seguono delle traiettorie
rettilinee. Le onde riflessa e trasmessa hanno le seguenti caratteristiche:
¾ Raggio Riflesso
G
Er (s )
z
s’
⇒ Direzione di propagazione: legge della riflessione
speculare (o principio di Fermat)
θΙ θR
s
QR
QR: Punto di riflessione
x
⇒ Rappresentazione vettoriale (informazioni su intensità,
polarizzazione e fase dell’onda riflessa):
G
G TE
G TM
⎡ΓTE
E r ( s ) =E r ( s ) +E r ( s ) = ⎢
⎣ 0
G TE
0 ⎤ ⎡ Ei ( QR ) ⎤ s′ -jβs
⋅ ⎢ G TM
⋅e
⎥⋅
⎥
Γ TM ⎦ ⎢⎣ Ei ( QR ) ⎥⎦ s′+s
¾ Raggio Rifratto (Trasmesso)
z
⇒ Direzione di propagazione: legge di Snell
θΙ
s’
QR
x
θΤ s
G
Et (s )
⇒ Rappresentazione vettoriale (informazioni su intensità
intensità,
polarizzazione e fase dell’onda trasmessa):
G
G TE
G TM
⎡τ
E t ( s ) =E t ( s ) +E t ( s ) = ⎢ TE
⎣ 0
G TE
⎡
0 ⎤ E i ( QR ) ⎤ s′ -jβs
jβ
G
⋅
⋅
⋅
e
⎢
⎥
τ TM ⎥⎦ ⎢⎣ E iTM ( QR ) ⎥⎦ s′+s