Propagazione in presenza di ostacoli
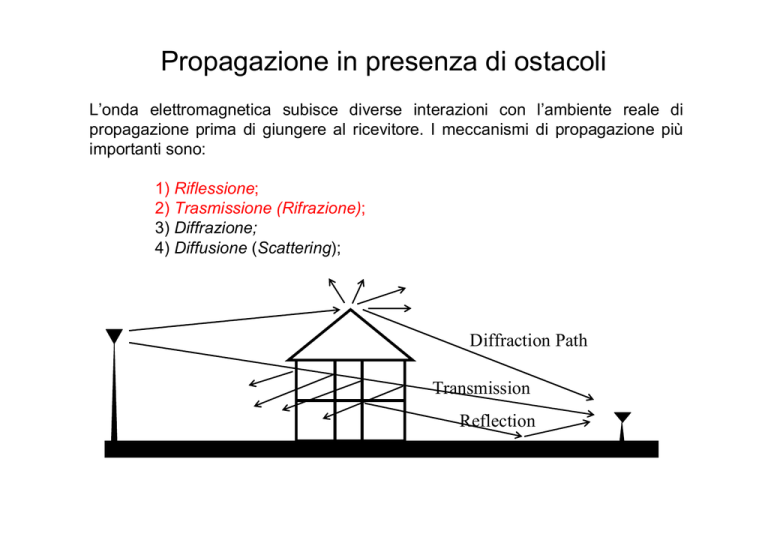
L’onda elettromagnetica subisce diverse interazioni con l’ambiente reale di
propagazione prima di giungere al ricevitore. I meccanismi di propagazione più
importanti sono:
1) Riflessione;
2) Trasmissione (Rifrazione);
3) Diffrazione;
4) Diffusione (Scattering);
Diffraction Path
Transmission
Reflection
Riflessione
¾ In un radiocollegamento, in assenza di ostacoli (naturali e non)
ed in assenza di particolari fenomeni che si generano
nell’atmosfera (effetto condotto, inversione termica, ecc…) si
hanno due contributi principali: il contributo diretto e quello
riflesso dal terreno.
1
d
2
¾ Nel caso di un radiocollegamento siamo sempre in condizioni di
campo lontano, essendo soddisfatta la più stringente delle:
¾ d>>λ
¾ d>2D2/ λ
¾ In queste condizioni ciascun cammino corrisponde ad un’onda
piana e uniforme, in realtà un’antenna emette un’onda sferica
che si può supporre localmente piana.
Riflessione e trasmissione
¾ Si consideri la superficie di separazione come un piano illimitato. Nei
casi pratici in cui la superficie di separazione non sia assimilabile ad un
piano si tratterà di considerare di volta in volta una porzione
abbastanza piccola della superficie da poter essere considerata piana.
¾ Coefficienti di riflessione e trasmissione per mezzi caratterizzati da
proprietà elettromagnetiche generiche.
¾ Si impone la continuità delle componenti tangenti dei campi (elettrico e
magnetico) incidente, riflesso e trasmesso sulla superficie di
separazione, poiché su questa non ci sono correnti superficiali né
impresse né indotte.
¾ Ricordando che nel mezzo 1 vi è il campo incidente e il campo riflesso,
mentre nel mezzo 2 vi è solo campo trasmesso
Riflessione/Rifrazione
(caso ideale)
X
(μ1 , ε1)
θI θR
θ I : angolo di incidenza
θ R : angolo di riflessione
θT : angolo di trasmissione
ŝ r
ŝ i
Sˆ I : versore onda incidente
SˆT : versore onda trasmessa
Sˆ R : versore onda riflessa
Z
(μ2 , ε2)
θT
ŝ t
n =ˆ
Hp:
-Mezzi: Aria:
εc
σ
e εc = ε +
ε0
jω
n1 ≅ 1
Terreno:
n 2 : complesso
-Interfaccia piana e infinita - mezzi omogenei
-Onda incidente piana uniforme:
r
ˆ
r
r
r
r
Si × Ei
− jn1β 0 Sˆ I ⋅r
Ei = Ei 0 ⋅ e
; Hi =
η1
Si generano 2 onde piane (riflessa e rifratta)
r
r
r r
−σ r ⋅r
Er = Er 0 ⋅ e
r
r
r r
−σ t ⋅r
Et = Et 0 ⋅ e
r
r
σ r × Er
, Hr =
jωμ1
r
r
r
σ t × Et
, Ht =
jωμ 2
r
μ
ricordando : η =
ε
Imponiamo la continuità delle componenti tangenti(τ) del campo elettrico e magnetico
totale attraverso la superficie di discontinuità:
r τ − jn2 β 0 (Sty y + Stz z ) r τ − jn1β 0 (Siy y + Siz z ) r τ − jn2 β 0 (S ry y + S rz z )
Et 0 ⋅ e
= Ei 0 ⋅ e
+ Er 0 ⋅ e
∀y, z
Espressione analoga vale per il campo Magnetico se si trascurano le componenti superficiali
Affinché l’espressione precedente sia soddisfatta per ogni y,z deve essere:
n1Siy = n1S ry = n2 Sty (2)
n1Siz = n1S rz = n2 Stz (3)
Dividendo membro a membro:
Siy
Siz
=
S ry
S rz
=
Sty
Stz
Sˆi , Sˆr , Sˆt complanari e
(4)
appartenenti al piano di incidenza
( x, y )
X
Allora:
Sˆi = − cos θ i ⋅ iˆx + sin θ i ⋅ iˆz
Sˆr = cos θ r ⋅ iˆx + sin θ r ⋅ iˆz
Sˆ = − cos θ ⋅ iˆ + sin θ ⋅ iˆ
t
t
x
t
z
(μ1 , ε1)
θI θR
ŝ r
ŝ i
Z
(μ2 , ε2)
θT
ŝ t
Sostituendo nella (3):
n1 sin θ i = n1 sin θ r ⇒ θ i = θ r (come noto)
e
n1 sin θ i = n2 sin θ t LEGGE DI SNELL (5)
Supponiamo che n1,n2 ∈ℜ e n1>n2, dalla legge di Snell si ha: θi < θt.
Se si aumenta θi si arriva ad un angolo di trasmissione θt = π/2 per cui
si ha riflessione totale (θi angolo critico).
Se si vuole propagazione lungo z, ma non attenuazione deve essere: n1,n2 ∈ℜ :
r
r
Et = Et 0 ⋅ e − jn2 β 0 (− cosθ t x +sin θt z )
Dalla (5), aumentando θi, si avrebbe:
sin θ t > 1 ⇒ cos θ t = 1 − sin 2 θ t = ± j sin 2 θ t − 1
Quindi:
r
r
− jn2 β 0
Et = Et 0 ⋅ e
sin 2 θ t −1 x
⋅e
− jn2 β 0 sin θ t z
Lungo z c’è un andamento sinusoidale, c’è propagazione, mentre lungo x c’è
Attenuazione esponenziale (onda evanescente)
Oltre alla (3) bisogna imporre:
rτ rτ
rτ
⎧ Ei 0 + Er 0 = Et 0
rτ
r τ (6)
⎨ rτ
⎩H i 0 + H r 0 = H t 0
i
iˆy
i
i
y
r
r
y
t
t
y
Ŝi
θΙ
ξˆr
θR
Ŝr
iˆy
z
Per risolvere questo sistema scomponiamo
i campi rispetto ad un riferimento locale a lato
con
(Sˆ , ξˆ , iˆ ), (Sˆ , ξˆ , iˆ ), (Sˆ , ξˆ , iˆ )
x
ξˆ
terne destrorse
θΤ
iˆy
ξˆt
Ŝt
Allora:
r
r
r
ˆ
⎧ Ei 0 = Ei 0ξ ξ i + Ei 0 y iˆy
r
r
⎪r
ˆ
⎨ Er 0 = Er 0ξ ξ r + Er 0 y iˆy
⎪ Er = Er ξˆ + Er iˆ
t 0ξ t
t0 y y
⎩ t0
(7 )
i
1
e ricordando η = η 0
n
n1 r ˆ r ˆ
⎧r
⎪⎪ H i 0 = η Ei 0ξ ξ i − Ei 0 y i y
0
(8)
⎨
...
⎪
⎪⎩
...
[
x
ξˆ
]
Esplicitando ξˆi , ξˆr , ξˆt in funzione di x e z si ha:
⎧ ξˆi = sin θ i iˆx + cos θ i iˆz
⎪ˆ
⎨ξ r = sin θ r iˆx − cos θ r iˆz = sin θ i iˆx − cos θ i iˆz
⎪ξˆ = sin θ iˆ + cos θ iˆ
t x
t z
⎩ t
iˆy
Ŝi
θΙ
ξˆr
θR
Ŝr
iˆy
z
θΤ
iˆy
ξˆt
Ŝt
r
E
Il campo
si può scomporre nelle due componenti lungo ξˆ e iˆy , descrivendo
due soluzioni indipendenti tra loro e mutuamente esclusive, ma sufficienti, una
volta composte, a rappresentare un campo qualsiasi.
Tali componenti vengono definite come: Polarizzazione del Campo.
Per
Per
r
E // iˆy
r
E // ξˆ
si parla di Polarizzazione elettrica Orizzontale (TE)
si parla di Polarizzazione elettrica Verticale (TM)
Applicando allora la continuità sulla superficie di separazione per le due
polarizzazioni rispettivamente si ha:
Polarizzazione TE:
⎧⎪ Ei 0 y + Er 0 y = Et 0 y
⎨
⎪⎩ H i 0 y + H r 0 y = H t 0 y
Polarizzazione TM:
⎧ Ei 0ξ cos θ i − Er 0ξ cos θ i = Et 0ξ cos θ t
⎪
⎨ n1 E + n1 E = n2 E
⎪ η i 0ξ η r 0ξ η t 0ξ
0
0
⎩ 0
POLARIZZAZIONE TE:
(
) (
)
(
n1 Ei 0 y cos θ i + n1 Er 0 y cos θ r = n2 − Et 0 y cos θ t
)
Sostituendo allora la prima eq. del sistema nella seconda…
(
)
n1 Ei 0 y cos θ i + n1 Er 0 y cos θ r = −n2 Ei 0 y + Er 0 y cos θ t
Ei 0 y (n1 cos θ i − n2 cos θ t ) = Er 0 y (n1 cos θ i + n2 cos θ t )
Il coefficiente di riflessione per la polarizzazione orizzontale allora vale:
n1 cos θ i − n2 cos θ t
ρO =
n1 cos θ i + n2 cos θ t
Applicando la legge di Snell…
2
⎛n
⎞
n
n
sin θ t = 1 sin θ i ⇒ cos θ t = 1 − ⎜⎜ 1 sin θ i ⎟⎟ = 1
n2
n2
⎝ n2
⎠
2
⎛ n1 ⎞
⎜⎜ ⎟⎟ − sin 2 θ i
⎝ n2 ⎠
Allora…
2
ρO =
⎛n ⎞
n/ 1 cos θ i − n/ 1 ⎜⎜ 2 ⎟⎟ − sin 2 θ i
⎝ n1 ⎠
2
⎛n ⎞
n/ 1 cos θ i + n/ 1 ⎜ 2 ⎟ − sin 2 θ i
⎝ n1 ⎠
Utilizzando l’angolo di elevazione θ =
π
2
− θ i (utilizzato spesso in radiotecnica)
2
ρO =
⎛ n2 ⎞
cos θ − ⎜⎜ ⎟⎟ − cos 2 θ
⎝ n1 ⎠
2
⎛ n2 ⎞
cos θ + ⎜⎜ ⎟⎟ − cos 2 θ
⎝ n1 ⎠
Analogamente:
τO =
2 sin θ
2
⎛n ⎞
sin θ + ⎜⎜ 2 ⎟⎟ − cos θ
⎝ n1 ⎠
POLARIZZAZIONE TM:
⎧ Ei 0ξ cos θ i − Er 0ξ cos θ i = Et 0ξ cos θ t
⎪
⎨ n1 E + n1 E = n2 E
⎪ η i 0ξ η r 0ξ η t 0ξ
0
0
⎩ 0
(
)
n1
⎧
⎪⎪ Et 0ξ = n Ei 0ξ + Er 0ξ
2
⎨
n
⎪ Ei 0ξ cos θ i − Er 0ξ cos θ i = 1 cos θ t Ei 0ξ + Er 0ξ
⎪⎩
n2
(
Dalla seconda riordinando …
⎛
⎞
⎛
⎞
n1
n1
Ei 0ξ ⎜⎜ cos θ i − cos θ t ⎟⎟ = Er 0ξ ⎜⎜ cos θ i + cos θ t ⎟⎟
n2
n2
⎝
⎠
⎝
⎠
)
quindi …
2
⎛ n2 ⎞
n1
cos θ i − cos θ t ⎜⎜ ⎟⎟ cos θ i −
n2
⎝ n1 ⎠
ρV =
=
2
n1
cos θ i + cos θ t ⎛ n2 ⎞
⎜⎜ ⎟⎟ cos θ i +
n2
⎝ n1 ⎠
Quindi considerando l’angolo di elevazione:
ρV =
τV =
2
2
⎛ n2 ⎞
⎜⎜ ⎟⎟ − cos 2 θ
⎝ n1 ⎠
2
⎛ n2 ⎞
⎜⎜ ⎟⎟ − cos 2 θ
⎝ n1 ⎠
⎛ n2 ⎞
⎜⎜ ⎟⎟ cos θ −
⎝ n1 ⎠
2
⎛ n2 ⎞
⎜⎜ ⎟⎟ cos θ +
⎝ n1 ⎠
Et 0ξ
Ei 0ξ
2
=
2
n2
sin θ
n1
⎛ n2 ⎞
⎜⎜ ⎟⎟ sin θ +
⎝ n1 ⎠
2
⎛ n2 ⎞
⎜⎜ ⎟⎟ − cos 2 θ
⎝ n1 ⎠
2
⎛ n2 ⎞
⎜⎜ ⎟⎟ − sin 2 θ i
⎝ n1 ⎠
2
⎛ n2 ⎞
⎜⎜ ⎟⎟ − sin 2 θ i
⎝ n1 ⎠
Ponendo
1
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
00
n2
n1
si possono riscrivere i coefficienti orizzontale e verticale:
cos θ i − n 2 − sin 2 θ i
cos θ i + n 2 − cos 2 θ i
ρV =
εr=81
εr=25
εr=16
εr=9
Reflection
coefficient |ρΤΜ |
Reflection coefficient |ρΤΕ |
ρO =
n=
εr=4
εr=2.56
15
30
45
θΙ
60
TE Polarization
75
90
1
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
00
n 2 cos θ i − n 2 − sin 2 θ i
n 2 cos θ i + n 2 − sin 2 θ i
εr=81
εr=25
εr=16
εr=9
εr=4
εr=2.56
15
30
45
θΙ
60
TM Polarization
75
90
Angolo di Brewster
•
Il coefficiente di riflessione per la polarizzazione elettrica verticale (TM) si
annulla per un angolo di incidenza pari a:
2
2
⎛n ⎞
⎛n ⎞
cos θ i − ⎜⎜ 1 ⎟⎟ 1 − ⎜⎜ 1 ⎟⎟ sin 2 θ i = 0
⎝ n2 ⎠
⎝ n2 ⎠
⎛n ⎞
cos 2 θ i = ⎜⎜ 1 ⎟⎟
⎝ n2 ⎠
2
⎛ ⎛ n ⎞2
⎜1 − ⎜ 1 ⎟ 1 − cos 2 θ
i
⎜ ⎜⎝ n2 ⎟⎠
⎝
(
⇒
(
)
2
⎞
⎛ ⎛ n ⎞2 ⎛ n ⎞2
⎞
⎞
⎛
n
⎟ ⇒ cos 2 θ = ⎜ 1 ⎟ ⎜1 − ⎜ 1 ⎟ + ⎜ 1 ⎟ cos 2 θ ⎟
i
i
⎜n ⎟ ⎜ ⎜n ⎟ ⎜n ⎟
⎟
⎟
2
2
2
⎠
⎝
⎠
⎝
⎠
⎝
⎠
⎝
⎠
)
⎛ ⎛ n ⎞4 ⎞ ⎛ n ⎞2 ⎛ ⎛ n ⎞2 ⎞
cos θ i ⎜ ⎜⎜ 1 ⎟⎟ − 1⎟ = ⎜⎜ 1 ⎟⎟ ⎜ ⎜⎜ 1 ⎟⎟ − 1⎟ ⇒
⎟
⎜ ⎝ n2 ⎠
⎟ ⎝ n2 ⎠ ⎜ ⎝ n2 ⎠
⎝
⎠
⎝
⎠
2
⎛n ⎞
⎛n ⎞
cos θ i = ⎜⎜ 1 ⎟⎟ 1 − ⎜⎜ 1 ⎟⎟ 1 − cos 2 θ i
⎝ n2 ⎠
⎝ n2 ⎠
⎛ ⎛ n ⎞ 2 ⎞⎛ ⎛ n ⎞ 2 ⎞ ⎛ n ⎞ 2 ⎛ ⎛ n ⎞ 2 ⎞
cos θ i ⎜ ⎜⎜ 1 ⎟⎟ − 1⎟⎜ ⎜⎜ 1 ⎟⎟ + 1⎟ = ⎜⎜ 1 ⎟⎟ ⎜ ⎜⎜ 1 ⎟⎟ − 1⎟
⎜ ⎝ n2 ⎠
⎟⎜ ⎝ n2 ⎠
⎟
⎟ ⎝ n2 ⎠ ⎜ ⎝ n2 ⎠
⎝
⎠⎝
⎝
⎠
⎠
2
2
⎛ n1 ⎞
⎜⎜ ⎟⎟
1
⎝ n2 ⎠ =
cosθ i =
2
2
⎛ n1 ⎞
⎛ n2 ⎞
⎜⎜ ⎟⎟ + 1
1 + ⎜⎜ ⎟⎟
n
⎝ 2⎠
⎝ n1 ⎠
•
Angolo di Brewster
Per incidenza pari all’angolo di Brewster non si ha riflessione e tutta la
potenza dell’onda incidente passa quindi dall’aria al terreno. Questa
proprietà trova qualche applicazione quando si voglia limitare l’effetto
delle riflessioni
Riepilogo
Imponendo la condizione di continuità all’interfaccia (Eitang + Ertang = Ettang ) si ottengono
i noti risultati:
⇒ bi , br , bt complanari (piano di incidenza)
⇒ Onda riflessa uniforme e θi = θr (legge di Snell della Riflessione);
n1 n2 ⋅ sinθ1 ≤ 1
⇒ Onda rifratta: - dissociata se
n1 n2 ⋅ sinθ1 > 1
- uniforme se
(n1sinθi=n2sin θt - legge di Snell della Rifrazione )
⇒ Er= ρ Ei ; Et =τ Ei (ρ : coefficiente di riflessione ; τ : coefficiente di trasmissione)
Onda piana locale
Il campo è descrivibile in termini di onde piane TEM locali quando le sue componenti e i
parametri costitutivi del mezzo variano “abbastanza lentamente” in funzione delle
coordinate spaziali, nel senso che subiscono variazioni trascurabili su lunghezze
dell’ordine di λ0
-Queste ipotesi su cui si basa l’ottica geometrica cadono in difetto in prossimità di
superfici attraverso le quali i parametri costitutivi del mezzo, e quindi anche alcune
delle componenti del campo, subiscano discontinuità di prima specie.
-Per aggirare il problema si ricorre ancora al concetto di onda piana locale. Si ammette
che ciascun raggio incidente sulla superficie di discontinuità abbia punto per punto un
comportamento analogo a quello di un’onda piana uniforme avente in tutto lo spazio le
medesime condizioni di incidenza che valgono localmente per il raggio:
allora ogni raggio incidente sulla superficie di discontinuità dà luogo ad un raggio
riflesso e ad uno rifratto, le cui direzioni iniziali (sulla superficie di discontinuità) sono
definite dalla legge della riflessione e dalla legge di Snell.
Onda Piana Locale
¾Analogamente l’espressione del vettore di Poynting è identica a quella valida per
onde piane uniformi.
r 2
r r
r E × H * E0
S=
=
sˆ
2
2η
¾Le
⇒
L’Energia si propaga lungo i raggi ottici
r r
r r
r
− j β 0 S (r )
E (r , ω ) = E 0 (r ) ⋅ e
r r
r r
r
− j β 0 S (r )
H (r , ω ) = H 0 (r ) ⋅ e
rappresentano dunque soluzioni delle equazioni di Maxwell che godono delle stesse
proprietà delle onde piane uniformi, dove ŝ fa le veci del versore corrispondente al
vettore d’onda.
Si parla pertanto di Onde Piani Locali.
Come per le onde piane anche per le onde piane locali vale che l’intensità
(modulo del vettore di Poynting) vale:
2
1
I=
E0
2η
Spreading Factor
¾Tubo di flusso dell’energia: superficie chiusa
costituita lateralmente da una famiglia di raggi ed
ortogonalmente da due porzioni di superficie
d’onda
Σl
dΣ2
dΣ1
¾Applicando il teorema di Poynting (conservazione
dell’energia) ad un tubo di flusso di sezioni
sufficientemente piccole da poter considerare su di esse S ≈ costante e
supponendo mezzo privo di perdite I1 ⋅ dΣ1 = I 2 ⋅ dΣ 2 Legge di intensità dell’ottica geometrica
¾L’intensità è inversamente proporzionale alle superficie di base del tubo di
flusso si definisce quindi Fattore di Divergenza:
A=
r
r
S2
E2
dΣ1
r = r = lim
E1 dΣ1 ,dΣ 2 →0 dΣ 2
S1
Tale grandezza tiene conto dell’eventuale attenuazione dovuta all’allargamento
del fronte d’onda con la propagazione. La potenza portata da ogni raggio può
diminuire con la distanza anche se il mezzo e’ privo di perdite poiché, man mano
che l’onda avanza, l’energia viene distribuita su una superficie sempre più
ampia.
Spreading Factor
¾Se mezzo omogeneo ( ⇒ propagazione per
raggi rettilinei) e onda generica (cioè sorgente
generica), si può dimostrare che :
dA
dA 0
C1
A (ρ1, ρ2 , s ) =
s
C2
ρ1
C3
C4
ρ2
ρ1 ⋅ ρ2
(ρ1 + s) ⋅ (ρ2 + s)
→ ρ1,ρ2 : raggi di curvatura principali
→ C1C2 , C3C4 : caustiche dell’onda
¾Si possono distinguere i 3 casi usuali di riferimento:
→ Onda Sferica: ρ1=ρ2 =ρ0 ⇒
A=
→ Onda Cilindrica: ρ1= ∞ , ρ2 = ρ0 ⇒
→ Onda Piana: ρ1= ρ2 = ∞ ⇒ A = 1
ρ0
ρ0 + s
A=
ρ0
ρ0 + s
Polarizzazione e fase
¾Il fattore di divergenza permette di capire come evolve l’ampiezza del campo (e
quindi la potenza) lungo il raggio ottico.
Come variano invece la fase e la polarizzazione?
¾Supponendo per semplicità mezzo omogeneo, l’equazione
del trasporto può
r
∂E0
n
essere così riscritta:
n = cos t ⇒ 0
∂s
r 2
r ⎡r 6
r 78 ⎤ 6
r 47
r 48
r
⎢
⎥
E0∇ S + 2∇S E0 ⋅ ∇ ln(n) + 2 ∇S ⋅ ∇ E0 = 0
⎢
⎥
⎣
⎦
⇓
r
∂E0 1 ⎛ ∇ 2 S ⎞ r
⎟⎟ E0 = 0
+ ⎜⎜
∂s 2 ⎝ n ⎠
(
)
¾Risolvendo tale equazione differenziale si ottiene:
r
E(s ) =
r
E
(0 )
{
Field at reference
point (s = 0)
⋅
ρ1 ⋅ ρ2
− jβ s
⋅ e
1
2
(
ρ1 + s ) ⋅ (ρ2 + s) Phase 3
factor
14442444
3
Spreading factor
Espressione vettoriale per la
propagazione del campo
lungo il raggio
Riepilogo
¾In un mezzo a indice di rifrazione lentamente variabile e privo di sorgenti nella
regione di interesse (Ji ≈ 0) , le equazioni di Maxwell ammettono soluzioni del tipo:
r r
r r − jβ S (rr )
E (r , ω ) = E0 (r ) ⋅ e 0
r r
r r − jβ S (rr )
H (r , ω ) = H 0 (r ) ⋅ e 0
¾I valori di H0 ed E0 possono essere calcolati risolvendo l’equazione del trasporto, la
funzione S(r) risolvendo invece l’equazione dell’iconale; da tale equazione e’
possibile ottenere l’equazione differenziale dei raggi, che permette di ricavare
informazioni sulle traiettorie dei raggi ottici dal solo andamento di n(r)
¾Tali soluzioni delle equazioni di Maxwell godono localmente in ogni punto delle
stesse proprietà delle onde piane uniformi ⇒ Onda Piana Locale
¾Se il mezzo e’ omogeneo, la propagazione del campo lungo un raggio e’ descritta
dalla seguente relazione
r
r
ρ1 ⋅ ρ2
− jβ s
(
)
E(s ) =
E
0
⋅
⋅
e
{
{
(ρ1 4
+ s ) ⋅ (ρ2 + s ) Phase factor
Field at reference 14
42444
3
point (s = 0)
Spreading factor
¾L’ultima espressione permette quindi di calcolare il campo in un punto Q,
partendo dal valore del campo nel punto P, da cui esce il raggio passante per
Q.
r
¾L’uso della E(s ) =
r
(0 )
E
{
Field at reference
point (s = 0)
⋅
ρ1 ⋅ ρ2
− jβ s
⋅ e
{
(ρ +4s2
)⋅ 4
(ρ24+4
s)
141 4
3 Phase factor
Spreading factor
non è ammissibile in prossimità dei punti in cui la sezione del fascio
infinitesimo preso intorno al raggio considerato si annulla; in questo caso infatti
il fattore di divergenza tende all’infinito e il campo calcolato diverge, violando le
ipotesi di lenta variabilità.
La superficie costituita dall’insieme dei punti in cui i raggi convergono si
chiama caustica e nel caso tale superficie abbia forma sferica, i raggi
convergono nel centro della sfera che viene detto fuoco.
¾I risultati dell’ottica geometrica sono quindi inaccettabili in prossimità delle
caustiche e dei fuochi.
Raggio Riflesso/Rifratto
¾ Onde diretta, riflessa e rifratta piane uniformi ⇒ immediata rappresentazione a
raggi della propagazione
¾ Raggio Riflesso
⇒ Direzione e verso : legge di Snell ( o principio di
Fermat )
θΙ θ R
x
z
⇒ Polarizzazione e fase:
r
r
r
⎡Γ
Er (s ) = ErTE (s ) + ErTM (s ) = ⎢ TE
⎣ 0
PR: punto di riflessione
r
0 ⎤ ⎡EiTE (PR )⎤ − jβs
⋅ ⎢r
⎥⋅e
ΓTM ⎥⎦ ⎣EiTM (PR )⎦
¾ Raggio Rifratto (Trasmesso)
⇒ Direzione e verso : legge di Snell
θΙ
z
θΤ
⇒ Polarizzazione e fase:
x
r
r TE
r TM
⎡τ
E t (s ) = E t (s ) + E t (s ) = ⎢ TE
⎣ 0
r
0 ⎤ ⎡EiTE (PR )⎤ − jβs
⋅ ⎢r
⎥⋅e
τTM ⎥⎦ ⎣EiTM (PR )⎦
Riflessione/Rifrazione (caso reale)
θi
θr
QR
¾ I risultati ricavati nel caso piano ideale restano validi in
situazioni realistiche più generali purché le superfici
(d’onda e di interfaccia fra i 2 mezzi) siano localmente
piane.
⇓
θt
Grandezze in gioco nel sistema (e in particolare raggi di
curvatura) >> λ
¾ L’espressione per il calcolo del campo riflesso a distanza s dal punto di riflessione
diviene pertanto (origine delle s ≡ QR):
r
r TE
r TM
⎡Γ
Er (s) = Er (s ) + Er (s ) = ⎢ TE
⎣ 0
r
0 ⎤ ⎡EiTE (PR )⎤
⋅ ⎢r
⎥⋅
ΓTM ⎥⎦ ⎣EiTM (PR )⎦
ρ1r ⋅ ρr2
⋅e − jβs
r
r
ρ1 + s ⋅ ρ2 + s
(
)(
)
ρ1r, ρ2r: raggi di curvatura principali dell’onda riflessa (dipendono dai raggi di
curvatura dell’onda incidente e della superficie di riflessione nel punto di riflessione)
¾Principio del campo locale: Il campo associato al raggio riflesso e rifratto dipende
dalle proprietà elettromagnetiche e geometriche dell’oggetto in un intorno del punto
di riflessione e dalle proprietà del campo incidente nel punto di riflessione











