TEST EQUAZIONI ESPONENZIALI E LOGARITMICHE
Le seguenti equazioni esponenziali hanno per soluzione :
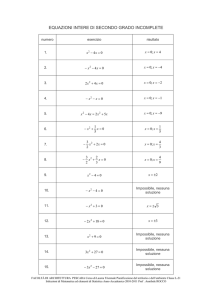
3x = 9 :
1)
x = 1;
3x =
2)
x = −2 ;
x = 2;
x = 3;
nessuna delle precedenti.
x = −2 ;
x = 2;
x = 3;
nessuna delle precedenti.
x = 2;
x = 3;
nessuna delle precedenti.
x = 0;
x = −1 ;
nessuna delle precedenti.
x = 4;
x = −4 ;
nessuna delle precedenti.
x = 1;
x = −1 ;
x = 2;
nessuna delle precedenti.
x = 1;
1
:
9
x = 1;
3 x = −9 :
3)
x = 1;
x = −2 ;
5 x +1 = 25 :
4)
x = 1;
x = 2;
25 − x = 5 − x + 4 :
5)
x = 0;
x = 2;
9 ⋅ 2x = 4 ⋅ 3x :
6)
x = 0;
4x = 8 :
7)
x = 0;
8)
2x = 5 :
x
= 0;
x
=
x=
2
;
3
2
x=− ;
3
nessuna delle precedenti.
5
log 5
log 2
; x=
; x = log ; nessuna delle precedenti.
log 2
log 5
2
Le seguenti equazioni logaritmiche hanno per soluzione :
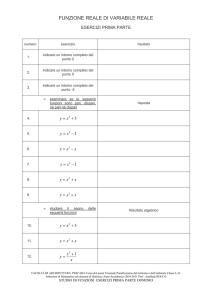
9)
log 2 x = 3 :
x
= 6;
10)
log3 x = 2 :
x
= 6;
x
x
= 9;
x = 0;
x = 8;
nessuna delle precedenti.
= 8;
x = 0;
x = 5;
nessuna delle precedenti.
FACOLTÀ DI ARCHITETTURA PESCARA Corso di Laurea Triennale Pianificazione del territorio e dell’ambiente Classe L-21
Istituzioni di Matematica ed elementi di Statistica Anno Accademico 2010-2011 Prof . Annibale ROCCO
Pagina 1 di 6
11)
log10 ( x + 2) = 1 :
x = 6;
x = 8;
x = 0;
x = 1;
nessuna delle precedenti.
x = 0;
x = 1;
nessuna delle precedenti.
12) log10 ( x + 3) = 0 :
x = −2 ;
x = −3 ;
13)
log10 ( x + 1) = log10 (−2 x + 4) :
x
= 0;
14)
log10 ( x + 2) + log10 ( x + 1) = log10 2 :
x
= 0, x = −3 ;
15)
log10 x 2 + log10 2 = log10 8 :
x
= 2;
16)
log 3 (3x − 4) = 2 :
x
= 13 ;
17)
log 6 ( 2 x − 3) = 0 :
x
= 1;
18)
log 6 ( 2 x − 4) = 0 :
x
= 1;
x
x
= 1;
x
= −2 ;
13
;
3
x = −1 ;
= −3 ;
x = 0;
x = 2, x = −2 ;
x=
3
;
13
x = 10 ;
nessuna delle precedenti.
nessuna soluzione; nessuna delle precedenti.
x
= 4, x = −4 ;
x = 3;
NP.
x = 2;
x = 3;
NP.
x = 2;
x = 3;
NP.
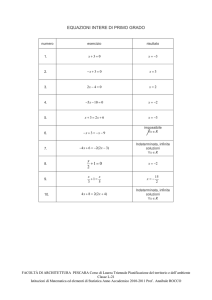
19)
log 2 ( x 2 + 3 x + 4) = 2 :
x
= 1; x = 0 ; x = 3; x = 0 ; x = −3; x = 0 ;
20)
log x ( 2 x − 1) = 2 :
x
= 1;
21)
log x + log( x − 2) = log(9 − 2 x ) :
x
= 0;
x
x
x
x
x
=
= −2 ;
= −2 ;
= 2;
= 2;
x = 0;
x = 3;
x = 0;
x = −1 ;
NP.
x = −4 ;
NP.
nessuna delle precedenti.
NP.
FACOLTÀ DI ARCHITETTURA PESCARA Corso di Laurea Triennale Pianificazione del territorio e dell’ambiente Classe L-21
Istituzioni di Matematica ed elementi di Statistica Anno Accademico 2010-2011 Prof . Annibale ROCCO
Pagina 2 di 6
FACOLTÀ DI ARCHITETTURA PESCARA Corso di Laurea Triennale Pianificazione del territorio e dell’ambiente Classe L-21
Istituzioni di Matematica ed elementi di Statistica Anno Accademico 2010-2011 Prof . Annibale ROCCO
Pagina 3 di 6
FACOLTÀ DI ARCHITETTURA PESCARA Corso di Laurea Triennale Pianificazione del territorio e dell’ambiente Classe L-21
Istituzioni di Matematica ed elementi di Statistica Anno Accademico 2010-2011 Prof . Annibale ROCCO
Pagina 4 di 6
FACOLTÀ DI ARCHITETTURA PESCARA Corso di Laurea Triennale Pianificazione del territorio e dell’ambiente Classe L-21
Istituzioni di Matematica ed elementi di Statistica Anno Accademico 2010-2011 Prof . Annibale ROCCO
Pagina 5 di 6
FACOLTÀ DI ARCHITETTURA PESCARA Corso di Laurea Triennale Pianificazione del territorio e dell’ambiente Classe L-21
Istituzioni di Matematica ed elementi di Statistica Anno Accademico 2010-2011 Prof . Annibale ROCCO
Pagina 6 di 6