Discontinuita` del campo B
In certe situazioni il campo magnetico non e`
rappresentabile da una funzione vettoriale derivabile
z
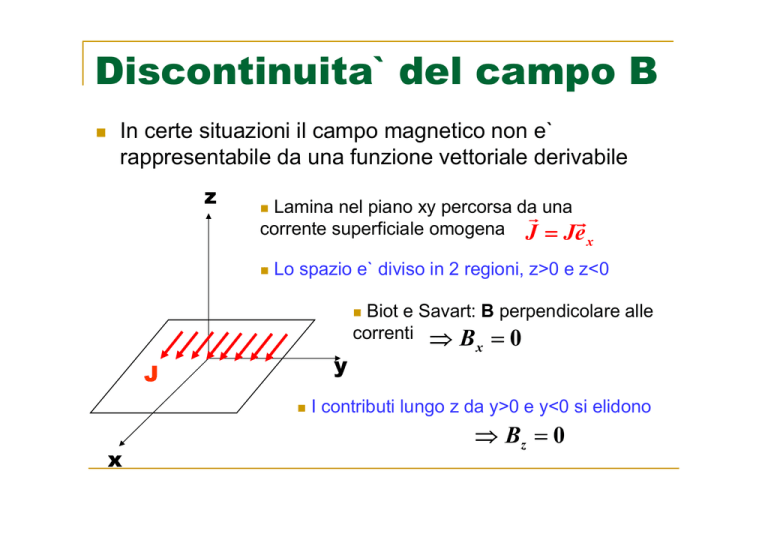
Lamina nel piano xy percorsa da una
corrente superficiale omogena J = Je
x
Lo spazio e` diviso in 2 regioni, z>0 e z<0
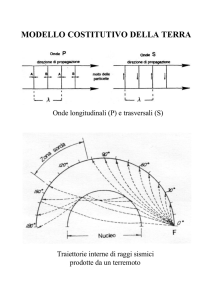
Biot e Savart: B perpendicolare alle
correnti ⇒ B = 0
x
y
J
x
I contributi lungo z da y>0 e y<0 si elidono
⇒ Bz = 0
Discontinuita` del campo B
Unica componente diversa da zero:
z
By
Circuitazione lungo un rettangolo
con lato l che taglia la corrente
Bl + ( − B )( − l ) = µ0 Jl
2Bl = µ0 Jl
y
J
l
x
B=
µ0 J
2
Discontinuita` del campo B
µ0 J B( z+ ) = −
ey
2
µ0 J B( z− ) =
ey
2
z
y
J
l
x
∆B = B( z+ ) − B( z− ) = µ0 Je y
Esempio: doppio strato
z
Le due lamine danno
contributi di segno opposto al
campo
1
B1,3 ( A) = − B1,3 ( B ) ⇒ B1,3 = 0
A
B
2
x
3
y
=0
∆B = B1 − B2 = − µ0 Je y
B2 = −∆B = µ0 Je y
Discontinuita` del campo B
Lamina nel piano xy percorsa da una
corrente superficiale omogena J = Je
z
x
Lo spazio e` diviso in 2 regioni, z>0 e z<0
∆ B = B ( z + ) − B ( z − ) = µ 0 Je y
J
x
y
Discontinuita` della componente
tangenziale del campo magnetico
Nel caso di una distribuzione
superficiale di carica elettrica la
discontinuita` e` nella componente
normale del campo magnetico
Espansione multipolare
µ0
A( r ) =
4π
∫
J ( r ')
dV '
r −r'
∫ J ( r ')dV ' → i ∫ dl '
C
Circuito chiuso
µ0 i
A( r ) =
∫C
4π dl '
r −r'
Espansione multipolare
Corrente in un circuito chiuso di dimensioni
lineari d
Potenziale vettore a grande distanza r>>d
1
1 1
= + r '⋅ ∇ ' r −r' r
r −r'
1 r '⋅ r
+⋯ = + 3 +⋯
r
r
r '= 0
µ0 i r ⋅ r ' µ0 i
A( r ) ≃
dr ' =
3
2
∫
4π C r
4π r
∫ er ⋅ r ' dr '
C
Espansione multipolare
∫
fdr = − ∫ ∇f × ndA
µ0 i Adip ( r ) =
er ⋅ r ' dr '
2 ∫
4π r C
µ0 i
=−
∇ '(er ⋅ r ') × ndA
2 ∫
4π r Σ
µ0 i µ0 e ×m
=−
e × ∫ ndA = −
2 r
2 r
4π r
4π r
Σ
µ0 µ0 m × r
Adip ( r ) =
m × er =
2
3
4π r
4π r
C
ΣC