PROBLEMA 1
ˆ si
Si considerino i triangoli la cui base è AB = 1 e il cui vertice C varia in modo che l’angolo CAB
ˆ .
mantenga doppio dell’angolo ABC
1.
Riferito il piano ad un conveniente sistema di coordinate, si determini l’equazione del luogo
geometrico γ descritto da C.
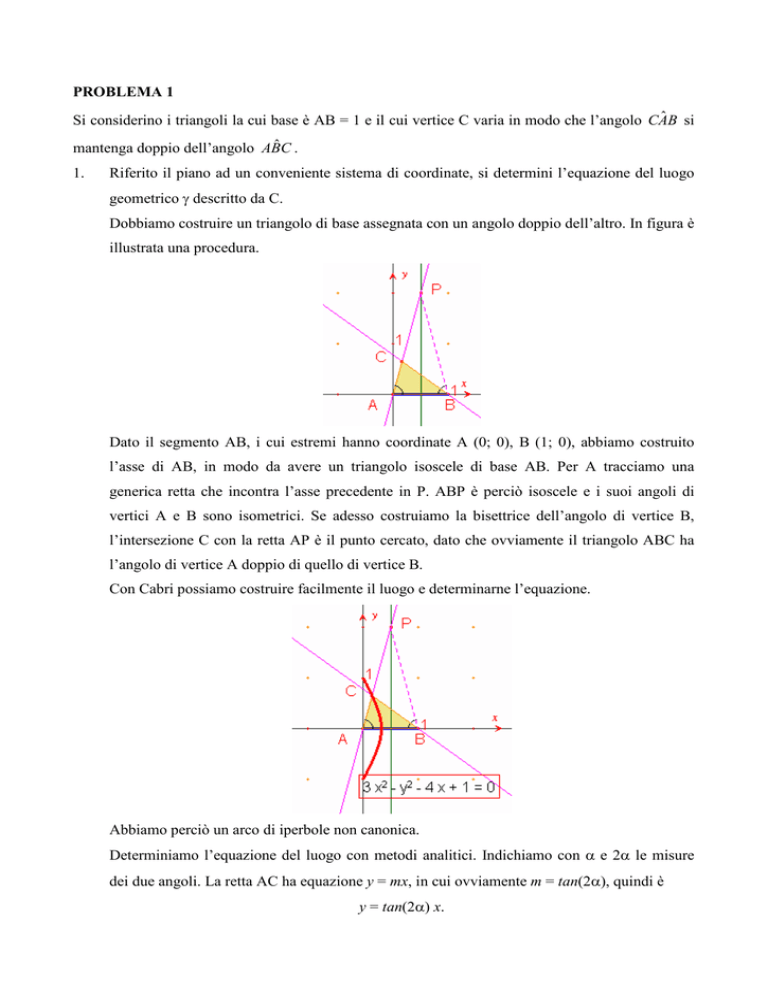
Dobbiamo costruire un triangolo di base assegnata con un angolo doppio dell’altro. In figura è
illustrata una procedura.
Dato il segmento AB, i cui estremi hanno coordinate A (0; 0), B (1; 0), abbiamo costruito
l’asse di AB, in modo da avere un triangolo isoscele di base AB. Per A tracciamo una
generica retta che incontra l’asse precedente in P. ABP è perciò isoscele e i suoi angoli di
vertici A e B sono isometrici. Se adesso costruiamo la bisettrice dell’angolo di vertice B,
l’intersezione C con la retta AP è il punto cercato, dato che ovviamente il triangolo ABC ha
l’angolo di vertice A doppio di quello di vertice B.
Con Cabri possiamo costruire facilmente il luogo e determinarne l’equazione.
Abbiamo perciò un arco di iperbole non canonica.
Determiniamo l’equazione del luogo con metodi analitici. Indichiamo con α e 2α le misure
dei due angoli. La retta AC ha equazione y = mx, in cui ovviamente m = tan(2α), quindi è
y = tan(2α) x.
La retta BC invece ha equazione
C è l’intersezione delle due rette, pertanto le sue coordinate saranno:
Che sono le equazioni parametriche del luogo. Tenendo conto della formula di duplicazione
della tangente, possiamo scrivere meglio le predette equazioni.
Ricaviamo t dalla seconda e sostituiamo nella prima.
Semplificando
Che coincide ovviamente con quella trovata da Cabri.
2.
Si rappresenti γ, tenendo conto, ovviamente, delle prescritte condizioni geometriche.
Applichiamo una traslazione di vettore (v, 0) per fare sparire il termine in x.
Con questa traslazione l’equazione diventa
Che ha la seguente rappresentazione
Se poi applichiamo la traslazione e teniamo conto dei vincoli, otteniamo l’arco di curva già
tracciato.
3.
ˆ che rende massima la somma dei quadrati delle
Si determini l’ampiezza dell’angolo ABC
altezze relative ai lati AC e BC e, con l’aiuto di una calcolatrice, se ne dia un valore
approssimato in gradi e primi (sessagesimali).
Rappresentiamo la figura.
Dobbiamo determinare tutto in funzione dell’angolo indicato, la cui misura incognita
chiamiamo x. Abbiamo AH = AB ⋅ sin ( x ) = sin ( x ) ; BK = AB ⋅ sin ( 2 x ) = sin ( 2 x ) . Quindi
dobbiamo determinare il massimo della funzione
Il vincolo è ovviamente che 0 < 3x< π, cioè 0 < x < π/3. Calcoliamo la derivata prima.
Annulliamola, nell’I.d.E.
Verifichiamo che è un punto di massimo relativo.
Il valore approssimato è
Trasformiamolo in gradi sessagesimali.
Cioè circa 52°14’.
4.
ˆ = 36° allora è AC = 5 − 1 .
Si provi che se ABC
2
ˆ = 72° , quindi anche BCA
ˆ = 72°, perciò il triangolo è
ˆ = 36°, avremo che CAB
Se ABC
isoscele e AC è la sezione aurea di AB, pertanto ha il valore indicato. Se, come è probabile, lo
studente non ricorda questo fatto, ricava AC, con il teorema dei seni.
PROBLEMA 2
Si consideri un cerchio C di raggio r.
1.
Tra i triangoli isosceli inscritti in C si trovi quello di area massima.
Il problema è noto ed è ovviamente il triangolo equilatero. Se vogliamo interpretarlo usando
l’analisi dobbiamo determinare una funzione per il calcolo dell’area di questo triangolo in
funzione di un’incognita, che sarà per noi la misura dell’angolo al vertice A, sia 2x. Pertanto
gli angoli alla base misureranno ciascuno (90° - x). Per il teorema della corda ciascuno dei lati
obliqui misurerà
2r sin(90° - x) = 2r cos(x). Infine l’area del triangolo misurerà.
Calcoliamo la derivata prima e la annulliamo.
Verifichiamo che il valore trovato fornisce un massimo relativo.
2.
Si denoti con Sn l’area del poligono regolare di n lati inscritto in C. Si dimostri che
Sn =
n 2
2π
r sen
e si trovi un’analoga espressione per l’area del poligono regolare di n lati
2
n
circoscritto a C.
Per esemplificare forniamo la figura dell’ottagono regolare inscritto.
La sua area è ovviamente data dalla somma delle aree di 8 triangoli isometrici a quello
segnato. L’angolo al centro misura, in questo caso, 2π/8 = π/4, in generale perciò sarà 2π/n.
L’area del triangolo è 1/2 r2 sin(2π/n), infine l’area del poligono regolare sarà effettivamente
Per il poligono circoscritto consideriamo come esempio sempre l’ottagono regolare.
Abbiamo ancora una volta suddiviso l’ottagono in 8 triangoli isosceli isometrici, il cui angolo
al vertice è sempre π/4, e quindi in generale 2π/n. Calcoliamo il lato obliquo in funzione del
raggio r del cerchio.
r
π
CO = AO ⋅ cos ⇒ AO =
.
π
n
cos
n
Quindi l’area del poligono circoscritto è
3.
Si calcoli il limite di Sn per n → ∞.
Ovviamente l’area del cerchio. Sarebbe interessante notare, verificando il procedimento
esaustivo, che anche la successione delle aree dei poligoni circoscritti tende allo stesso limite.
4.
Si spieghi in che cosa consista il problema della quadratura del cerchio e se, e in che senso, si
tratti di un problema risolubile o meno.
Il problema della quadratura del cerchio consiste nel costruire con riga e compasso un
quadrato che abbia area uguale a quella di un dato cerchio. Ossia, scegliendo opportunamente
l’unità di misura in modo che il raggio del cerchio sia unitario e quindi la sua area sia pari a π,
equivale a costruire un segmento di lunghezza
π . Dal punto di vista algebrico è stato
provato che con riga e compasso si possono costruire segmenti la cui misura è un numero
razionale o irrazionale quadratico, ma in generale non irrazionale cubico, per esempio non
può costruirsi
3
2 e perciò non può risolversi il problema della duplicazione del cubo. In
particolare non possono costruirsi segmenti la cui misura è rappresentata da un numero
trascendente. Nel 1882 Lindemann ha appunto provato che π è trascendente, pertanto il
problema non risolubile. Per inciso la questione appare lontana anni luce sia dai programmi
ufficiali, sia da quelli realmente svolti in qualsiasi scuola secondaria di secondo grado italiana,
anche se in questo caso, ma con diverso procedimento, i primi punti suggeriscono un’idea.
QUESTIONARIO
1.
La regione R delimitata dal grafico di y = 2 x , dall’asse x e dalla retta x = 1 (in figura) è la
base di un solido S le cui sezioni, ottenute tagliando S con piani perpendicolari all’asse x,
sono tutte triangoli equilateri. Si calcoli il volume di S.
Il volume del solido S è la somma di infiniti triangoli equilateri la cui base è lunga 2 x .
Poiché l’area di un triangolo equilatero di lato lungo t è
t2
⋅ 3 , in questo caso sarà
4
il volume è somma di queste infinite aree, cioè
2.
Le misure dei lati di un triangolo sono 40, 60 e 80 cm. Si calcolino, con l’aiuto di una
calcolatrice, le ampiezze degli angoli del triangolo, approssimandole in gradi e primi
sessagesimali.
È un semplice problema di trigonometria, una banale applicazione del teorema del coseno.
I valori sono stati trovati in radianti, abbuiamo anche verificato che la somma è un angolo
piatto.
Portiamo i valori in gradi e primi.
Quindi gli angoli misurano circa 104°29’, 46°34’, 28°57’.
3.
Si determini, al variare di k, il numero delle soluzioni reali dell’equazione:
x3 − x 2 − k + 1 = 0 .
Indipendentemente dal parametro la derivata prima si annulla sempre in due valori, uguali per
tutti.
Quindi tutte le curve hanno prima un massimo relativo e poi un minimo relativo.
Anzi il massimo è sempre maggiore del minimo, dato che 1 > 23/27. Quindi se il massimo ha
ordinata positiva e il minimo ordinata negativa, ci sono 3 soluzioni, il che accade quando
Vediamo un esempio.
Se k = 1, oppure k = 23/27, le soluzioni sono ancora tre, ma due coincidono.
In tutti gli altri casi abbiamo una soluzione, negativa per k < 23/27
E positiva per k > 1
Un altro metodo che poteva usarsi consiste nel rappresentare la cubica x3 − x 2 + 1 , quindi
rappresentare la generica retta y = k. Quindi studiare, tenendo conto dei risultati di massimo e
minimo già trovati, le intersezioni fra retta e cubica.
4.
Un serbatoio di olio ha la stessa capacità del massimo cono circolare retto di apotema 1 metro.
Si dica quanti litri di olio il serbatoio può contenere.
Dobbiamo calcolare il volume del massimo cono. Indichiamo con x la misura del raggio di
base, l’altezza è perciò
E il volume da massimizzare è
Calcoliamo la derivata prima.
Annulliamola nell’I.d.E.
Verifichiamo che è effettivamente un punto di massimo relativo.
Calcoliamo il volume.
Il valore è espresso in m3, che equivalgono a circa 403 litri.
5.
Si mostri che la funzione y = x3 + 8 soddisfa le condizioni del teorema del valor medio (o
teorema di Lagrange) sull’intervallo [-2, 2]. Si determinino i valori medi forniti dal teorema e
se ne illustri il significato geometrico.
Le condizioni sono semplicemente quelli di continuità e derivabilità, che per un polinomio
sono verificati addirittura in tutto R. Applichiamo quindi il teorema.
Abbiamo trovato due soluzioni entrambe accettabili. Calcoliamo il valore medio.
Ovviamente è lo stesso in entrambi i punti. Adesso rappresentiamo graficamente la funzione,
nel dato intervallo, le tangenti a essa nei due punti e la retta che passa per gli estremi.
6.
Si sa che il prezzo p di un abito ha subito una maggiorazione del 6% e, altresì, una
diminuzione del 6%; non si ha ricordo, però, se sia avvenuta prima l’una o l’altra delle
operazioni. Che cosa si può dire del prezzo finale dell’abito?
Ovviamente l’ordine non incide sul risultato finale, né incide il fatto che il valore dato sia 6,
ma solo che sia uguale per entrambi.
In ogni caso il prezzo è diminuito in percentuale di
.
Per una percentuale generica x avremmo avuto.
Tenuto conto che x è un valore percentuale avremmo una diminuzione di x2 per 10 000.
Anche se i valori non sono uguali l’ordine non conta. Se invece non sappiamo qual è la
percentuale di aumento e quale quella di diminuzione invece i risultati sono diversi, come si
vede per 5% e 6%.
7.
Se f(x) è una funzione reale dispari (ossia il suo grafico cartesiano è simmetrico rispetto
all’origine), definita e integrabile nell’intervallo [-2, 2], che dire del suo integrale esteso a tale
intervallo?
Ovviamente vale zero, dato che possiamo scrivere
2
∫
0
f ( x) dx =
−2
∫
−2
2
2
2
2
2
0
0
0
0
0
f ( x) dx + ∫ f ( x) dx = ∫ f (− x) dx + ∫ f ( x) dx = ∫ − f ( x) dx + ∫ f ( x) dx = 0
Del resto, per il significato geometrico dell’integrale definito, avremo due aree uguali, che
però come numeri risultano opposti, dato che una delle due è interamente nel semipiano
negativo delle y e l’altra nel semipiano positivo. Mostriamo l’esempio di x3.
8.
n
n − 2
Si risolva l’equazione 4 = 15
.
4
3
Abbiamo 4
n ⋅ ( n − 1) ⋅ ( n − 2 ) ⋅ ( n − 3)
( n − 2 ) ⋅ ( n − 3) ⋅ ( n − 4 ) , che si può scrivere
= 15
4!
3!
n ⋅ ( n − 1) ⋅ ( n − 2 ) ⋅ ( n − 3)
( n − 2 ) ⋅ ( n − 3) ⋅ ( n − 4 ) ⇒
= 15 ⋅
3!
3!
⇒ ( n − 2 ) ⋅ ( n − 3) ⋅ n ⋅ ( n − 1) − 15 ⋅ ( n − 4 ) = 0 ⇒
⇒ n = 2, n = 3, n 2 − 16n + 60 = 0 ⇒ n = 2, n = 3, n = 6, n = 10
Abbiamo inserito anche le soluzioni 2 e 3, che rappresentano coefficienti binomiali con dati
non interi positivi, che sono quelli di solito trattati nelle scuole secondarie. È vero però che
anche questi valori sono ammissibili.
Anche Derive fornisce tali valori.
9.
Si calcoli l’integrale indefinito
∫
1 − x 2 dx e, successivamente, si verifichi che il risultato di
1
∫
1 − x 2 dx è in accordo con il suo significato geometrico.
0
L’integrale è ben noto e può calcolarsi per esempio con la sostituzione x = sin(t),
Questo integrale si calcola per esempio per parti o applicando la formula di bisezione, in ogni
caso il risultato è
Che ovviamente è l’area di un quarto di cerchio di raggio 1.
10.
Per orientarsi sulla Terra si fa riferimento a meridiani e a paralleli, a latitudini e a longitudini.
Supponendo che la Terra sia una sfera S e che l’asse di rotazione terrestre sia una retta r
passante per il centro di S, come si può procedere per definire in termini geometrici meridiani
e paralleli e introdurre un sistema di coordinate geografiche terrestri?
In figura abbiamo rappresentato una sfera, il suo centro e l’asse di rotazione. Quindi abbiamo
rappresentato due cerchi massimi, l’equatore che possiamo scegliere come parallelo 0, e uno
passante per i poli, che chiamiamo meridiano 0. A questo punto ogni punto P sulla sfera è
intersezione di un meridiano e un parallelo, e può essere individuato, per esempio,
considerando gli archi PA e PB, ovviamente dopo avere stabilito un verso di lettura con
conseguente segno della misura predetta.












