1
Esercizio
(tratto dal problema 13.29 del Mazzoldi 2)
Una mole di gas ideale monoatomico compie un ciclo reversibile formato
da una trasformazione isoterma AB, una trasformazione isobara BC, e una
trasformazione adiabatica CA. Nello stato A il gas occupa un volume VA =
10−3 m3 e ha una temperatura TA = 500 K, mentre nello stato C il gas
occupa un volume VC = 2 · 10−3 m3 .
1. disegnare il ciclo nel piano p − V [2 punti];
2. determinare pressione, temperatura e volume nei tre stati A, B e C
[3 punti];
3. calcolare il lavoro svolto dal gas durante ciascuna trasformazione
[6 punti];
4. calcolare il rendimento del ciclo [4 punti];
SOLUZIONE:
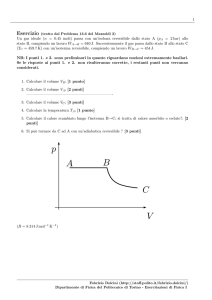
1. Notiamo che, siccome una curva adiabatica (C→A) ha pendenza maggiore di una curva isoterma (A→B), nella trasformazione isobara B→C
il volume deve necessariamente diminuire. Osservando inoltre che
VC > VA , concludiamo che il grafico del ciclo sul piano p − V è come
in figura
p
A
C
B
V
2. Per determinare le variabili termodinamiche negli stati A, B e C procediamo in questo modo:
Dr. Fabrizio Dolcini
Esercitazioni di Fisica I, Dipart. di Fisica del Politecnico di Torino
2
• Per lo stato A conosciamo TA = 500 K e VA = 10−3 m3 , e dall’equazione
di stato possiamo ricavare
pA =
nRTA
VA
(1)
Sostituendo i valori numerici
1 mol · 8.314 molJ K 500 K
=
10−3 m3
J
= 41.57 · 105 3 =
m
5 N
= 41.57 · 10 2 =
m
= 41.57 bar
pA =
(2)
• per lo stato C conosciamo il volume VC = 2 · 10−3 m3 . Dato che
la curva CA è un’adiabatica, si ha
TA VAγ−1 = TC VCγ−1
dove
γ=
cp
=
cV
5R
2
3R
2
=
5
3
(3)
(gas monoatomico)
(4)
Pertanto ricaviamo che
TC = TA
VA
VC
γ−1
= TA
VA
VC
2/3
(5)
Sostituendo i valori si ottiene
TC
2/3
1
=
= 500 K
2
= 315 K
(6)
La pressione vale
pC
=
=
=
2/3
nRTC
nR
VA
=
TA
=
VC
VC
VC
nRTA VA VA 2/3
=
VA VC VC
nRTA VA 5/3
VA
VC
(7)
Sostituendo i valori si ottiene
pC
=
1 mol · 8.314 molJ K 500 K
10−3 m3
5/3
1
=
2
= 13.09 · 105 N/m2 =
= 13.09 bar
(8)
Dr. Fabrizio Dolcini
Esercitazioni di Fisica I, Dipart. di Fisica del Politecnico di Torino
3
• Nello stato B conosciamo
TB = TA = 500 K
(9)
dato che AB è un’isoterma. Inoltre
nRTA
pB = pC =
VA
VA
VC
5/3
(10)
e dunque
pB = 13.09 bar
(11)
Dall’equazione di stato si ha
nRTB
nRTA
=
=
pB
pC
usando (7)
5/3
VC
= VA
VA
VB =
(12)
Sostituendo i valori
VB = 10−3 m3 · 25/3 =
= 3.17 · 10−3 m3
(13)
Equivalentemente VB si poteva anche determinare ricordando che,
essendo AB un’isoterma si ha
TA = TB
⇓
pA VA
nR
=
pB VB
nR
⇓
VB = VA
pA
pB
(14)
Sostituendo in (14) le eq.(1) e (10) si ottiene (12).
3. Per il calcolo del lavoro abbiamo
• trasformazione AB:
Z VB
Z
p dV =
WAB =
VA
VB
VA
nRTA
VB
dV = nRTA ln
=
V
VA
[usando (12)]
5/3
VC
= nRTA ln
=
VA
5 VC
= nRTA ln
3 VA
(15)
Dr. Fabrizio Dolcini
Esercitazioni di Fisica I, Dipart. di Fisica del Politecnico di Torino
4
Sostituendo i valori numerici
WAB = 1 mol · 8.314
= 4802 J
J
5
500 K ln 2 =
mol K
3
(lavoro eseguito dal gas)
(16)
• trasformazione BC:
WBC
= pB (VC − VB ) =
= [usando (10) e (12)]
5/3 !
VC
nRTA VA 5/3
=
VC − VA
=
VA
VC
VA
!
2/3
VA
= nRTA
−1
VC
(17)
Sostituendo i valori
WBC
J
= 1 mol · 8.314
500 K
mol K
= −1538 J
!
2/3
1
−1 =
2
(lavoro subı̀to dal gas)
(18)
• trasformazione CA:
Essendo CA una curva adiabatica (QBC = 0), dal primo principio
(∆UCA = QCA − WCA ) otteniamo che il lavoro WCA coincide con
(meno) la variazione dell’energia interna
WCA = −∆UCA = U (C) − U (A) =
[per un gas perfetto U dipende solo dalla temperatura]
= ncV (TC − TA ) =
[uso Eq.(5)]
!
2/3
VA
= ncV TA
− TA
VC
!
2/3
VA
= ncV TA
−1
VC
(19)
Sostituendo i valori numerici, e ricordando che per un gas monoatomico
cV =
3
R
2
,
(20)
si ha
WCA
3
J
= 1 mol · 8.314
500 K
2
mol K
= −2307 J
!
2/3
1
−1 =
2
(lavoro subı̀to dal gas)
(21)
Dr. Fabrizio Dolcini
Esercitazioni di Fisica I, Dipart. di Fisica del Politecnico di Torino
5
Il lavoro totale compiuto dal gas vale dunque
W = WAB + WBC + WCA
(22)
W = 4802 J − 1538 J − 2307 J = 957 J
(23)
ossia
4. Per calcolare il rendimento
η=
W
Qass
(24)
occorre valutare il calore assorbito.
• Nel tratto isotermo AB, dal primo principio abbiamo
∆UAB = 0 ⇒ QAB = WAB = 4802 J (calore assorbito) (25)
• Nel tratto isobaro BC, abbiamo
QBC
= ncp (TC − TB ) < 0 (calore ceduto)
(26)
dato che TC < TB (vedi (5) e (9))
• Nel tratto adiabatico CA, abbiamo
QCA = 0
(27)
Pertanto l’unico calore assorbito è quello nel tratto AB,ed il rendimento vale
η =
=
W
W
=
=
Qass
QAB
957 J
= 0.199
4802 J
(28)
Dr. Fabrizio Dolcini
Esercitazioni di Fisica I, Dipart. di Fisica del Politecnico di Torino