1
Esercizio
(tratto dal Problema 13.6 del Mazzoldi 2)
Un gas ideale (n = 0.45 moli) passa con un’isobara reversibile dallo stato A (pA = 2 bar) allo
stato B, compiendo un lavoro WA→B = 640 J. Successivamente il gas passa dallo stato B allo stato C
(TC = 459.7 K) con un’isoterma reversibile, compiendo un lavoro WB→C = 454 J.
NB: I punti 1. e 2. sono preliminari in quanto riguardano nozioni estremamente basilari.
Se le risposte ai punti 1. e 2. non risulteranno corrette, i restanti punti non verranno
considerati.
1. Calcolare il volume VB ; [1 punto]
2. Calcolare il volume VA ; [2 punti]
——————————————————————3. Calcolare il volume VC ; [3 punti]
4. Calcolare la temperatura TA ; [1 punto]
5. Calcolare il calore scambiato lungo l’isoterma B→C; si tratta di calore assorbito o ceduto?; [2
punti]
6. Si può tornare da C ad A con un’adiabatica reversibile ? [3 punti]
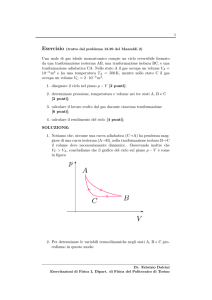
p
A
B
C
V
(R = 8.314 J mol−1 K−1 )
Fabrizio Dolcini (http://staff.polito.it/fabrizio.dolcini/)
Dipartimento di Fisica del Politecnico di Torino - Esercitazioni di Fisica I
2
SOLUZIONE
Riscriviamo i dati iniziali, in modo che tutti i dati siano espressi in unità del Sistema Internazionale.
DATI INIZIALI:
n
pA
TC
WA→B
WB→C
=
=
=
=
=
0.45 mol
2 · 105 Pa
459.7 K
640 J
454 J
1. Dall’equazione di stato dei gas perfetti, applicata allo stato B, abbiamo
pB VB = nRTB
D’altra parte sappiamo che
TB = TC
pB
VB =
⇒
nRTB
pB
(perché B→C è un’isoterma)
= pA
(perché A→B è un’isobara)
Sostituendo in (1) otteniamo:
VB =
nRTC
pA
(1)
(2)
(3)
Sostituendo i dati
VB =
J
0.45 mol
/ · 8.314 mol
/
/ K
/ 459.7 K
2 · 105 Pa
J
= 8.60 · 10−3
=
Pa
[uso J= Nm e Pa=N/m2 ]
=
= 8.60 · 10−3 m3
(4)
2. Dall’espressione del lavoro, applicata alla trasformazione A→B, abbiamo
WA→B =
Z
VB
p dV =
VA
= [A→B è un’isobara ⇒ p non dipende dal volume, è costante]
Z VB
=
p
dV =
|{z} VA
=pA =pB
= pA (VB − VA )
(5)
da cui
VA = VB −
WA→B
pA
(6)
Fabrizio Dolcini (http://staff.polito.it/fabrizio.dolcini/)
Dipartimento di Fisica del Politecnico di Torino - Esercitazioni di Fisica I
3
Sostituendo i dati
VA = VB −
WA→B
=
pA
640 J
2 · 105 Pa
[uso J= Nm e Pa=N/m2 ]
= 8.60 · 10−3 m3 −
= 5.40 · 10−3 m3
(7)
3. Dall’espressione del lavoro per l’isoterma da B a C, otteniamo:
Z VC
WB→C =
p dV =
VB
[lungo un’isoterma p non è costante, ma dipende da V ,
quindi non possiamo portarla fuori dall’integrale. Uso
allora l’equazione di stato.]
Z VC
nRT
=
dV =
V
VB
[lungo un’isoterma T è costante]
Z VC
dV
=
= nR |{z}
T
V
VB
=TB =TC
= nRTC ln
VC
VB
(8)
Quindi abbiamo
WB→C
= nRTC ln
VC
VB
⇓
WB→C
nRTC
= ln
VC
VB
⇓
e
WB→C
nRTC
(prendo l’esponenziale di ambo i membri)
VC
=
VB
(9)
Pertanto
VC = VB e
WB→C
nRTC
(10)
Sostituendo i dati
VC
= 8.60 · 10−3 m3 exp
454 J/
J
/
0.45mol
/ · 8.314 mol
/
K
/
459.7 K
/
=
[Controllo dimensionale: l’argomento di un exp deve essere adimensionale,
semplifico le unità di misura]
454
−3 3
= 8.60 · 10 m exp
=
0.45 · 8.314 · 459.7
|
{z
}
adimensionale: OK
= 8.60 · 10−3 m3 · 1.302
= 11.20 · 10−3 m3
(11)
Fabrizio Dolcini (http://staff.polito.it/fabrizio.dolcini/)
Dipartimento di Fisica del Politecnico di Torino - Esercitazioni di Fisica I
4
4. Per calcolare la temperatura TA utilizziamo nuovamente l’equazione di stato
pA VA = nRTA
da cui
TA =
pA VA
nR
(12)
(13)
Sostituendo i dati, e utilizzando (7)
TA =
2.0 · 105 Pa · 5.40 · 10−3 m3
=
J
0.45 mol
/ · 8.314 mol
/ K
[uso J=Pa m3 ]
= 288.67 K
(14)
5. Per calcolare il calore scambiato lungo l’isoterma B→C utilizziamo il primo principio
∆UB→C = QB→C − WB→C
(15)
Ricordando che per un gas perfetto l’energia interna U dipende solo dalla temperatura
U = n cV T
notiamo che
∆UB→C = n cV (TC − TB ) = 0 ,
(16)
in quanto B→C è un’isoterma. Pertanto da (15) abbiamo che
QB→C = WB→C = 454 J
(17)
Essendo Q > 0 si tratta di calore assorbito. Infatti durante B→C il gas si espande e compie
lavoro: dato che l’energia interna rimane costante il lavoro viene compiuto assorbendo calore.
6. Le trasformazioni adiabatiche (reversibili) sono caratterizzate da equazioni
pV γ = cost
(adiabatiche rev.)
Siccome γ = cp /cV > 1, nel piano p-V le curve delle trasformazioni adiabatiche hanno una
pendenza maggiore rispetto alle curve isoterme, che sono invece caratterizzate da equazioni
pV = cost
(isoterme)
Osservo che lo stato A, rispetto allo stato C, è caratterizzato da:
VA < VC
TA < TC
(18)
Partendo dal punto che identifica lo stato C nel piano p-V (vedi Fig.1), l’adiabatica che passa
per C ha pendenza maggiore dell’isoterma BC. Di conseguenza, se ci si muove da C lungo tale
adiabatica diminuendo il volume, la temperatura del gas aumenta; e se ci si muove lungo tale
adiabatica verso temperature piú basse (zona azzurra) il volume aumenta.
In nessun caso si può dunque tornare allo stato A muovendosi lungo un’adiabatica reversibile
che parte da C.
Fabrizio Dolcini (http://staff.polito.it/fabrizio.dolcini/)
Dipartimento di Fisica del Politecnico di Torino - Esercitazioni di Fisica I
5
V
B
A
T
T
T
<
TC
=
>
TC
TC
C
p
Figure 1: Nel piano p-V le adiabatiche reversibili (pV γ = const, curve blu tratteggiate) hanno
pendenza maggiore rispetto alle isoterme (pV = const, curve rosse continue). L’isoterma BC divide il
piano p-V in due regioni: quella delle basse temperature T < TC (regione azzurra in basso a sinistra)
e quella delle alte temperature T > TC (regione arancio in alto a destra).
Fabrizio Dolcini (http://staff.polito.it/fabrizio.dolcini/)
Dipartimento di Fisica del Politecnico di Torino - Esercitazioni di Fisica I