Nome file k:\scuola\corsi\corso fisica\elettromagnetismo\forza di lorentz\forza di lorentz su cariche in moto.doc
Elaborato il 04/03/2004 alle ore 17.39.26, salvato il 04/03/04 17.27
Creato il 04/03/2004 17.24.00
stampato il 04/03/2004 17.39.00
Dimensione file: 48640 byte
Web: http://digilander.iol.it/profzucchini
Interazioni cariche-campi magnetici statici
Le prime indicazione dell’interazione delle cariche elettriche in movimento con i campi magnetici statici
riguardano sia cariche singole (forza di Lorentz) che fili percorsi da correnti.
Forza di Lorentz
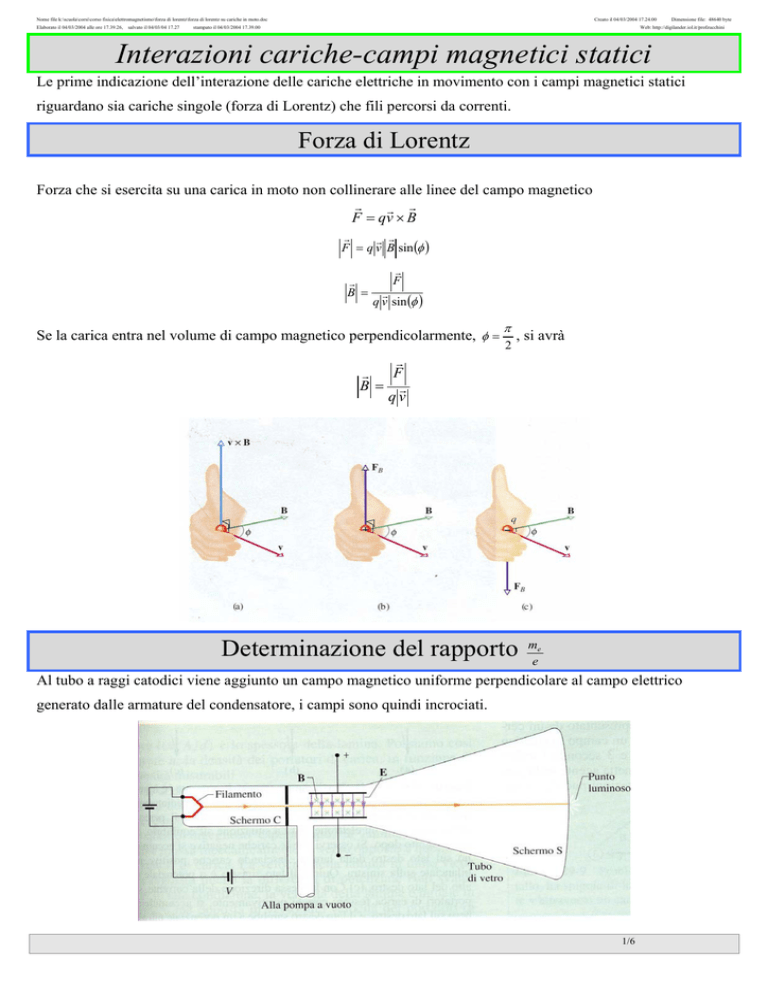
Forza che si esercita su una carica in moto non collinerare alle linee del campo magnetico
r
r r
F = qv × B
r
r r
F = q v B sin (φ )
r
B =
r
F
r
q v sin (φ )
Se la carica entra nel volume di campo magnetico perpendicolarmente, φ =
π
2
, si avrà
r
F
r
B= r
qv
Determinazione del rapporto
me
e
Al tubo a raggi catodici viene aggiunto un campo magnetico uniforme perpendicolare al campo elettrico
generato dalle armature del condensatore, i campi sono quindi incrociati.
1/6
Nome file k:\scuola\corsi\corso fisica\elettromagnetismo\forza di lorentz\forza di lorentz su cariche in moto.doc
Elaborato il 04/03/2004 alle ore 17.39.26, salvato il 04/03/04 17.27
Creato il 04/03/2004 17.24.00
stampato il 04/03/2004 17.39.00
Dimensione file: 48640 byte
Web: http://digilander.iol.it/profzucchini
Thomson utilizzò questo metodo per determinare il rapporto
me
e
La misura si compone di tre passi :
r
r
1. misuro la posizione del fascio non deflesso con E = 0 , B = 0
r
2. Applico il campo elettrico E ≠ 0 e misuro la deflessione del fascio
r
3. Applico il campo magnetico B ≠ 0 fino a riportare il il fascio nella posizione iniziale non deflessa
Al punto 2 avrò y =
Quando applico
r
e E L2
2me v 2
r
B≠0
avrò
r
r r
e E = ev B
da cui
r
r E
v = r
B
eEL2
y=
r
⎛E
⎜
2me ⎜ r
⎜B
⎝
r2
e B L2
=
r
2
2me E
⎞
⎟
⎟⎟
⎠
Da cui avrò
r2
B L2
me
=
r
e
2y E
Effetto Hall
Quando un conduttore viene immerso in un volume in cui è presente
campo magnetico si avrà una tendenza alla ridistribuzione delle cariche
con la creazione di una differenza di potenziale ortogonale allo scorrere
della corrente.
La figura mostra in a e b cosa accade se le particelle portatrici di carica
sono negative:
in a vengono deviate verso destra creandosi così una differenza di
potenziale fra i due lati del conduttore essendo positivo il lato sinistro e negativo conseguentemente il destro.
In b si crea un campo elettrico tale da contrastare la deflessione delle particelle e conseguentemente la corrente
riprende a scorrere regolarmente lasciando però la differenza i potenziale sui lati del conduttore.
Se i portatori fossero positivi, si avrebbe la situazione c con conseguente polarizzazione del conduttore opposta
al caso precedente.
La misura del potenziale ai lati del conduttore può dare indicazione delle cariche in movimento.
E’ possibile anche stimare la densità di portatori di carica:
r r
V = E d
All’equilibrio delle due forze elettrica e magnetica si avrà
2/6
Nome file k:\scuola\corsi\corso fisica\elettromagnetismo\forza di lorentz\forza di lorentz su cariche in moto.doc
Elaborato il 04/03/2004 alle ore 17.39.26, salvato il 04/03/04 17.27
Creato il 04/03/2004 17.24.00
stampato il 04/03/2004 17.39.00
r
r r
e E = e vd B
La densità di portatori di carica sarà
i = nvd eA
Da cui
r
i r
eE =e
B
neA
Da cui infine si avrà
r
r r
r
i B i B d
i B
n=
=
r =
eA E e V A e Vl
Essendo l lo spessore della lamina
Cariche in moto circolare
La forza di Lorentz essendo sempre ortogonale al piano
individuato da velocità e campo magnetico agisce curvando la
traiettoria delle particelle su percorsi circolari.
Le forze che si bilanciano saranno la forza di Lorentz e la forza
centripeta
r
r r
v2
F = qv × B = m
r
Da cui
r r
v2
q v B sin (φ ) = m
r
Ed infine si avrà il raggio di Larmor
rLarmor
Se φ =
π
2
r
mv
= r
q B sin (φ )
si ha
rLarmor
r
mv
= r
qB
Il periodo di rotazione sarà
r
2πrLarmor 2π m v
2πm
= r
T=
r = r
r
v
v qB
qB
La frequenza è
r
1 qB
ν= =
T 2πm
E la pulsazione sarà
ω = 2πν =
Dimensione file: 48640 byte
Web: http://digilander.iol.it/profzucchini
r
qB
m
3/6
Nome file k:\scuola\corsi\corso fisica\elettromagnetismo\forza di lorentz\forza di lorentz su cariche in moto.doc
Elaborato il 04/03/2004 alle ore 17.39.26, salvato il 04/03/04 17.27
Creato il 04/03/2004 17.24.00
stampato il 04/03/2004 17.39.00
Nel caso in cui l’angolo fra velocità delle particelle e campo magnetico sia φ =
Dimensione file: 48640 byte
Web: http://digilander.iol.it/profzucchini
π
2
si avrà che solo la proiezione
della velocità sulla direzione ortogonale al campo genererà il moto circolare delle particelle mentre nella
direzione delle linee del campo si avrà un moto rettilineo uniforme ottenendosi, componedo i due moto un
percorso elicoidale avvolto attorno alle linee del campo.
Quest’ultima immagine è molto importante e significativa: tutte le cariche elettriche se accelerate emettono
radiazione e gli elettroni che ruotano lingo le linee del campo magnetico non si sottraggono a questa regola
emettendo una radiazione chiamata radiazione di sincrotrone
4/6
Nome file k:\scuola\corsi\corso fisica\elettromagnetismo\forza di lorentz\forza di lorentz su cariche in moto.doc
Elaborato il 04/03/2004 alle ore 17.39.26, salvato il 04/03/04 17.27
Creato il 04/03/2004 17.24.00
stampato il 04/03/2004 17.39.00
Dimensione file: 48640 byte
Web: http://digilander.iol.it/profzucchini
Il Sincrotrone
Il ciclotrone è costituito da due cavitàa forma di D collegate ad un
generatore di tensione che inverte la polarità con un segnale di
frequenza ν osc del tipo V = V0 cos(2πν osc t ) .
Se la frequenza di rotazione delle particelle ν =
qB
1
=
T 2πm
coincide con
la frequenza ν osc ogni mezzo giro la carica si trova nel passaggio tra
le due intercapedini ad essere accelerata e quindi percorrerà ad ogni
mezzo giro un’arco di circonferenza più grande con maggiore
velocità ed energia.
Si avrà quindi
ν osc =
qB
2πm
Quando le carhc raggiungono orbite prossime alla periferia delle cavità,
una placca di deflessione opportuna fa sì che possano “sfuggire” per la
tangente costituendo un fascio di particelle molto energetiche.
Per cariche di grande energia gli effetti relativistici portano ad una
complicazione del problema e non è più sufficiente intervenire solo sulla
polarità delle due cavità ma si deve variare sia la frequenza ν osc che il
r
campo magnetico B ; in questo modo le particelle accelerate non variano più il loro raggio ma percorrono orbite
a raggio costante ma sempre a velocità superiori senza però ai raggiungere la velocità c.
5/6
Nome file k:\scuola\corsi\corso fisica\elettromagnetismo\forza di lorentz\forza di lorentz su cariche in moto.doc
Elaborato il 04/03/2004 alle ore 17.39.26, salvato il 04/03/04 17.27
Creato il 04/03/2004 17.24.00
stampato il 04/03/2004 17.39.00
Dimensione file: 48640 byte
Web: http://digilander.iol.it/profzucchini
6/6