Nome file k:\scuola\corsi\corso fisica\elettromagnetismo\forza di lorentz\forza di lorentz su conduttori percorsi da corrente.doc
Elaborato il 04/03/2004 alle ore 17.31.01, salvato il 04/03/04 17.30
Creato il 19/02/2004 8.43.00
stampato il 04/03/2004 17.31.00
Dimensione file: 48640 byte
Web: http://digilander.iol.it/profzucchini
Interazioni cariche-campi magnetici statici
Quando le cariche si muovono all’interno di un conduttore posto in una zona di campo magnetico e quando il
conduttore non è disposto nella direzione del campo, il filo risente di una forza dovuta all’efetto collettivo delle
cariche interne al conduttore.
Forza di Lorentz su conduttori percorsi da corrente
immersi in un campo magnetico
Abbiamo visto che la singola carica interagisce con il campo
magnetico.
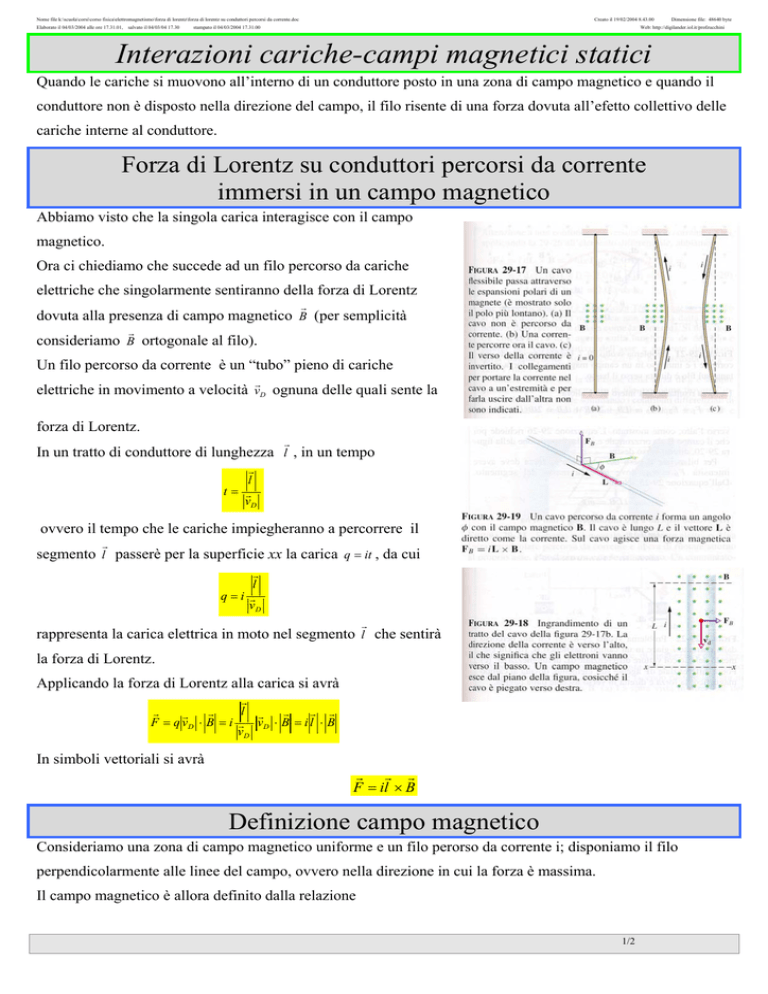
Ora ci chiediamo che succede ad un filo percorso da cariche
elettriche che singolarmente sentiranno della forza di Lorentz
r
dovuta alla presenza di campo magnetico B (per semplicità
r
consideriamo B ortogonale al filo).
Un filo percorso da corrente è un “tubo” pieno di cariche
r
elettriche in movimento a velocità vD ognuna delle quali sente la
forza di Lorentz.
r
In un tratto di conduttore di lunghezza l , in un tempo
r
l
t= r
vD
ovvero il tempo che le cariche impiegheranno a percorrere il
r
segmento l passerè per la superficie xx la carica q = it , da cui
r
l
q=i r
vD
r
rappresenta la carica elettrica in moto nel segmento l che sentirà
la forza di Lorentz.
Applicando la forza di Lorentz alla carica si avrà
r
l r
r r
r
r
r
r
F = q vD ⋅ B = i r vD ⋅ B = i l ⋅ B
vD
In simboli vettoriali si avrà
r r r
F = il × B
Definizione campo magnetico
Consideriamo una zona di campo magnetico uniforme e un filo perorso da corrente i; disponiamo il filo
perpendicolarmente alle linee del campo, ovvero nella direzione in cui la forza è massima.
Il campo magnetico è allora definito dalla relazione
1/2
Nome file k:\scuola\corsi\corso fisica\elettromagnetismo\forza di lorentz\forza di lorentz su conduttori percorsi da corrente.doc
Elaborato il 04/03/2004 alle ore 17.31.01, salvato il 04/03/04 17.30
Creato il 19/02/2004 8.43.00
stampato il 04/03/2004 17.31.00
Dimensione file: 48640 byte
Web: http://digilander.iol.it/profzucchini
F
il
B=
L’unità di misura del sistema internazionale è il Tesla
1T =
1N
1 A ⋅1 m
Equazione generale per la forza su un filo percorso da corrente
immerso in campo magnetico
Nel caso in cui la disposizione relativa filo-campo vari lungo il filo, è necessario calcolare la forza complessiva
come il contributo di tutte le forze infinitesime su porzioni infinitesime di filo e sommate integralmente.
La Precedente relazione sarà allora
r r
r
dF = idl × B
E il calcolo della forza complessiva sarà
r
r
F = ∫ dF
l
Calcoliamo la forza sentita dalla spira a fianco, percorsa da corrente i in una zona di campo magnetico
ortogonale al piano della spira.
La parte rilevante del problema è il calcolo del contributo
della semicirconferenza alla forza complessiva.
r
r
r
Ogni elemento infinitesimo darà un contributo dF = i B dl
ortogonalmente alla spira, ma scomponendo si avrà un
contributo ortogonale al diametro indicato ed uno parallelo.
Quelli paralleli al diametro si elidono mentre quelli ortogonali
si sommano.
L’arco di semicirconferenza può essere descritto utilizzando l’angolo θ
r
dl = Rdθ
Per avere questi ultimi si avrà
r
r
dF = i B sin (θ )Rdθ
r
r
r
r
r
r
π
Fl = ∫ i B sin (θ )Rdθ = i B R ∫ sin (θ )dθ = i B R[− cos(θ )]0 = i B R[1 + 1] = i B 2 R
l
l
Il contributo della semicirconferenza alla forza agente sul conduttore è quindi equivalente a quello di un
conduttore rettilineo collineare alle porzioni di filo ai lati della semicirconferenza, di lunghezza pari al
diametro.
2/2












