elementi di termodinamica - Arch

Corso di Fisica tecnica e ambientale – a.a. 2011/2012 - Docente: Prof. Carlo Isetti
CAPITOLO 7B
ELEMENTI DI TERMODINAMICA
7.1 PROPRIETÀ DI UNA SOSTANZA PURA
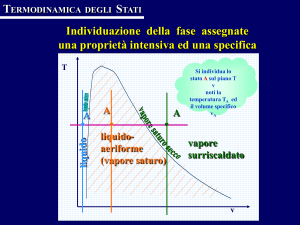
Come si ricorderà, lo stato termodinamico di una sostanza pura chimicamente definita
è individuato dai valori assunti da due grandezze di stato intensive ed indipendenti tra loro. In
tali condizioni, anche il valore assunto da qualsivoglia altra variabile termodinamica risulta
definito. Si è già anche detto che l'equazione di stato del gas ideale Pv = RiT costituisce
spesso un'ottima approssimazione del comportamento di tutte le sostanze allo stato aeriforme
purché queste si trovino in condizioni di sufficiente rarefazione (elevati valori del volume
specifico). In pratica, queste condizioni si verificano in corrispondenza a pressioni
sufficientemente basse e/o a temperature sufficientemente elevate. Quando si prendono in
considerazioni condizioni via via sempre meno "rarefatte", cominciano a verificarsi, dapprima
variazioni significative dal comportamento ideale e, successivamente, anche altri vistosi
cambiamenti, ad esempio il fluido, da aeriforme, diventa liquido, e da liquido, solido. Questi
fenomeni sono conseguenti al manifestarsi di forze attrattive tra le molecole del fluido, via via
sempre più intense, man mano che queste si accostano le une alle altre.
In generale, in queste condizioni, non è possibile stabilire un'equazione di stato che
rappresenti i possibili stati del fluido, per cui si ricorre alla determinazione sperimentale
diretta delle grandezze di stato esprimendo i valori contenuti in forma grafica (diagramma di
stato) o di tabelle di valori. Ad esempio si possono misurare i valori assunti dal volume
specifico v al variare della pressione P, mantenendo costante la temperatura t del sistema.
A questo scopo, si consideri l’acqua contenuta in un cilindro di vetro fornito di uno stantuffo
mobile come rappresentato in figura. Si supponga che il cilindro contenga esattamente una
massa m = 1 [kg].
CAPITOLO 7B
Elementi di termodinamica
Corso di Fisica Tecnica – a.a. 2010/2011 - Docente: Prof. Carlo Isetti
Lo stato iniziale del fluido è individuato dai valori della pressione P1 pari alla pressione
ambiente e dal valore della temperatura t1, pari alla temperatura ambiente (stato 1).
Il volume occupato dal fluido può essere facilmente misurato; esso risulta: v1  10-3 [m3/kg].
Si supponga ora di portare il fluido in uno stato diverso, 1°, caratterizzato da P1° = 2
P1 e t1°= t1 . In questo stato risulta v1° v1 e cioè l'acqua liquida risulta praticamente
incomprimibile. In figura gli stati 1 e 1° sono rappresentati in un diagramma (P,v). Il tratto di
isoterma che li unisce risulta praticamente verticale.
Si consideri nuovamente il sistema nello stato 1 e si supponga ora, mantenendo
costante la pressione P1 di fornire al fluido la quantità di calore Q1,2 > 0, incrementando così
la temperatura dello stesso fino al valore t2 > t1 come previsto dalla relazione:
Q1,2 = c (t2 - t1).
In questo stato il volume specifico dell'acqua v2 risulta leggermente maggiore di v1. Se ora, a
partire dallo stato 2, portiamo nuovamente la pressione al valore P2° = 2P2 = 2P1, a
temperatura t2 = cost., si avrà, analogamente a prima una trasformazione a tratto verticale
(trasformazione 22° in figura).
In definitiva, per acqua allo stato liquido, tutte le isoterme sul piano (p,v) presentano un
andamento praticamente verticale. Riportato ora il sistema alla pressione P2 = P1 = cost., si
può continuare a fornire calore al fluido, a pressione costante, al fine di aumentare la sua
temperatura. Ebbene, l'acqua aumenta la sua temperatura fino a raggiungere t3= 100 [°C],
quando avviene un fatto inaspettato: inizia a formarsi una fase aeriforme e cioè la prima bolla
di vapore. In queste condizioni si dice che il sistema ha raggiunto uno stato limite (stato 3: t3
= 100 [°C], P3 = P1, v3 > v2) detto liquido saturo. Se, analogamente a prima, a partire dallo
stato 3, portiamo la pressione al valore P3° = 2P3, a temperatura t3= cost., si otterrà la
trasformazione isoterma 33° che risulta, analogamente a prima, praticamente verticale (vedi
figura).
CAPITOLO 7B
Elementi di termodinamica
Corso di Fisica Tecnica – a.a. 2010/2011 - Docente: Prof. Carlo Isetti
Se si fornisce ancora calore all'acqua, mantenendo costante la pressione, la fase
liquida si trasforma con continuità in vapore, mantenendo costante la temperatura t3 fino a
che si giunge ad uno stato 4, in cui tutto il liquido si è trasformato in vapore (P4 = P3 = P1 , t4
= t3 = 100 [°C], v4 » v3). Lo stato 4 viene detto vapore saturo secco.
Questo processo, tra gli stati 3 e 4, detto di vaporizzazione, risulta quindi,
contemporaneamente, isobaro ed isotermo. Durante la vaporizzazione, il volume specifico
del sistema, aumenta in modo notevolissimo (circa 1000 volte). Durante questo processo, si
noti, il calore specifico dell’acqua può considerarsi infinito.
La quantità di calore necessaria a realizzare un siffatto processo viene detta calore
latente di vaporizzazione r [kJ/kg]. Essendo il processo isobaro risulta anche:
r = h4 - h3
e cioè la quantità di calore necessario è pari alla variazione di entalpia del sistema tra i due
stati di vapore saturo secco (4) e lo stato di liquido saturo (3).
In ogni punto, durante il processo di vaporizzazione 3-4, si ha la contemporanea presenza di
liquido e vapore; il volume specifico del liquido durante il processo di vaporizzazione è
sempre v3 , mentre quello del vapore in equilibrio è sempre v4. Il volume specifico dell'intero
sistema risulta variare tra i due limiti suddetti in dipendenza delle rispettive quantità di
liquido e di vapore.
Se si fornisce, sempre mantenendo costante la pressione, ulteriore calore al sistema,
ormai formato dalla sola fase vapore (stato 4), la temperatura aumenta di nuovo. Ad esempio,
in uno stato 5 (P5 = P4 , v5>v4), risulta t5 > t4.
Per individuare l'andamento dell'isoterma t3 = t4 a destra dello stato 4, si può portare il
sistema in uno stato 6 per cui risulti t6 = t4 e v6 > v4 .
Come rappresentato in figura risulta P6 < P4 . Se si ripete questa procedura per valori
crescenti della pressione si può costruire il diagramma (diagramma della sostanza pura acqua)
riportato qualitativamente nella seguente figura.
CAPITOLO 7B
Elementi di termodinamica
Corso di Fisica Tecnica – a.a. 2010/2011 - Docente: Prof. Carlo Isetti
Si osserva che: i luoghi dei punti di inizio e di fine vaporizzazione, definiscono due
curve limite che si incontrano in un punto C, detto punto critico. La zona al di sotto di queste
due curve è la zona del vapore saturo definito come condizione nella quale coesistono in
condizioni di equilibrio liquido e vapore.
La curva limite a sinistra viene detta curva limite inferiore e rappresenta le condizioni di
liquido saturo: a destra si ha contemporanea presenza di liquido e vapore, a sinistra presenza
di solo liquido; l'altra, curva limite superiore, rappresenta lo stato di vapore saturo secco: a
sinistra si ha ancora presenza di liquido e vapore, mentre a destra si ha solo vapore, che viene
detto vapore surriscaldato.
Nel diagramma rappresentato in figura si possono ancora osservare le seguenti caratteristiche:
a)
esiste un'isoterma critica tc, caratteristica di ogni sostanza, al di sopra della quale,
qualunque sia la pressione ed il volume, il sistema è sempre allo stato aeriforme (regione
del gas), in questa regione, se si considera il gas perfetto, le isoterme si presentano con
CAPITOLO 7B
Elementi di termodinamica
Corso di Fisica Tecnica – a.a. 2010/2011 - Docente: Prof. Carlo Isetti
un andamento di iperbole equilatera, secondo quanto deriva dall'equazione di stato dei
gas perfetti;
b)
al di sotto della temperatura critica ed a destra della curva limite superiore, il sistema è
ancora nella fase aeriforme; l'andamento di un'isoterma è abbastanza simile a quello
dell'isoterma di un gas perfetto; si osservi che però è sufficiente aumentare la pressione,
a T costante, perché abbia inizio la condensazione (regione del vapore surriscaldato);
c)
al di sotto della temperatura critica ed all'interno delle curve limite, il sistema è in parte
nella fase vapore ed in parte nella fase liquida, in questa zona è possibile variare il
volume del vapore saturo senza variare la sua pressione; il comportamento del vapore
saturo è quindi profondamente diverso da quello di un gas (come già accennato, questa è
definita come regione del vapor saturo);
d)
la regione al di sotto della temperatura critica ed a sinistra della curva limite inferiore è
detta regione del liquido; l'andamento quasi verticale delle isoterme corrisponde al fatto
che la fase liquida è praticamente incomprimibile;
e)
nella regione del vapore saturo lo stato del sistema non può ovviamente essere
individuato in base ai valori assunti dalla coppia di variabili P e t in quanto esse, in questa
regione del diagramma, non sono grandezze tra loro indipendenti essendo in condizioni di
saturazione (pedice s) Ps= f(ts); in tale situazione lo stato del sistema potrà invece, ad
esempio, essere individuato dalla coppia di variabili indipendenti (P,v).
Si ricorda che il calore (latente) di vaporizzazione r (kJ/kg) rappresenta la quantità di
calore necessaria perchè l’unità di massa di liquido saturo si porti nello stato di vapore
saturo secco. La stessa quantità di calore deve essere sottratta al sistema nello stato di vapore
saturo secco per condensare e raggiungere lo stato di liquido saturo.
Si osservi sul diagramma come al crescere della pressione il processo di vaporizzazione e
quindi di trasformazione tra lo stato di liquido saturo a vapore saturo secco avvenga a
temperature sempre più elevate. Per una sostanza pura esiste una relazione ben definita tra la
pressione di saturazione Ps e la corrispondente temperatura di saturazione ts; per l’acqua essa
può essere rappresentata dalla seguente espressione:
Ps  610.5 e
17.269 t S
237.3  t S
(valida per temperature ts  0 [°C])
Per l'acqua a pressione ambiente (Pa= 101300 [Pa]), il processo di vaporizzazione
inizia quando Ps = Pa e ts = 100 [°C].
CAPITOLO 7B
Elementi di termodinamica
Corso di Fisica Tecnica – a.a. 2010/2011 - Docente: Prof. Carlo Isetti
In figura è riportato qualitativamente l'andamento della funzione Ps = f(ts).
7.2 SECONDO PRINCIPIO DELLA TERMODINAMICA
Sulla base del primo principio della termodinamica si è visto come scambi di calore e
lavoro, sebbene qualitativamente differenti, siano quantitativamente equivalenti, ad esempio,
per determinare la complessiva variazione di energia interna di un sistema in un generico
processo 12:
Q1,2 - L1,2 = u2 - u1
Sempre in base al I° Principio, scambi di calore e lavoro sono entrambi forme di energia. Si
consideri, ad esempio, un processo isotermo di espansione di un gas ideale (v2-v1 > 0), e cioè
un processo 12 caratterizzato da du = 0 e quindi da u2 - u1 = 0;
ebbene, risulta:
Q1,2 = L1,2
e, cioè, il sistema può compiere, durante questo processo, un lavoro L1,2 > 0 equivalente al
calore fornito al sistema Q1,2 > 0. Questo processo può essere realizzato senza nessuna
difficoltà. Si noti però come lo stato finale del sistema (2) sia diverso dallo stato iniziale.
Pertanto, se il nostro scopo è realizzare processi termodinamici che consentano di ottenere
con continuità lavoro meccanico a spese di scambi di calore col sistema, sarà
evidentemente necessario prendere in considerazione unicamente processi al termine dei
quali il sistema riassuma lo stesso stato termodinamico e cioè processi ciclici. Solo
processi ciclici potranno essere ripetuti senza alcuna limitazione in macchine termiche.
Si consideri ora il caso di un processo ciclico (stato 2 = stato 1) per il quale risulta
complessivamente u2 = u1 e quindi Q1,2 = L1,2; ebbene parrebbe ancora del tutto indifferente
convertire la forma di energia "lavoro" nella forma "calore" oppure realizzare il processo
opposto.
Si consideri il dispositivo rappresentato in figura a lato,. A tale
dispositivo, alla variazione di quota della massa m, viene fornita
al sistema (ad esempio acqua) una quantità di lavoro L < 0 (pari
alla variazione di energia potenziale gravitazionale -m*gh).
CAPITOLO 7B
Elementi di termodinamica
Corso di Fisica Tecnica – a.a. 2010/2011 - Docente: Prof. Carlo Isetti
In una prima fase, come conseguenza dello scambio di lavoro, la temperatura dell'acqua
aumenta mentre in una seconda il sistema scambia calore con l'ambiente esterno a
temperatura T. Alla fine di questo processo, e cioè, all'equilibrio termico con l'ambiente,
l’acqua è ritornata nello stato iniziale (u = 0). Una quantità di calore Q = L < 0 è stata
ceduta all'ambiente circostante il quale, con ottima approssimazione, durante questo processo
può sempre considerarsi alla temperatura costante T. L'ambiente può essere, infatti
,considerato una sorgente termica, e cioè come un grande serbatoio termico capace di fornire
ed assorbire calore mantenendo inalterata la sua temperatura.
Questo ed altri simili processi ciclici, che vedono lavoro L fornito ad un sistema
integralmente ritrovarsi in calore Q ceduto ad una sorgente esterna (si dice anche scambiando
calore con una sola sorgente termica) sono realizzabili. In questi processi risulta verificato il
seguente criterio:
Q
Q
 Ti  T  0
i
L'esperienza insegna però che il processo ciclico descritto non può essere invertito: in altre
parole è impossibile sollevare una massa m grazie a del lavoro L > 0 fornito da un sistema
con cui si scambi Q > 0 con la sorgente termica (ad esempio l’ambiente circostante).
Quest'ultimo processo, impossibile a realizzarsi, richiederebbe :
Q
Q
 Ti  T  0
i
La constatazione che il processo ciclico appena considerato può evolvere solo nel senso per
cui è Q < 0 e L < 0 e non al contrario (Q > 0, L > 0) costituisce l'essenza del II° Principio
della Termodinamica, che può essere così enunciato:
"è impossibile realizzare un processo ciclico in cui un sistema chiuso produca lavoro
motore (L > 0) scambiando calore con una sola sorgente termica".
Per ottenere lavoro motore occorre, quindi, scambiare calore con almeno due sorgenti a
temperature diverse. L'esperienza mostra che ogni processo ciclico che fornisca con
continuità lavoro a spese di scambi di calore rispetta sempre il criterio prima ricordato:
Q
 Ti  0
i
Il criterio può anche essere espresso nella forma:
dQ
 T 0
Se si opera poi in modo opportuno al fine di ridurre attriti e cause di irreversibilità, si osserva
che:

dQ
0
T
CAPITOLO 7B
Elementi di termodinamica
Corso di Fisica Tecnica – a.a. 2010/2011 - Docente: Prof. Carlo Isetti
Una formulazione più generale del secondo principio (relazione di Clausius) è
sintetizzata dall'espressione:
dQ
 T 0
il segno di uguaglianza vale per condizioni di reversibilità per cui nel caso si consideri un
processo ciclico reversibile si può quindi scrivere:
dQ
 Trev  0
Questa condizione matematica, come già precedentemente osservato, comporta l'esistenza di
una funzione di stato detta entropia (simbolo S) il cui differenziale dS vale:
dS 
dQ rev
T
Risulta quindi che, in condizioni di reversibilità, la variazione di entropia dS in un processo
elementare è solo dovuta al verificarsi dello scambio di calore dQrev .
Nel caso, invece, che il suddetto processo elementare non sia reversibile, sempre
risulta dS > dQ/T, ove dQ rappresenta lo scambio effettivo di calore; in altre parole la
variazione di entropia dS è determinata solo in parte dallo scambio termico dQ.
In tutta generalità si usa scrivere:
dS 
dQ
 dS s
T
ove con l'introduzione del termine dSs > 0 si vuol esprimere l'effetto provocato dalle cause di
irreversibilità.
Un processo elementare spontaneo e, pertanto, irreversibile comporterà dSs > 0.
Nell'ipotesi che questo processo fosse adiabatico, la variazione di entropia del sistema
risulterebbe sempre positiva (dS = dSs > 0 essendo dQ = 0); mentre nel caso di processo
adiabatico reversibile risulterebbe ovviamente dS = 0. La variazione di entropia conseguente
ad una trasformazione tra uno stato iniziale 1 e finale 2, può essere calcolata mediante
l'espressione:
2
dQ rev
S 2  S1  
T
1
2
si noti che S2 - S1 è, per una trasformazione non reversibile, diverso da

1
dQ
.
T
In altre parole, la variazione di entropia S tra uno stato e l'altro può essere calcolata
immaginando una qualsiasi successione di trasformazioni reversibili che a partire dallo stato
iniziale porti a quello finale, e valutando per ciascuna trasformazione la variazione relativa di
dQ rev
entropia S mediante l'espressione 
.
T
CAPITOLO 7B
Elementi di termodinamica
Corso di Fisica Tecnica – a.a. 2010/2011 - Docente: Prof. Carlo Isetti
Si consideri ora un sistema termicamente isolato (dQ = 0). Sulla base delle relazioni
precedentemente discusse, si può osservare che il sistema può evolvere spontaneamente solo
nel senso in cui è dS = dSs > 0 ossia nel senso in cui la sua entropia aumenta. L'evoluzione
spontanea del sistema continua fino a che non risulta dS = dSs = 0, e cioè quando la sua
entropia non ha raggiunto il valore massimo compatibile con i vincoli cui è soggetto il
sistema. Solo in questo stato il sistema ha raggiunto una definitiva condizione di equilibrio.
Si consideri il sistema isolato rappresentato in figura ove, ad un certo istante, risultino
presenti i corpi 1 e 2, rispettivamente a temperature T1 e T2. Sulla base di quanto detto, il
sistema potrà evolvere solo nel senso in cui dS > 0. Se si indica con dQ1 la quantità di calore
scambiata dal corpo 1 col corpo 2 nel corso di un processo reversibile equivalente al
processo spontaneo la complessiva variazione di entropia del sistema deve risultare:
dS = dS1 + dS2 = dQ1 /T1 + dQ2 /T2 > 0
ove: dQ1 rappresenta la quantità di calore scambiata dal corpo 1.
Ponendo dQ1 = - dQ2 si ottiene infine:
dS = dS1 + dS2 = dQ1 (T2 - T1 )/T1 T2 > 0
La condizione dS > 0 comporta che sia dQ1 > 0 e T2 > T1 oppure dQ1 < 0 e T2 < T1, e
cioè che il calore passi spontaneamente da corpi a temperatura più elevata verso quelli a
temperatura inferiore. L'evoluzione del sistema procede fino a quando la sua entropia non
raggiunge il suo valore massimo finale Sf e cioè fino alla condizione di equilibrio termico.
La condizione dS = 0 richiede, come immediatamente si osserva, che nella situazione finale
di equilibrio le temperature dei due corpi siano eguali.
SITUAZIONE INIZIALE
T1>T2
Si = M1 s1 + M2 s2
SITUAZIONE FINALE
aumenta fino a
T1* = T2*
Sf = M1 s1* + M2 s2*
Con il simbolo s [kJ/kg K], si è indicata l'entropia specifica riferita cioè all'unità di massa.
Raggiunta questa situazione di equilibrio, l'entropia ha raggiunto il suo massimo valore Sf e in
queste condizioni è T1* = T2*.
CAPITOLO 7B
Elementi di termodinamica
Corso di Fisica Tecnica – a.a. 2010/2011 - Docente: Prof. Carlo Isetti
7.3 UN PROCESSO CICLICO IDEALE: LA MACCHINA TERMICA DI CARNOT
Si può dire in generale che in un sistema isolato il calore passa spontaneamente da
corpi a temperatura più elevata verso quelli a temperatura inferiore. Il processo inverso non
può avvenire spontaneamente ma richiede consumo di lavoro meccanico fornito dall'esterno.
Si consideri il sistema operante secondo un processo ciclico (macchina termica)
rappresentato schematicamente nella figura seguente. Ad ogni ciclo la macchina produce
lavoro utile scambiando calore con due sorgenti a diversa temperatura. Ripetendo
successivamente il ciclo, sarà possibile ottenere con continuità lavoro meccanico a spese di
energia termica.
Se si suppone il ciclo reversibile, risulta:

dQ
0
T

Q1 Q 2

0
T1
T2
poiché viene fornito calore alla temperatura T1 al sistema, è:
Q1
0
T1
e, quindi, deve essere:
Q2
0
T2
Il lavoro ottenibile, quindi, da una macchina termica è sempre minore dell'energia termica
fornita Q1 perchè una certa quota (Q2 < 0) deve essere ceduta alla sorgente termica alla
temperatura minore T2 (in genere, è disponibile, come sorgente, l’ambiente esterno).
Si può definire un rendimento di conversione  come rapporto tra il lavoro utile
fornito dal ciclo L e l'energia termica Q1fornita al fluido operante nel ciclo:
CAPITOLO 7B
Elementi di termodinamica
Corso di Fisica Tecnica – a.a. 2010/2011 - Docente: Prof. Carlo Isetti
 = L / Q1
essendo in un processo ciclico sempre L = Q1+ Q2, risulta:
 = 1 + Q2/Q1
Nel caso di reversibilità, tenendo conto dell' enunciato di Clausius, si ha:
Q1 Q 2

0
T1
T2
e, quindi, risulta:
o =  = 1 - T2 / T1
Si osservi che in questo caso o è solo funzione delle temperature assolute delle
sorgenti termiche T1 e T2, ed è indipendente quindi dalla natura del fluido operante della
macchina. Il rendimento di conversione o risulta tanto più elevato quanto più elevata è la
temperatura della sorgente che fornisce calore T1 e bassa la temperatura della sorgente che
assorbe calore T2. Poiché ovviamente la temperatura inferiore T2 è determinata dalla
temperatura dell'ambiente esterno, che costituisce la sorgente termica in cui viene a scaricarsi
la quantità di calore Q2, l'unico modo di aumentare o consiste nell' aumentare T1 .
Si può dimostrare che nessuna macchina termica operante tra due sole sorgenti, può
essere caratterizzata da  > o. Questo processo ciclico è detto ciclo di Carnot: le
trasformazioni termodinamiche lungo le quali avvengono gli scambi Q1 e Q2 sono isoterme,
mentre le due altre trasformazioni necessarie per chiudere il ciclo sono adiabatiche.
Nella figura seguente è rappresentato tale ciclo per un gas perfetto.
Trasformazione AB
T1 = cost.
Q1 = Ri T1 ln vB / vA > 0
Trasformazione CD T2 = cost.
Q2 = Ri T2 ln vD / vC < 0
CAPITOLO 7B
Elementi di termodinamica
Corso di Fisica Tecnica – a.a. 2010/2011 - Docente: Prof. Carlo Isetti
Per le trasformazioni adiabatiche reversibili BC e DA, valgono le relazioni:
PB vBk = PC vCk
e
PD vDk = PC vCk
è facile dimostrare che:
vB / vA = vD / vC
per cui:
o = 1 + Q2 / Q1 = 1 - T2 / T1
Il ciclo sopra descritto può essere anche rappresentato in un diagramma avente come
coordinate le grandezze di stato T ed S (diagramma entropico).
Risulta immediatamente:
B

trasformazione AB (isoterma): T1 = cost ;
Q 1   T ds  T1 s B  s A   0
A

trasformazione BC (adiabatica reversibile):
dQrev= 0
ds = dQrev / T = 0
D

trasformazione CD (isoterma): T2 = cost.
Q 2   T ds  T2 s D  s C   0
C

trasformazione DA (adiabatica reversibile):
dQrev= 0
ds = dQrev / T = 0
Nel caso, poi in cui il ciclo suddetto non sia composto da trasformazioni tutte reversibili, si
avrà:
Q 1' Q '2

0
T1
T2
ove con Q'1 e Q'2 si sono indicati i relativi scambi. Se si effettua un confronto tra i due casi si
osserva che, parità di calore fornito Q'1 = Q1, la quota ceduta all'ambiente Q'2 risulta (in
valore assoluto) maggiore di Q2. Il lavoro ottenuto L' è, pertanto, minore:
L' = Q1 + Q'2 < L
' < o
CAPITOLO 7B
Elementi di termodinamica
Corso di Fisica Tecnica – a.a. 2010/2011 - Docente: Prof. Carlo Isetti
I cicli motori reali poi effettivamente realizzati (macchine termiche) sono
caratterizzati, oltre che dalla presenza di fenomeni di irreversibilità, anche da una molteplicità
di scambi di calore, con un gran numero di sorgenti termiche operanti a temperature diverse.
Si può dimostrare che in questi casi il rendimento è minore di quello ottenibile da una
macchina termica che operasse tra due sole sorgenti alle temperature estreme del ciclo.
A titolo di informazione, si riporta che in un motore a combustione interna si realizza
approssimativamente  = 0,33.
Ciò significa che, dell'energia termica prodotta dalla combustione del carburante, solo
un terzo circa viene convertito in lavoro meccanico; la rimanente parte viene quasi totalmente
ceduta all'ambiente attraverso i fumi di scarico e mediante il raffreddamento del liquido
circolante nel radiatore.
Nelle centrali termoelettriche, dove viene prodotta energia elettrica a spese di energia
termica, ottenuta a sua volta mediante processi di combustione o di fissione nucleare, il
rendimento di conversione realizzato è circa = 0,40. Ciò significa che circa il 60 %
dell'energia termica impiegata per la produzione di energia elettrica viene ceduta all'ambiente.
7.4 CENNI SUI CICLI FRIGORIGENI
In molte applicazioni, ad esempio per il condizionamento dell'aria, è necessario
ricorrere all'uso di macchine frigorigene per trasferire calore da un ambiente (un corpo, una
corrente d'aria etc.) a temperatura più bassa ad un altro ambiente (un altro corpo, un'altra
corrente d'aria etc.) a temperatura più elevata.
Da un punto di vista generale, oltre alla climatizzione di ambienti (condizionamento
dell'aria), la produzione del "freddo" presenta enorme importanza tecnica in molti altri settori,
ad esempio per la conservazione di prodotti deperibili, derrate alimentari, etc.
Sempre in accordo con il secondo principio, si può pensare di invertire il senso di
percorrenza del ciclo prima esposto, realizzando quindi un ciclo detto "inverso" o "frigo",
come rappresentato in figura.
CAPITOLO 7B
Elementi di termodinamica
Corso di Fisica Tecnica – a.a. 2010/2011 - Docente: Prof. Carlo Isetti
In questo ciclo una certa quantità di lavoro L < 0 viene compiuto sul sistema (macchina
frigorifera) il quale scambia una quantità di calore Q2 > 0 con la sorgente alla temperatura
minore T2. Una quantità di calore Q1 = (- Q2 + L) < 0 viene, invece, ceduta alla temperatura
più elevata T1.
In figura è rappresentato un ciclo inverso di Carnot sul diagramma termodinamico (T, S) per
un gas ideale.
Un ciclo inverso potrebbe, come già accennato, servire per due scopi distinti:
 sottrarre calore da un ambiente il quale deve essere mantenuto a temperatura più bassa
della temperatura circostante;
 somministrare calore a un ambiente che debba essere mantenuto a temperatura più elevata
della temperatura circostante.
Quando l'effetto desiderato consiste nella sottrazione di calore dalla sorgente a temperatura
più bassa Q2, si parla, come già detto, di macchina frigorigena; quando, invece, viene inteso
come effetto utile la fornitura della quantità di calore Q1 alla sorgente a temperatura più
elevata, si parla di pompa di calore.
Anche se dal punto di vista termodinamico il ciclo è il medesimo una pompa di calore
può, ad esempio, essere utilizzata per riscaldare un edificio (effetto utile Q1=- Q2 + L)
sottraendo calore Q2 all'ambiente esterno e consumando lavoro L.
Nell' ipotesi di un ciclo inverso di Carnot operante tra le due temperature T1 e T2,
come già osservato, risulta in base al secondo principio:
Q1 Q 2
Q1
T

0 
 1
T1
T2
Q2
T2
Se tale ciclo opera come ciclo frigo e cioè allo scopo di sottrarre calore alla sorgente
"fredda" si usa definire effetto utile COPf (coefficient of performance) il rapporto tra il
calore sottratto alla sorgente fredda - Q2 ed il lavoro consumato nel ciclo frigo L.
COPf è definito positivo essendo - Q2 < 0 ed L = Q1 + Q2 < 0:
COPf 
 Q2
 Q2
T2
1
1




L
Q1  Q 2
1  Q1 / Q 2
1  T1 / T2 T1  T2
CAPITOLO 7B
Elementi di termodinamica
Corso di Fisica Tecnica – a.a. 2010/2011 - Docente: Prof. Carlo Isetti
Nel caso, invece, in cui il ciclo operasse come pompo di calore viene definito l'effetto
utile COPp il rapporto tra il calore ceduto dal ciclo frigo alla sorgente "calda" Q1 ed il lavoro
consumato L. Il COPp è definito positivo essendo Q1 < 0 e L = Q1 + Q2 < 0.
Si ottiene:
Q
L  Q2
Q
T1
COPp  1 
 1  2  1  COPf 
L
L
L
T1  T2
Nei cicli inversi effettivamente adottati si possono realizzare effetti utili notevolmente
inferiori ad un ciclo inverso di Carnot; ad esempio nel caso di un ciclo frigo di Carnot
operante tra T1 = 303 [K] e T2 = 258 [K] rispettivamente 30 [°C] e -15 [°C] si ottiene un
valore del COPf = 5,74 mentre nella pratica si realizzano effetti utili fino al 50% inferiori.
In generale, anche se è possibile realizzare cicli inversi che utilizzino come fluido di
lavoro dei gas, è più opportuno, dal punto di vista tecnico, l'uso di particolari sostanze dette
freons (chimicamente derivate da idrocarburi ed in particolare idrocarburi alogenati, ad
esempio, il freon R12 o CCl2F2 diclorodifluorometano, il freon R11 o CCl3F
triclorofluorometano etc. Questi fluidi che alle temperature di lavoro subiscano passaggi di
fase liquido-vapore e vapore-liquido presentano favorevoli proprietà fisiche e
termodinamiche. In un primo processo il fluido di lavoro vaporizza (T e P costanti) sottraendo
calore alla sorgente inferiore mentre successivamente condensa a temperatura e pressione più
alta cedendo calore all’esterno. Il ciclo lavora pertanto tra due ben distinti livelli di pressione.
È opportuno ricordare che attualmente in tutto il mondo si stanno attivamente
cercando fluidi termodinamici alternativi ai freons. Queste sostanze infatti che,
inevitabilmente si troveranno ad essere immessi nell'atmosfera, sono in grado di determinare
una riduzione dello strato di ozono (O3) presente nell'alta atmosfera terrestre in misura
dipendente dalla loro specifica natura chimica. Come noto, lo strato di ozono adempie
all'importante funzione di assorbire efficacemente parte delle radiazioni solari ultraviolette
più energetiche e pertanto più dannose.
A parte questi aspetti, si può osservare che, se si cercasse di realizzare un ciclo inverso
di Carnot nella zona del vapore saturo, come ad esempio, rappresentato sul diagramma T, S
(le curve limiti che delimitano la zona di equilibrio tra liquido e vapore, corrispondono alle
ben note curve limiti del diagramma P, v), si dovrebbero realizzare trasformazioni di
compressione ed espansione adiabatiche di un vapore saturo (e, cioè, contenente goccioline di
liquido) con notevoli inconvenienti tecnici. Il problema
viene risolto (vedi seguito) portando il fluido al livello
superiore di pressione del ciclo mediante un processo di
compressione nella zona del vapore surriscaldato, e poi,
riducendo la pressione del fluido fino al livello inferiore
di lavoro del ciclo con l'ausilio di una particolare
trasformazione
termodinamica
isoentalpica
detta
CAPITOLO 7B
Elementi di termodinamica
Corso di Fisica Tecnica – a.a. 2010/2011 - Docente: Prof. Carlo Isetti
laminazione o espansione Joule-Thompson (vedi dopo).
In generale, per realizzare questo ciclo frigo si collegano in serie quattro componenti
diversi attraverso i quali il fluido circola subendo cambiamenti di fase da liquido ad aeriforme
e viceversa. In figura è rappresentato uno schema relativo alla dispo-sizione di questi
componenti in un ciclo frigo.
In particolare, i componenti sono:
 un dispositivo per scambiare efficacemente calore (scambiatore di calore) attraverso il
quale il fluido a temperatura e pressione più bassa riceve il calore Q2 dall'esterno;
 un propulsore (compressore) che comprima il fluido (vapore surriscaldato) fino al livello
superiore di pressione del ciclo mediante uno scambio di lavoro L;
 un secondo scambiatore di calore lungo il quale il fluido si prima si raffreddi e poi passi
allo stato liquido cedendo una quantità di calore Q1 = - Q2 + L all'esterno;
 un organo di espansione o valvola di laminazione attraversando la quale il fluido passa dal
livello superiore di pressione a quello inferiore.
E' opportuno aprire una breve parentesi per illustrare il funzionamento dell'organo o
valvola di espansione. In figura è schematizzato tale dispositivo attraverso il quale transita il
fluido frigorigeno; l'elemento tratteggiato rappresenta un setto in materiale poroso che
introduce lungo il percorso del fluido una notevole perdite di carico.
Si consideri il sistema aperto individuato dalle sezioni 1 e 2. Il processo di efflusso del fluido
tra queste sezioni può essere considerato, con ottima approssimazione adiabatico.
CAPITOLO 7B
Elementi di termodinamica
Corso di Fisica Tecnica – a.a. 2010/2011 - Docente: Prof. Carlo Isetti
In condizioni di regime stazionario l'equazione di bilancio dei sistemi aperti fornisce:
Q12 - L' = h2 - h1 + Ec + Ep
Dimensionando opportunamente il setto poroso e cioè regolando le perdite di carico
attraverso questo si realizza la condizione Ec  0. Poichè è inoltre trascurabile l'effetto delle
differenze di quota tra i baricentri delle sezioni è anche Ep  0 ed essendo, inoltre, per
ipotesi, evidentemente nulli anche i termini Q12 e L', si ottiene dall'equazione di bilancio:
h2 = h1
ossia, la trasformazione è isoentalpica.
Nella seguente figura le trasformazioni di questo semplice ciclo frigorigeno sono
rappresentate sul diagramma (P, h), molto utilizzato nella tecnica frigorifera.
Si esaminino ora singolarmente le varie trasformazioni.

Tratto A  B: il fluido (alla pressione e temperatura inferiore del ciclo) passa dallo stato
termodinamico A (quasi tutto il fluido è allo stato liquido) a quello di vapore saturo secco
B. Essendo il processo di evaporazione isobaro (e anche isotermo), il calore Q2 > 0
scambiato con l'esterno e cioè assorbito dal fluido è per unità di massa di fluido:
Q2 = hB - hA (kJ/kg)
La differenza hB - hA può leggersi direttamente sulle ascisse del diagramma (P, h). Lo
scambiatore di calore ove si verifica questo processo di evaporazione viene detto
evaporatore.

Tratto B  C: il fluido viene aspirato e compresso dal compressore subendo una
trasformazione adiabatica.. All'uscita dal compressore la pressione del fluido è pari alla
pressione di lavoro superiore del ciclo. Si noti che lo stato C è uno stato di vapore
surriscaldato per cui la temperatura TC è superiore a alla temperatura di condensazione del
fluido Tc’. Applicando l'equazione di bilancio dei sistemi aperti tra l'aspirazione e la
mandata del compressore si ottiene, (processo adiabatico con Ec = Ep = 0) si ottiene:
L' = - (hC - hB ) [kJ/kg]
La differenza hC - hB può leggersi direttamente sulle ascisse del diagramma (P, h).
CAPITOLO 7B
Elementi di termodinamica
Corso di Fisica Tecnica – a.a. 2010/2011 - Docente: Prof. Carlo Isetti

Tratto C  C'  D: il fluido, a partire dalla temperatura TC e a Pc = cost. si raffredda
dapprima cedendo calore all'esterno fino a raggiungere la temperatura di condensazione
(stato di vapore saturo secco C') e condensa a Pc e Tc’ costanti fino allo stato D (stato di
liquido saturo) poi continuando a cedere calore. Essendo l'intero processo C  C' D
isobaro, il calore Q1 ceduto dal fluido è:
Q1 = hD - hC [kJ/kg]
e, pertanto, può ancora leggersi direttamente sulle ascisse del diagramma (P, h).

Tratto D  A: il fluido si espande isoentalpicamente attraverso una valvola di
laminazione (di solito costituita da un lungo condotto capillare) riducendo la propria
pressione fino a quella vigente all'evaporatore. Il fluido che in D è tutto allo stato liquido
si ritrova in A parzialmente vaporizzato. L'effetto utile di questo ciclo è:
COPf = -Q2 / L = (IB - IA) / (IC - IB)
Se si moltiplica il numeratore e il denominatore dell'espressione COPf per la portata massica
qm di fluido frigorigeno che circola nell'impianto, si ha anche:
COPf = qm (hB - hA) / qm (hC - hB) = f / P
Il prodotto:
f = qm (hB - hA)
rapprenta la potenza frigorigena (potenza termica asportata) e il prodotto qm (hC - hB) la
potenza meccanica spesa P.
CAPITOLO 7B
Elementi di termodinamica