Conosciamo tutti la necessità di usare i numeri col segno, i numeri relativi.
+ 4000 potrebbe essere l’altitudine di una montagna, - 4000 invece potrebbe essere la profondità di un
mare.
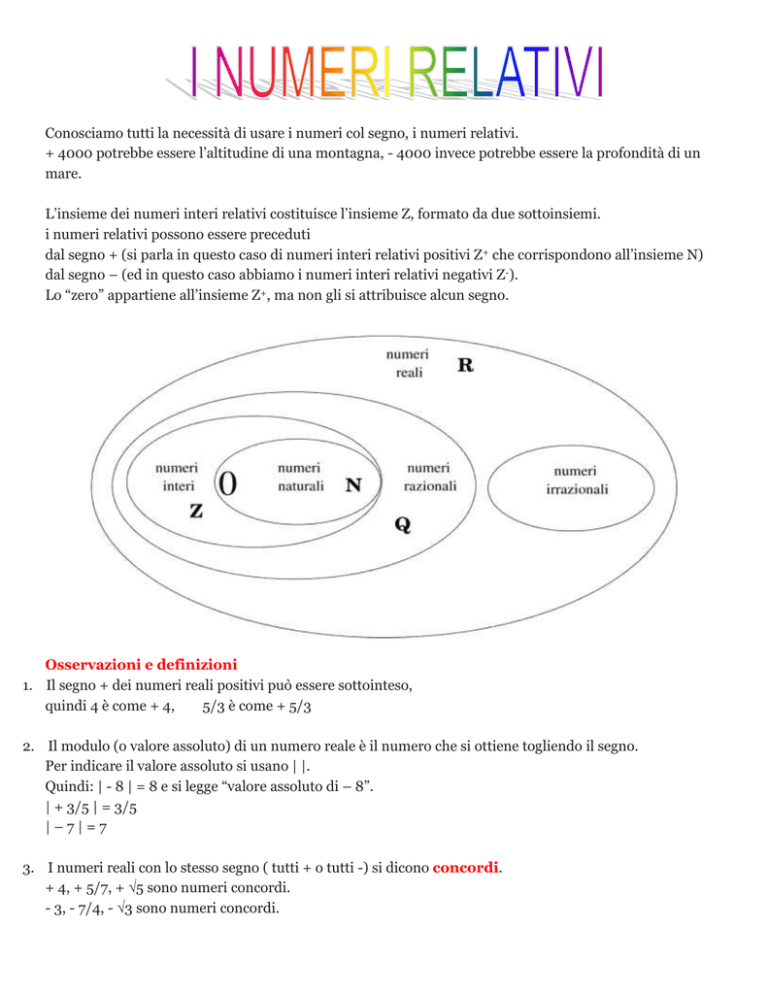
L’insieme dei numeri interi relativi costituisce l’insieme Z, formato da due sottoinsiemi.
i numeri relativi possono essere preceduti
dal segno + (si parla in questo caso di numeri interi relativi positivi Z+ che corrispondono all’insieme N)
dal segno – (ed in questo caso abbiamo i numeri interi relativi negativi Z-).
Lo “zero” appartiene all’insieme Z+, ma non gli si attribuisce alcun segno.
Osservazioni e definizioni
1. Il segno + dei numeri reali positivi può essere sottointeso,
quindi 4 è come + 4,
5/3 è come + 5/3
2. Il modulo (o valore assoluto) di un numero reale è il numero che si ottiene togliendo il segno.
Per indicare il valore assoluto si usano | |.
Quindi: | - 8 | = 8 e si legge “valore assoluto di – 8”.
| + 3/5 | = 3/5
|–7|=7
3. I numeri reali con lo stesso segno ( tutti + o tutti -) si dicono concordi.
+ 4, + 5/7, + 5 sono numeri concordi.
- 3, - 7/4, - 3 sono numeri concordi.
I numeri reali con diverso segno si dicono discordi. + 4 e – 5/2 sono numeri discordi.
4. Due numeri discordi con lo stesso valore assoluto si dicono opposti.
-5 e + 5 sono numeri opposti.
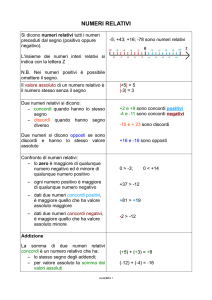
CONFRONTO DI NUMERI RELATIVI
Confrontando dei numeri concordi positivi è maggiore quello che ha maggior valore assoluto.
+ 7,6 è maggiore di + 4,5
+ 7,6 > + 4,5
Confrontando dei numeri concordi negativi è maggiore quello che ha minor valore assoluto.
- 6 è maggiore di – 8
-6>-8
Confrontando due numeri discordi è sempre maggiore il numero reale positivo.
+ 8 è maggiore di – 23
+ 8 > - 23
ADDIZIONE di numeri CONCORDI
ADDIZIONE di numeri DISCORDI
SOTTRAZIONE di numeri RELATIVI
Per trovare la differenza di due numeri relativi possiamo addizionare al primo l’opposto
del secondo.
Poiché con i numeri relativi la sottrazione, in pratica, diventa un’addizione, ecco che possiamo ricondurre
una successione di addizioni e sottrazioni fra numeri relativi ad un’unica operazione, chiamata addizione
algebrica che ci darà un risultato detto somma algebrica.
Esercizi
Svolgimento:
Compito:
Pag. 26 n. 32, 35
Le moltiplicazioni e le divisioni con i numeri relativi
Il prodotto di due numeri relativi è un terzo numero che ha come valore assoluto il prodotto dei valori
assoluti e come segno vale la seguente regola:
Esempi:
La divisione di due numeri relativi è un terzo numero che ha come valore assoluto la divisione dei valori
assoluti e come segno vale la stessa regola del prodotto.
Esempi:
Esercizi:
Compito:
Pag. 35 n. 158, 160
Pag. 36 n. 183, 185
La potenza di numeri relativi
La potenza di un numero relativo è il prodotto di tanti fattori, ciascuno uguale alla base, quante sono le
unita dell’esponente.
(−𝟑)𝟓 = (−𝟑) ∙ (−𝟑) ∙ (−𝟑) ∙ (−𝟑) ∙ (−𝟑) = +𝟖𝟏
Se la base è positiva, il risultato della potenza è sempre un numero relativo positivo.
Se la base è negativa
se l’esponente è pari, il risultato della potenza è un numero relativo positivo.
se l’esponente è dispari, il risultato della potenza è un numero relativo negativo.
Proprietà delle potenze
Valgono le stesse proprietà delle potenze dei numeri naturali. Studiarle a pagina 15 del libro di Algebra E.
0
In particolare (−7)
=1
Potenza con esponente negativo
Valgono le stesse regole dei numeri razionali.
Esempio:
(−3)−3 =
(+5)−2 =
1
(−3)3
=
1
−27
= −
1
27
1
1
1
=
=
+
(+5)2 +25
25
Compito:
Pag. 37 n. 193, 197, 204, 209
Radici quadrate e radici cubiche
Affinchè si possa calcolare una radice quadrata, è necessario che il radicando sia positivo. Non è possibile
calcolare la radice quadrata di un numero negativo.
√16 = 4 𝑝𝑒𝑟𝑐ℎè
42 = 16
√−36 𝑖𝑚𝑝𝑜𝑠𝑠𝑖𝑏𝑖𝑙𝑒 𝑝𝑒𝑟𝑐ℎè 𝑛𝑜𝑛 𝑒𝑠𝑖𝑠𝑡𝑒 𝑛𝑒𝑠𝑠𝑢𝑛 𝑛𝑢𝑚𝑒𝑟𝑜 𝑐ℎ𝑒 𝑎𝑙 𝑞𝑢𝑎𝑑𝑟𝑎𝑡𝑜 𝑓𝑎𝑐𝑐𝑖𝑎 − 36
Si può sempre calcolare la radice cubica di un numero, indipendentemente dal suo segno.
3
√+8 = +2 𝑝𝑒𝑟𝑐ℎè
3
√−27 = −3 𝑝𝑒𝑟𝑐ℎè
(+2)3 = +8
(−3)3 = −27
Le stesse regole delle 4 operazioni e delle potenze dei numeri relativi possono essere applicate ai numeri
razionali.
Compito:
Pag. 39 n. 242, 248, 255
Pag. 40 n. 264, 293, 299, 318
Pag. 44 n.336
Pag. 47 esercizi di autovalutazione con soluzioni
Pag. 50 n. 2, 7, 8
FITNESS Pag. 55, 56, 57