Teoria Neoclassica della Crescita

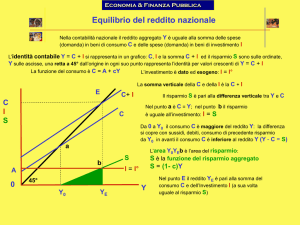
La teoria neoclassica della crescita economica
La teoria neoclassica della crescita sostiene che la crescita
economica è causata da:
• aumento della quantità di lavoro L utilizzata (crescita della
popolazione)
• aumento della qualità del lavoro L grazie a istruzione e
formazione
• aumento dello stock di capitale K (attraverso più risparmio S
e investimento I)
• miglioramenti della tecnologia produttiva.
Lo sottosviluppo è visto come il risultato dell’inefficiente
utilizzo delle risorse e dell’intervento dello Stato nei mercati
attraverso il controllo regolato dei prezzi.
1
La teoria neoclassica della crescita economica
• Gli economisti neoclassici sostengono che l’intervento dello
Stato nell’economia, attraverso controllo e amministrazione,
freni la crescita perché incoraggia la corruzione e l’inefficienza
e non permette alla motivazione imprenditoriale di esprimersi.
• Di conseguenza, le cause alla radice dello sottosviluppo si
nascondono nei Governi degli stessi paesi in via di sviluppo.
•
Solo quando i Governi adottano politiche che mirano a:
de-regolamentare i mercati
limitare l’intervento statale
migliorare il “lato dell’offerta” dell’economia
questa crescerà e si svilupperà ⇒ il livello potenziale di output
tenderà quindi a salire generando crescita economica.
2
Il modello neoclassico di crescita
• L’interpretazione di Solow del modello di Harrod-Domar (HD) si basa sul principio dei rendimenti marginali decrescenti.
• Secondo Solow, il capitale K e il lavoro L contribuiscono a
determinare l’output e, a causa del rendimento marginale
decrescente del capitale, il rapporto capitale-prodotto (K/Y) è
endogeno.
• Il modello di Solow ipotizza che il rapporto capitaleprodotto (K/Y) vari al variare della disponibilità pro-capite di K
dell’economia. La variazione è guidata dalla legge dei
rendimenti marginali decrescenti ⇒ più elevato è il capitale
pro-capite più elevato sarà il rapporto K/Y. Questo contrasta
con il modello H-D, dove l’ipotesi di costanza del rapporto K/Y
elimina la possibilità di rendimenti marginali decrescenti.
3
Il modello neoclassico di crescita
• Mentre in H-D lo stock di capitale (K) dà sempre luogo alla
stessa quantità di prodotto per unità di capitale (Y/K), in
Solow questa diminuisce all’aumentare dello stock (K ha
rendimenti marginali decrescenti).
• La principale implicazione empirica è che il saggio di
risparmio (s) non ha nessun effetto di lungo periodo sulla
crescita. Vi è un livello di stato stazionario (Steady State)
(di lungo periodo) del reddito pro-capite a cui le economie
convergono, indipendentemente dal loro punto di partenza
storico.
• Indipendentemente dal livello iniziale del capitale procapite, due paesi con tassi di risparmio simili, tassi di
deprezzamento del capitale e tassi di crescita della
popolazione convergono a standard di vita di lungo periodo
simili.
4
La funzione di produzione: i rendimenti di scala
La funzione di produzione descrive lo stato della tecnologia
(delle tecniche di produzione) e può essere scritta nel
seguente modo:
Y = F (K , L)
λ Y = F (λK , λ L )
1
Se poniamo λ = L otteniamo che il prodotto per addetto è
funzione del capitale per addetto:
Y
K L
K 
= F( , ) = f
 ⇒ y = f (k )
L
L L
 L 
La proprietà fondamentale della funzione di produzione è,
secondo Solow, quella dei rendimenti di scala costanti
(raddoppiando la scala di produzione, cioè raddoppiando la quantità di
capitale e lavoro, la quantità di prodotto raddoppia. Questa proprietà
consente di esprimere la funzione di produzione in maniera intensiva)
5
La funzione di produzione: i rendimenti
decrescenti
Secondo i neoclassici la funzione di produzione intensiva
(prodotto per addetto) presenta rendimenti marginali
decrescenti dei fattori produttivi capitale K e lavoro L.
YY/L
K/L
Studiamo ora l’evoluzione nel tempo dell’accumulazione di
capitale ….
6
Il modello di Solow senza progresso tecnico
α 1−α
(1) Y = K L
Funzione di produzione di tipo Cobb-Douglas
α
y
=
k
(2)
Funzione di produzione in termini pro capite
derivata dalla (1) dividendo per
L dove y = Y / L e k = K / L
(3) ∆ K = sY − dK Equazione degli investimenti (è incorporata la
condizione di equilibrio S=I)
Se ragioniamo in termini pro capite otteniamo che:
(6) ∆ k = sy − dk
Questa è l’equazione dinamica del sistema del modello di Solow
(in assenza di progresso tecnico). Quando gli investimenti sono
appena sufficienti a coprire il deprezzamento del capitale, allora la
variazione del capitale è nulla (cioè lo stock di capitale
dell’economia non aumenta).
7
La soluzione di stato stazionario
Riscriviamo l’equazione (4) sostituendo il valore della funzione
di produzione e ponendo la variazione del k uguale a zero,
otteniamo il valore del capitale per addetto di stato stazionario
∆ k = 0 ⇒ sf ( k ) − dk = 0 ⇒ sf ( k ) = dk
α
y
=
f
(
k
)
=
k
Nel nostro caso
quindi
sk
α
= dk ⇒ sk
α −1
 s 
= d ⇒ k* = 

 d 
1
1−α
Sostituendo il valore dello stock di capitale per addetto nella
funzione di produzione, si ottiene il PIL/per addetto di stato
 s 
stazionario y * =  d 
α
1−α
.
8
La soluzione di stato stazionario
• L’equazione finale mette in evidenza che a livelli più elevati
del tasso di risparmio (ossia a valori più elevati del tasso di
investimento) corrispondono livelli più elevati del prodotto per
addetto ⇒ livelli più elevati del PIL pro-capite.
• Esiste, dunque, nel modello di Solow, in assenza progresso
tecnico, una relazione positiva fra il livello degli investimenti e
il livello del PIL pro-capite, ossia fra il livello degli investimenti
e il livello di benessere materiale e di sviluppo, che può essere
studiata empiricamente.
9
Tasso di risparmio e crescita del prodotto
• Dato che l’accumulazione di capitale in stato stazionario è
nulla allora anche il tasso di crescita del prodotto per addetto
y sarà nullo. Pertanto, indipendente dal tasso di risparmio,
nello stato stazionario l’accumulazione di K si arresta.
• Il tasso di risparmio aumenta il livello di benessere di lungo
periodo, ma non influisce sui tassi di crescita. Tuttavia, se
un’economia (per assurdo) risparmiasse tutto il prodotto per
addetto, il consumo sarebbe nullo! D’altro canto, se il
risparmio è nullo, non vi è alcun processo di accumulazione.
• Qual è quindi il livello ottimo di risparmio? (quel livello di
risparmio chiamato della regola aurea che dà luogo ad un
tasso di crescita ottimale).
10
Il modello di Solow con progresso tecnico e
crescita della popolazione
Il progresso tecnico assume diverse forme, ipotizziamo che il
progresso tecnico aumenti l’efficienza del lavoro. L’efficienza
del lavoro riflette le conoscenze della società, circa i metodi di
produzione.
Se ipotizziamo che Y = F(K, A*L) dove A*L è la quantità di
lavoro in unità di efficienza. Se, ad esempio, A raddoppia ogni
anno è che come se l’economia avesse ogni anno un numero
doppio di lavoratori. In questo caso, si dice che il progresso
tecnologico è accrescitivo di lavoro.
11
Il modello di Solow con progresso tecnico e
crescita della popolazione
Anche se la forza lavoro L raddoppia, la quantità di lavoro
raddoppia. Complessivamente, se l’efficienza del lavoro A
(progresso tecnico) aumenta ad un tasso gA e se la forza
lavoro L aumenta ad un tasso gL, la quantità di lavoro per
unità di efficienza aumenta ad un tasso pari a gA + gL.
Ipotizziamo sempre rendimenti di scala costanti, ossia se
raddoppiamo la quantità di capitale e di lavoro in unità di
efficienza anche la produzione complessiva raddoppierà.
Questa proprietà consente di esprimere la funzione di
Y
K 
= F ,1 = f (k )
produzione in unità di efficienza AL
 AL 
12
Il modello di Solow con progresso tecnico e
crescita della popolazione
Ipotizziamo sempre rendimenti marginali decrescenti del
capitale per unità di lavoro efficiente. Risolvendo come nel
caso senza progresso tecnologico otteniamo che:
∆ K = sY − dK
Se riscriviamo l’equazione in termini pro capite abbiamo che:
∆K
K
= s
Y
K
− d
K
K
.
Il tasso di accumulazione è costante se e solo se il rapporto
Y/K è costante, ossia se Y e K crescono allo stesso tasso.
Consideriamo ora il tasso di crescita del capitale per unità di
lavoro efficiente K/AL.
13
Se ipotizziamo che il tasso di crescita della forza lavoro sia pari
ad gL e che il tasso di crescita del progresso tecnico sia pari
gA esogeno, facendo le opportune sostituzioni avremo che:
∆k = sy − (d + g L + g A )k
L’accumulazione di capitale cessa quando il livello degli
investimenti I riesce a mantenere costante il livello del capitale
per unità di lavoro efficiente, ossia quando riesce a coprire
l’aumento del lavoro per unità di efficienza (che aumenta al
tasso gA + gL) e il tasso di deprezzamento pari a d.
14
La soluzione di stato stazionario
Il livello del prodotto per unità di lavoro efficiente, in stato
stazionario, dipende positivamente dal livello della tecnologia
e dal tasso di risparmio e negativamente dal tasso di crescita
della popolazione
In questo caso qual è il tasso di investimento che mantiene
inalterato il capitale per unità di efficienza? Mentre in assenza
di progresso tecnico per mantenere costante il capitale era
sufficiente investire un ammontare pari al deprezzamento del
capitale, in questo caso bisogna tener conto che il lavoro per
unità di efficienza aumenta al tasso gA + gL.
Complessivamente, quindi, è necessario investire un
ammontare pari a K*( gA + gL +d). L’investimento per unità di
lavoro efficiente è pari a (K/AL)*( gA + gL +d).
15
Il modello di Solow con progresso tecnico e
crescita della popolazione
• La dinamica dell’accumulazione di capitale è simile al caso
di assenza di progresso tecnico.
• Nel punto iniziale, l’investimento I eccede la quantità di
capitale K ed è più che sufficiente a mantenere inalterato il
capitale per unità di efficienza, per cui il capitale in unità di
efficienza aumenta.
• Il processo si arresta quando l’investimento per unità di
lavoro efficiente è pari all’espressione di cui sopra.
16
Crescita bilanciata e tasso di risparmio
• In stato stazionario, il prodotto per unità di lavoro efficienti
è costante. Quindi, poiché la quantità di lavoro in unità di
efficienza aumenta ad un tasso pari a gA + gL, è necessario
che il prodotto aumenti ad un tasso uguale pari a gA + gL.
Anche in questo caso, quindi, il tasso di crescita di lungo
periodo del prodotto non dipende dal tasso di risparmio.
• Poiché il tasso si crescita del prodotto Y è pari a gA + gL e
quello di L è pari a n, il tasso di crescita di Y/L è pari a gA +
gL − gL = gA
• Lo stato in cui capitale, lavoro in unità di efficienza e
prodotto aumentano al tasso gA + gL viene chiamato
sentiero di crescita bilanciata.
17
Crescita bilanciata e tasso di risparmio
Le conclusioni relative agli effetti di un aumento del tasso di
risparmio rimangono invariate:
• un aumento del saggio di risparmio s aumenta il tasso di
crescita del prodotto in unità di efficienza per un periodo di
tempo, ma nel lungo periodo non ha alcun effetto.
• Il tasso di risparmio s determina il livello del prodotto per
unità di lavoro efficiente ma non influisce sul suo tasso di
crescita di lungo periodo: la variazione del tasso di risparmio
ha, nel lungo periodo, un effetto sul livello del reddito, ma
non sul suo tasso di crescita.
18