La Fattorizzazione degli interi con i numeri di Fibonacci
Di Cristiano Armellini ([email protected])
La successione di Fibonacci (forse una delle successioni numeriche più famose) è quella per cui a partire dai
valori 0, 1 si ottiene il successivo termine sommando i due precedenti:
F(0) = 0, F(1) = 1, F(n) = F(n-1)+F(n-2) per n = 2, 3, 4, 5…..
Ovvero F(n+2)-F(n+1)-F(n)=0
E’ facilmente dimostrabile che l’ennesimo numero della serie di Fibonacci è rappresentato dalla formula:
1
1 √5
1 √5
2
2
√5
Ci sono molte proprietà che legano i numeri di Fibonacci con i numeri primi:
1) La successione di Fibonacci contiene infiniti numeri primi (congettura non dimostrata)
2) Ogni primo è un fattore di qualche numero di Fibonacci
In particolare la proprietà 2) ci suggerisce un metodo per impiegare i numeri di Fibonacci nella
fattorizzazione dei numeri interi.
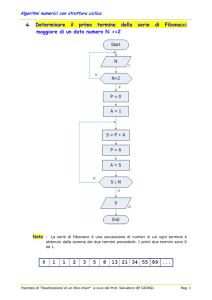
ALGORITMO :
Supponiamo che n = pq con p, q primi. L’idea è di calcolare per ogni numero di Fibonacci j il MCD(n, j): se il
MCD(n, j) non è l’unità allora deve essere necessariamente uno tra i fattori p, q del numero n.
Usando il PARI/GP possiamo scrivere il codice:
{fact(p) =
n = 2;
k = fibonacci(n);
while (gcd(p, k) == 1, n = n+1 ;k =fibonacci(n) );
g = gcd(p, k);
print(g);}
Dove il GCD (massimo comun divisore) e “Fibonacci” sono funzioni predefinite gia presenti nel programma
PARI/GP
Volendo possiamo scrivere il codice anche per il Massimo comun divisore e per i numeri di Fibonacci.
In C una possibile versione è:
long Fibonacci (long n){
if (n ==0) return 0;
else
if (n ==1) return 1;
else return Fibonacci(n-1)+ Fibonacci(n-2);
}
long MCD(long a, long b) {
if (a==b) return a;
else
if (a > b) return MCD(a-b, b);
else (a< b) return MCD(b, a);
}
Naturalmente esistono anche altre implementazioni.
Per numeri grandi da fattorizzare possiamo sempre partire nella successione di Fibonacci non da n = 2 ma
da n = k dove k è un numero abbastanza elevato.