Fisica
Facoltà di Ingegneria, Architettura e delle
Scienze Motorie
Lezione 6 maggio 2013
Architettura
(corso magistrale a ciclo unico quinquennale)
Prof. Lanzalone Gaetano
Macchine Termiche
Le macchine termiche
• Il primo principio permette di trasformare
energia interna e calore in lavoro meccanico
•
•
•
Le macchine che realizzano queste trasformazioni di chiamano
“macchine termiche”
esempi di macchine termiche:
– Il motore dell’automobile
– Le vecchie locomotive a vapore
Gli stessi principi vengono utilizzati dai
– Frigoriferi, condizionatori, pompe di calore
P
Pi
i
f
Pf
Τ
Vi
ΔU = 0
•
•
•
•
•
•
Vf
Q=L
Una espansione isoterma trasforma tutto il calore assorbito dal serbatoio di calore a temperatura T in
lavoro meccanico
Una volta raggiunta la pressione atmosferica l’espansione si arresta
Così anche la produzione di lavoro
Occorre riportare il sistema al punto di partenza e ripetere l’espansione
La macchina termica deve operare su un ciclo
Perché ci sia una reale produzione di lavoro occorre far tornare indietro il sistema lungo una isoterma a
temperatura più bassa
V
Rendimento di una macchina termica
•
Se si torna indietro lungo una isoterma a temperatura più bassa,
– il lavoro da effettuare, area in rosa, per riportare il
sistema nello stato iniziale è più piccolo di quello ottenuto
nella prima fase
– Nel ciclo si ottiene una produzione netta, positiva, di lavoro
del sistema sull’ambiente esterno
• Il lavoro è rappresentato dall’area racchiusa dal ciclo
• Se il ciclo viene percorso in verso orario, come è il caso
descritto, il lavoro è positivo (il sistema fa lavoro
sull’esterno)
P
Pi
ΔU = Q − L
i ΔU i →i = 0 ⇒ L = Q
h
f
Pf
Τ
g
Vi
Vf
• Se il ciclo viene percorso in verso antiorario, il lavoro è negativo, allora è l’ambiente esterno ad
effettuare un lavoro sul sistema •
Si osservi che sulla isoterma if il sistema assorbe un calore Q pari al lavoro effettuato (area sotto la
trasformazione, in colore grigio)
•
Nella isoterma gh il calore è negativo, viene ceduto dal sistema all’ambiente esterno
•
Lungo le isocore in una il calore viene assorbito (hi) nell’altra viene ceduto (gf).
•
Si definisce rendimento di una macchina termica il rapporto tra il lavoro prodotto nel ciclo e il calore
comunque assorbito nel ciclo:
V
Macchine termiche che lavorano tra due serbatoi
Le macchine termiche sono sistemi termodinamici che descrivono un ciclo
• C’è una parte del ciclo in cui il sistema assorbe calore da uno o più serbatoi
presenti nell’ambiente esterno
• C’è un’altra parte del ciclo in cui il sistema cede calore ad uno o più
serbatoi presenti nell’ambiente esterno
ΔU = Q − L
ΔU = 0 ⇒ L = Q
Nel ciclo il sistema esegue un lavoro netto positivo sull’ambiente esterno •
•
Un caso particolare di macchina termica è quella che lavora tra due
serbatoi
– Schematizzabile come nella figura a lato
– La macchina assorbe calore Q1 dal serbatoio a temperatura più
elevata T1 – Cede il calore Q2 al serbatoio a temperatura inferiore T2 – Produce il lavoro L
Il rendimento della macchina è dato da
•
In questo caso:
L
La macchina e il ciclo di Carnot
La macchina di Carnot è una macchina reversibile che opera con due soli serbatoi di calore
Il ciclo è costituito da • due isoterme (alle temperature T1 e T2) (ab e cd)
• e da due adiabatiche (è l’unica trasformazione reversibile che non
richiede ulteriori serbatoi di calore) (bc e da)
Nella figura è rappresentato il ciclo di Carnot percorso da un gas perfetto
L
•
Scegliendo il punto b dove far finire
l’espansione isoterma, si può variare il
lavoro fatto dalla macchina in un ciclo.
•
•
Tutte le macchine reversibili che operano con due soli serbatoi di
calore sono macchine di Carnot
Il ciclo può essere percorso da una qualsiasi sostanza: gas
perfetto, gas reale, acqua e vapor d’acqua, freon, etc. Conseguenze del teorema di Carnot
•
•
•
Dati due termostati a temperatura diversa, la maniera più efficiente per
trasformare calore in lavoro meccanico è quello di utilizzare una macchina di
Carnot. il rendimento di una macchina di Carnot è indipendente dalla sostanza impiegata
per percorre il ciclo, gas perfetto, gas reale, acqua e vapore d’acqua, freon. etc,
dipende solo dalle temperature dei termostati tra cui opera: – Abbiamo già calcolato il rendimento di una macchina di Carnot operante con
un gas perfetto
Tutte le macchine di Carnot operanti tra questi due termostati avranno tutti lo
stesso rendimento appena calcolato.
Il frigorifero
•
•
•
Il ciclo di Carnot è un ciclo reversibile
Quindi può essere percorso all’indietro
Ma quando una trasformazione viene percorsa al contrario – Si invertono i segni degli scambi energetici
– Sicuramente cambia segno ΔU tra due stati – Ma anche quelli di L e Q che si invertono
– Quelle che erano le quantità assorbite diventano cedute
e viceversa
•
quindi la macchina di Carnot al contrario – cede la quantità di calore Q1 al serbatoio più caldo
– assorbe il lavoro L
– assorbe il calore Q2 dal serbatoio più freddo
•
Abbiamo realizzato un frigorifero
Si definisce coefficiente di prestazione del frigorifero
L
Q2
Q2
ε=
=
L Q1 − Q2
Il secondo principio della Termodinamica
Enunciato di Kelvin-Plank (Primo Enunciato)
•
•
•
•
Le macchine termiche sono sistemi termodinamici che
descrivono un ciclo
C’è una parte del ciclo in cui il sistema assorbe calore da
uno o più serbatoi presenti nell’ambiente esterno
C’è un’altra parte del ciclo in cui il sistema cede calore ad
uno o più serbatoi presenti nell’ambiente esterno
Nel ciclo il sistema esegue un lavoro netto positivo
sull’ambiente esterno
L(=Q1)
E’ impossibile realizzare un processo il cui unico
risultato sia quello di assorbire calore da un serbatoio e
di convertirlo completamente in lavoro.
Il secondo principio della Termodinamica
Enunciato di Clausius (Secondo Enunciato)
“Non è possibile realizzare una trasformazione il
cui unico risultato sia quello di far passare del
calore da un corpo a temperatura minore ad uno
a temperatura maggiore.” Oppure “È
impossibile
che
il
calore
passi
spontaneamente da un corpo più freddo ad uno
più caldo”
• Il passaggio di calore da un corpo più freddo
ad uno più caldo deve essere sempre
accompagnato da qualche altra modifica da
qualche altra parte nell’universo
à Ossia c’è bisogno di un lavoro esterno
Verifica dell’equivalenza tra le due formulazioni
Si può vedere che violando una formulazione è violata anche l’altra. VERIFICHIAMO. Supponiamo, per assurdo (negando il primo enunciato) che esista una
macchina termica che riesca a trasformare tutto il calore estratto da un serbatoio a
temperatura T1 in lavoro meccanico. • Allora, è possibile usare questa macchina (1) accoppiandola ad una macchina di Carnot (2) che
lavorara come frigorifero
– Il lavoro prodotto dalla prima macchina viene utilizzato per far funzionare il frigorifero
Macchina Termica (1)
Macchina Frigorifera (2)
Τ1
Q1
Τ1
L
W
L Q'1
W
Q1
L= Q1
L=Q1
Q2
Q2
Τ2
•
Τ2
Macchina Frigorifera (3)
Macchina Ter+Frig (1+2)
Τ1
Τ1
Q'1= Q2+ Q1
≡
Τ2
Q2
Q2
Τ2
L’effetto cumulativo delle due macchine (1+2) è un frigorifero ideale (3) che preleva il
calore Q2 dal serbatoio più freddo e lo trasferisce a quello più caldo senza richiedere alcun
lavoro dall’esterno. Questa macchina
viola la seconda formulazione del II principio
Irreversibilità e II° principio
•
Il secondo principio della termodinamica fa capire perché alcune trasformazioni
sono irreversibili
•
Prendiamo il passaggio di calore tra due corpi inizialmente a temperatura
differente:
– Il secondo principio ci impedisce di realizzare la condizione di partenza perché
bisogna trasferire del calore da un corpo più freddo ad uno più caldo è per fare
questo occorre produrre qualche altra modifica da qualche altra parte
nell’universo
•
Prendiamo un pendolo messo in oscillazione che dopo un po’ si ferma perdendo la
sua energia meccanica in energia interna dell’aria e dei corpi interessati
– Per ripristinare la situazione iniziale occorrerebbe estrarre dall’aria e dai corpi
questa energia interna e ritrasformala, tutta, in lavoro (energia meccanica)
– Il secondo principio ci impedisce di fare questo: una parte dell’energia non può
essere trasformata in lavoro meccanico e deve essere ceduta ad un serbatoio a
temperatura più bassa.
L’entropia
Esiste una funzione di stato che chiameremo entropia, S, tale che l’integrale del
calore infinitesimo scambiato reversibilmente diviso per la temperatura a cui
avviene lo scambio, effettuato su una trasformazione reversibile che connette lo
stato iniziale i e lo stato finale f, è dato dalla differenza dei valori della funzione S
nello stato finale meno quello dello stato iniziale
f
∫
i
R
•
•
δQ R
= Sf − Si
T
Sf − Si = ΔS
Essendo S una funzione di stato, quando un sistema passa dallo stato iniziale i allo stato
finale f, la variazione di entropia è sempre la stessa qualunque sia la trasformazione
utilizzata (reversibile o irreversibile).
il calcolo della variazione di entropia si può fare solo su una trasformazione reversibile.
– Se la trasformazione che stiamo studiando è reversibile allora non c’è problema, basta
applicare la definizione alla trasformazione.
– Se invece la trasformazione è irreversibile, occorre innanzitutto sostituire la
trasformazione data con una reversibile (o più trasformazioni) che fa passare il sistema
dallo stesso stato iniziale allo stesso stato finale, e poi applicare la definizione.
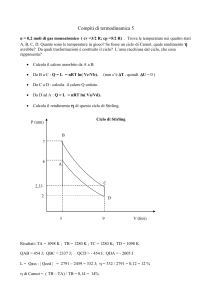
Problema
•
In un cilindro, munito di un pistone a tenuta, sono contenute 10 mol di idrogeno
alla pressione atmosferica . Il gas viene riscaldato a pressione costante dalla
temperatura di 30 °C alla temperatura di 40°C, tenendolo a contatto con un
serbatoio di calore alla temperatura di 50°C.
Supponendo che durante la trasformazione il gas si comporti come un gas
perfetto, determinare:
– Il lavoro fatto dal gas.
– La variazione di energia interna.
Pe=1atm
Θ
50°C
•
•
La trasformazione è irreversibile (assenza di equilibrio termico: temperatura del gas diversa dalla temperatura del
serbatoio (ambiente))
Bisogna usare i parametri dell’ambiente per determinare il lavoro:
L = Pe (V f − Vi )
•
•
Vanno determinati i volumi iniziale e finale
nRTi
Pi Vi = nRTi ⇒ Vi =
Pi
J
10mol × 8.31
303.15K
nRTi
3
molK
Vi =
=
=
0.249m
Pi
1.01× 10 5 Pa
Il volume iniziale
Pe=1atm
Θ
50°C
•
nRTf
Pf Vf = nRTf ⇒ V f =
Pf
J
nRT f 10 mol × 8.31 molK 313.15 K
Vf =
=
= 0.258m3
5
Pf
1.01 ×10 Pa
Il volume finale
L = Pe (V f − Vi ) = 1.01×105 Pa × (.258 − .249)m3 = 909J
•
In un cilindro, munito di un pistone a tenuta, sono contenuti 20 grammi di idrogeno (molecola H2, massa molecolare M=2 u)
alla pressione atmosferica (1.01x105 Pa). Il gas viene riscaldato a pressione costante dalla temperatura di 30 °C alla
temperatura di 40°C, tenendolo a contatto con un serbatoio di calore alla temperatura di 50°C.
Supponendo che durante la trasformazione il gas si comporti come un gas perfetto, determinare:
–
–
Il numero di moli.
Il lavoro fatto dal gas.
– La variazione di energia interna.
•
La variazione di energia interna
•
Il gas è biatomico
ΔU = nC VΔT
CV =
5
R
2
5
J
ΔU = nC VΔT = 10mol × × 8.31
10K = 2077.5J
2
molK
ΔU = 2077.5 J
Pe=1atm
•
La variazione di energia interna
•
Il gas è biatomico
ΔU = nC VΔT = 10mol ×
ΔU = nC VΔT
CV =
5
R
2
5
J
× 8.31
10K = 2077.5J
2
molK
Θ
50°C