+ax2+bx+c>0 +ax2+bx+c<0

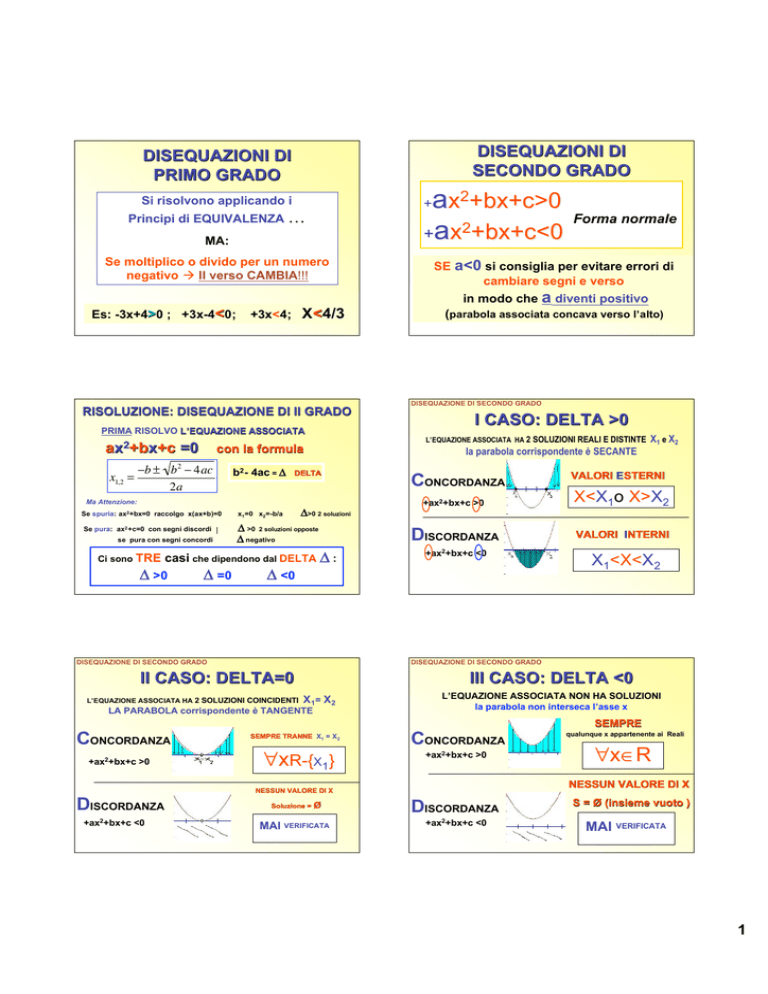
DISEQUAZIONI DI
SECONDO GRADO
DISEQUAZIONI DI
PRIMO GRADO
Si risolvono applicando i
Principi di EQUIVALENZA …
MA:
Se moltiplico o divido per un numero
negativo  Il verso CAMBIA!!!
CAMBIA!!!
Es: -3x+4>0 ; +3x-4
3x-4<0;
X<4/3
+3x<4;
RISOLUZIONE: DISEQUAZIONE DI II GRADO
PRIMA RISOLVO L ’EQUAZIONE ASSOCIATA
ax2+bx
+bx+c =0
x1,2 =
con la formula
!b ± b 2 ! 4ac
2a
b2 - 4ac = Δ
DELTA
Ma Attenzione:
Se spuria: ax2+bx=0 raccolgo x(ax+b)=0
Se pura: ax2 +c=0 con segni discordi
se pura con segni concordi
Ci sono TRE
x1=0 x2=-b/a
Δ>0 2 soluzioni
Δ >0 2 soluzioni opposte
Δ negativo
casi che dipendono dal DELTA Δ :
Δ =0
Δ <0
ax2+bx+c>0
+ax2+bx+c<0
+
SE a<0 si consiglia per evitare errori di
cambiare segni e verso
in modo che a diventi positivo
(parabola associata concava verso l’alto)
DISEQUAZIONE DI SECONDO GRADO
I CASO: DELTA >0
L’EQUAZIONE ASSOCIATA HA 2 SOLUZIONI REALI E DISTINTE
la parabola corrispondente è SECANTE
CONCORDANZA
L’EQUAZIONE ASSOCIATA HA 2 SOLUZIONI COINCIDENTI
X<X
X<X1o X>X
X>X2
DISCORDANZA
VALORI INTERNI
+ax2+bx+c <0
DISCORDANZA
+ax2+bx+c <0
X1<X<X
<X<X2
III CASO: DELTA <0
X 1= X 2
LA PARABOLA corrispondente è TANGENTE
+ax2+bx+c >0
VALORI ESTERNI
DISEQUAZIONE DI SECONDO GRADO
II CASO: DELTA=0
CONCORDANZA
X1 e X2
+ax2+bx+c >0
Δ >0
DISEQUAZIONE DI SECONDO GRADO
Forma normale
SEMPRE TRANNE X1 = X2
∀xR-{X1}
L’EQUAZIONE ASSOCIATA NON HA SOLUZIONI
la parabola non interseca l’asse x
CONCORDANZA
+ax2+bx+c >0
SEMPRE
qualunque x appartenente ai Reali
∀x∈R
NESSUN VALORE DI X
NESSUN VALORE DI X
Soluzione = Ø
DISCORDANZA
MAI VERIFICATA
+ax2+bx+c <0
S = Ø (insieme vuoto )
MAI VERIFICATA
1
RIASSUMENDO, ottengo la seguente REGOLA
DISEQUAZIONE DI II GRADO: ax2+bx+c>0;ax2+bx+c<0
Esercizi: VUOI provare ???
1) risolvo equazione associata ax2+bx+c=0
1)
2) applico la
2)
Regola del DELTA
Δ >0
Δ =0
Δ <0
CONCORDANZA
X<X
X<X1o X>X
X>X2
∀x∈ R
∀x∈ R-{X
R-{X1}
X1<X<X
<X<X2
+ax2+bx+c <0
MAI VERIFICATA
MAI VERIFICATA
S=Ø
S=Ø
*NB: per risolvere con ≥ 0 o ≤ 0, se Δ>0 o Δ=0, aggiungo x1 e x2 alla soluzione
7x 2 + 2x ! 0
x2 ! 5 " 0
*
x 2 + 6x + 9 > 0
6)
5x 2 ! x + 1 > 0
8)
+x 2 ! 4x + 3 > 0
Risolvo l’equazione associata
x=
!6x 2 + 14x > 0
* Se c’è “maggiore o uguale” O “minore o uguale” il procedimento non
cambia: dopo aver trovato il risultato si aggiunge l’uguale
Applico regola del DELTA:
c’è +…> concordanza
+2x 2 + 5x ! 3 " 0
2)
Soluzione esercizi 3-4
x 2 ! 4x + 3 = 0
x1 =1;x 2 = 3
4 ± 16 !12 4 ± 2
=
2
2
x=
Applico regola del DELTA:
c’è +…≤ discordanza
+7x 2 + 2x ! 0
x ! (7x + 2) = 0
4)
+x2 ! 5 " 0
Soluzione esercizi 5-6
+x 2 + 6x + 9 > 0
Risolvo l’equazione associata
x=
Applico regola del DELTA
c’è +…> concordanza
6)
+5x ! x +1 > 0
2
!6 ± 36 ! 36 !6 ± 0
=
2
2
!x " R # {3}
x1 = x 2 = !3
5x ! x +1 = 0
+1± 1! 20 +1± !19
x=
=
10
10
!x " R
2
x2 ! 5 = 0
Δ>0
x !" 5#x $ 5
Soluzione esercizi 7-8
8x 2 + 17x + 2 = 0
Applico regola DELTA>0
c’è +…< discordanza
8) !6x 2
+ 14 x < 0
+6x ! 14x > 0
2
Δ<0
Qualunque x appartenente
ai Reali
Δ>0
2
7
Risolvo l’equazione associata
Δ=0
Qualunque x appartenente
ai Reali tranne x=3
Risolvo l’equazione associata
Applico regola del DELTA
c’è +…> concordanza
x 2 + 6x + 9 = 0
2
7
!8x 2 ! 17x ! 2 > 0 Cambio segni e verso
+8x 2 + 17x ! 2 < 0 Risolvo l’equazione associata
7)
5)
0! x!
Applico regola del DELTA
c’è concordanza
!3 " x "1/2
x1 = 0;x 2 = !
x 2 = 5 ! x1,2 = ± 5
x1 = !3" x 2 =1/2
Δ>0
7x 2 + 2x = 0
Risolvo l’equazione associata
Applico regola del DELTA
c’è discordanza
2x 2 + 5x ! 3 = 0
!5 ± 25 + 24 !5 ± 7
=
4
4
3)
Δ>0
x1 <1! x 2 > 3
Risolvo l’equazione associata
esercizi
x 2 !4x + 3>0
!8x 2 ! 17x ! 2 > 0
Soluzione esercizi 1-2
1)
Ricopia e risolvi
le disequazioni proposte
sul tuo quaderno:
Controlla poi i risultati
2x 2 + 5x ! 3 " 0
5)
7)
DISCORDANZA
*
3)
4)
+ax2+bx+c >0
x2 ! 4x + 3 > 0
x=
!17 ± 289 ! 64 !17 ± 15
=
16
2
!16 < x < !1
Δ>0
Cambio segni e verso
Risolvo l’equazione associata
2x(3x ! 7) = 0
7
3
7
x<0!x>+
3
x1 = 0; x2 = +
Applico regola del
DELTA>0
c’è +..> concordanza
x1 = !16; x2 = !1
+6x 2 ! 14 = 0
Δ>0
2