Servizio Nazionale di Valutazione

 Servizio Nazionale di Valutazione
a.s. 2014/15
Guida alla lettura
Prova di Matematica
Classe seconda – Scuola secondaria di II grado
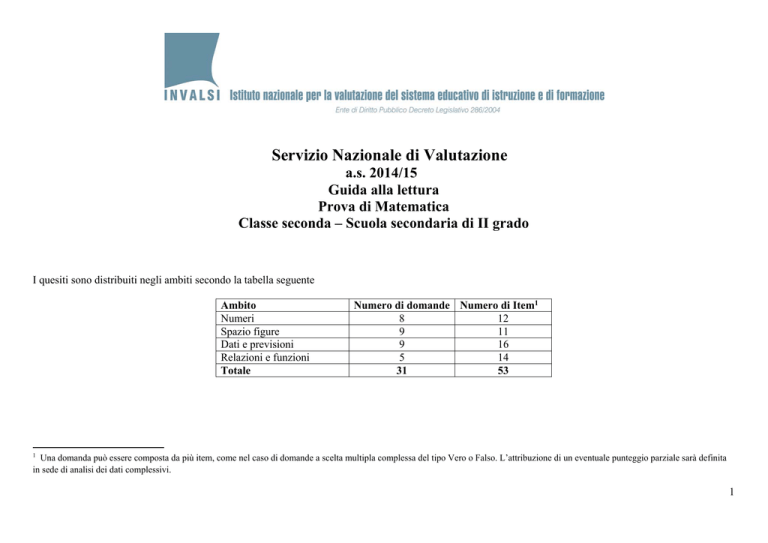
I quesiti sono distribuiti negli ambiti secondo la tabella seguente
Ambito
Numeri
Spazio figure
Dati e previsioni
Relazioni e funzioni
Totale
Numero di domande Numero di Item1
8
12
9
11
9
16
5
14
31
53
1
Una domanda può essere composta da più item, come nel caso di domande a scelta multipla complessa del tipo Vero o Falso. L’attribuzione di un eventuale punteggio parziale sarà definita
in sede di analisi dei dati complessivi. 1
Tabella della suddivisione degli item in relazione ad ambiti e processi
Processi/Ambiti
Numeri
Spazio e
figure
Dati e Previsioni
1. Conoscere e padroneggiare i contenuti specifici della matematica (oggetti matematici, proprietà,
strutture...)
D2, D21
D11a-b
D15, D31
D6b, D12a
2. Conoscere e utilizzare algoritmi e procedure (in ambito aritmetico, geometrico...)
D28a-b
3. Conoscere diverse forme di rappresentazione e passare da una all'altra (verbale, numerica, simbolica, grafica, ...)
4. Risolvere problemi utilizzando strategie in ambiti diversi – numerico, geometrico, algebrico –
(individuare e collegare le informazioni utili, individuare e utilizzare procedure risolutive,
confrontare strategie di soluzione, descrivere e rappresentare il procedimento risolutivo,…)
5. Riconoscere in contesti diversi il carattere misurabile di oggetti e fenomeni, utilizzare strumenti
di misura, misurare grandezze, stimare misure di grandezze (individuare l'unità o lo strumento di
misura più adatto in un dato contesto, stimare una misura,…)
6. Acquisire progressivamente forme tipiche del pensiero matematico (congetturare, verificare,
giustificare, definire, generalizzare, ...)
7. Utilizzare strumenti, modelli e rappresentazioni nel trattamento quantitativo dell'informazione in
ambito scientifico, tecnologico, economico e sociale (descrivere un fenomeno in termini quantitativi, utilizzare modelli matematici per descrivere e interpretare situazioni e fenomeni, interpretare
una descrizione di un fenomeno in termini quantitativi con strumenti statistici o funzioni ...)
8. Riconoscere le forme nello spazio e utilizzarle per la risoluzione di problemi geometrici o di
modellizzazione (riconoscere forme in diverse rappresentazioni, individuare relazioni tra forme,
immagini o rappresentazioni visive, visualizzare oggetti tridimensionali a partire da una rappresentazione bidimensionale e, viceversa, rappresentare sul piano una figura solida, saper cogliere
le proprietà degli oggetti e le loro relative posizioni, …)
TOTALE
D8a-b,
D17
Relazioni e funzioni
8
D6a, D12b, D14a,
D18a-b, D23,
D25
D13b
10
D1a-d, D14b
D4a-b, D5, D13a,
D10a-d, D27a-d
17
D4c
5
D7
D16, D19,
D24
D20
D3a-c,
D29
D9a-b
3
D30
6
D22
3
D26
12
11
TOTALE
1
16
14
53
2
Di seguito viene proposta un’analisi dei quesiti utilizzando una tabella a tre colonne in cui vengono rispettivamente indicati:
 nella prima il testo del quesito. La numerazione dei quesiti fa riferimento alla versione dei fascicoli che riporta in prima pagina “Fascicolo 1”;
 nella seconda le caratteristiche facendo riferimento al Quadro di riferimento delle prove SNV pubblicato sul sito INVALSI. Nella voce “Indicazioni Nazionali e Linee
Guida” sono riportati, in parallelo, obiettivi di apprendimento presenti nelle Linee Guida per l'istruzione tecnica (riportati in carattere normale) e nelle Indicazioni
Nazionali per il sistema dei Licei (riportati in corsivo);
 nella terza una descrizione e un commento didattico; i possibili errori segnalati sono stati rilevati in sede di pretest ma ovviamente non hanno alcuna pretesa di
costituire una lista completa degli errori possibili e delle loro motivazioni.
È importante sottolineare che le caratteristiche proposte sono solo indicative e non devono rappresentare un vincolo per l'interpretazione del risultato: in matematica ogni
domanda coinvolge spesso diversi ambiti, e la risposta richiede processi di diversa natura. Seguendo la prassi internazionale, si indicano l'ambito e il processo prevalenti,
tenendo presente che spesso la scelta di un particolare distrattore può indicare difficoltà o lacune in altri ambiti o in altri processi.
La guida verrà aggiornata alla fine di luglio inserendo i risultati dell’elaborazione delle classi campione.
3
Domanda
GUIDA ALLA LETTURA
Caratteristiche
AMBITO PREVALENTE
Dati e Previsioni
SCOPO DELLA DOMANDA
Leggere un grafico per ricavarne informazioni e operare confronti.
PROCESSO PREVALENTE
Conoscere diverse forme di rappresentazione e passare da una all'altra.
Indicazioni Nazionali e Linee Guida
Dati, loro organizzazione e rappresentazione.
Raccogliere, organizzare e rappresentare un
insieme di dati.
Rappresentare e analizzare in diversi modi
(anche utilizzando strumenti informatici) un
insieme di dati, scegliendo le rappresentazioni più idonee.
Descrizione e commento
Risposta corretta: V V F V
La domanda consente di valutare competenze
di lettura di un grafico. Ai primi tre item si
può rispondere anche senza fare riferimento
ai dati numerici, rimanendo quindi all’interno
del registro di rappresentazione grafica.
L’ultimo item richiede invece una semplice
elaborazione numerica a partire dai dati letti
sul grafico e quindi richiede necessariamente
un passaggio di rappresentazioni, anche se
elementare.
4
Domanda
Caratteristiche
AMBITO PREVALENTE
Numeri
SCOPO DELLA DOMANDA
Riconoscere che la somma di due quadrati è
una quantità non negativa.
PROCESSO PREVALENTE
Conoscere e padroneggiare i contenuti specifici della matematica.
Indicazioni Nazionali e Linee Guida
Equazioni e disequazioni di primo e secondo
grado. Sistemi di equazioni e di disequazioni.
Risolvere equazioni e disequazioni di primo
e secondo grado; risolvere sistemi di
equazioni e disequazioni.
Soluzioni delle equazioni di primo grado in
una incognita, delle disequazioni associate e
dei sistemi di equazioni lineari in due
incognite, e ... tecniche necessarie alla loro
risoluzione grafica e algebrica.
Descrizione e commento
Risposta corretta: C
Gli studenti hanno a disposizione diverse
strategie per rispondere. La più semplice è
quella di osservare che la somma di un
numero reale non negativo, x2, con 1 è
sicuramente positiva in quanto non è minore
di 1. Naturalmente possono anche pensare al
grafico della funzione f(x) = x2 + 1 e
osservare che i suoi punti P(x, x2 + 1) sono
tutti situati al di sopra dell’asse delle x,
quindi per ogni x si ha x2 + 1 > 0.
Infine possono, se hanno svolto la teoria delle
disequazioni di secondo grado, osservare che
il discriminante dell’equazione associata è
negativo e quindi x2 + 1 assume, per ogni x il
segno del coefficiente di x2 , che è positivo.
In tutti i casi sono richieste competenze di
conversione da un registro di rappresentazione a un altro. Da osservare che per alcuni
studenti il segno  di “disuguaglianza larga”
potrebbe essere fonte di difficoltà. Ci sono
infatti studenti che ritengono non corretto
dire che un numero positivo sia maggiore o
uguale a 0. Freudenthal parlava, in questi
casi, della differenza tra dire la verità e dire
“tutta la verità”. In matematica ci si
accontenta di dire la verità; ed è vero che un
numero maggiore di 0 è anche maggiore o
5
Domanda
Caratteristiche
AMBITO PREVALENTE
Spazio e figure
SCOPO DELLA DOMANDA
Determinare la verità o falsità di implicazioni logiche in ambito geometrico.
PROCESSO PREVALENTE
Acquisire progressivamente forme tipiche
del pensiero matematico.
Indicazioni Nazionali e Linee Guida
Nozioni fondamentali di geometria del piano
e dello spazio.
Conoscenza dei fondamenti della geometria
euclidea del piano. Elementi della geometria
euclidea del piano e dello spazio.
Descrizione e commento
uguale a 0. È una caratteristica tipica della
razionalità matematica, ma che non verrebbe
accettata in altri contesti, per esempio in
quello giudiziario, dove ci si aspetta che il
testimone dica non solo la verità, ma tutta la
verità.
Può essere utile far riflettere gli studenti su
questi aspetti che sono particolarmente
importanti per entrare nella logica dell’argomentazione matematica.
Risposta corretta: F V V
Per rispondere correttamente gli studenti
devono non solo conoscere le proprietà del
rettangolo, del rombo e del quadrato, ma
anche riconoscere il tipo di conseguenza
logica fra le proposizioni coinvolte nel testo
dei tre item. Si tratta quindi di un quesito
utile a valutare la conoscenza di proprietà
geometriche, ma, soprattutto, la competenza
di determinare la relazione di conseguenza
logica tra due proposizioni che riguardano
proprietà note di figure geometriche.
6
Domanda
Caratteristiche
AMBITO PREVALENTE
Relazioni e funzioni
SCOPO DELLA DOMANDA
a. Completare una tabella a due colonne che
esprime la dipendenza tra due variabili.
b. Esprimere attraverso una formula la relazione tra due variabili.
c. Risolvere un problema.
PROCESSO PREVALENTE
a. e b. Conoscere diverse forme di rappresentazione e passare da una all'altra.
c. Risolvere problemi utilizzando strategie in
ambiti diversi – numerico, geometrico,
algebrico.
Indicazioni Nazionali e Linee Guida
Dati, loro organizzazione e rappresentazione.
Raccogliere, organizzare e rappresentare un
insieme di dati.
Rappresentare e analizzare in diversi modi
(anche utilizzando strumenti informatici) un
insieme di dati, scegliendo le rappresentazioni più idonee.
Descrizione e commento
Risposta corretta:
a.
T (settimane) 0 1 2 3 4 n (m3) 100 98 96 94 92 b. n = 100 – 2t.
c. B Per completare la tabella dell’item a. è
sufficiente che lo studente comprenda che
ogni settimana il serbatoio perde 2 m3 di
acqua, risultato della differenza tra i 5 m3 con
cui viene alimentato e i 7 m3 prelevati dal
villaggio. Una volta acquisita tale informazione, la compilazione della tabella avviene
interamente nel registro di rappresentazione
numerico.
L’item b. richiede invece il passaggio alla
rappresentazione simbolica.
All’item c. si può rispondere rimanendo
all’interno del registro numerico o, più velocemente, determinando lo zero della funzione
rappresentata dall’equazione
n = 100 – 2t.
7
Domanda
Caratteristiche
AMBITO PREVALENTE
Relazioni e funzioni
SCOPO DELLA DOMANDA
Associare a una formula che esprime una
funzione lineare il suo possibile grafico.
PROCESSO PREVALENTE
Conoscere diverse forme di rappresentazione e passare da una all'altra.
Indicazioni Nazionali e Linee Guida
Le funzioni e la loro rappresentazione
(numerica, funzionale, grafica).
Funzioni di vario tipo (lineari, quadratiche,
circolari, di proporzionalità diretta e inversa).
Rappresentare sul piano cartesiano le
principali funzioni incontrate.
Studiare le funzioni f(x) = ax + b e f(x) = ax2
+ bx + c.
Le funzioni del tipo f(x) = ax + b, f(x) = |x|,
f(x) = a/x, f(x) = x2 sia in termini
strettamente matematici sia in funzione della
descrizione e soluzione di problemi applicativi.
Descrizione e commento
Risposta corretta: A
L’osservazione che la pendenza della
funzione è negativa porta immediatamente
scartare i grafici B e D.
La scelta tra i grafici A e C non può essere
effettuata ricorrendo al concetto di intercetta
all’origine: per scegliere correttamente gli
studenti devono valutare la pendenza sul
grafico oppure lo zero, oppure utilizzare un
altro punto diverso da (0,1).
Si tratta quindi di una domanda che richiede
la conoscenza di diverse forme di rappresentazione (grafica e simbolica, innanzitutto, ma
anche numerica, nel calcolo della pendenza o
dell’appartenenza o meno di un punto al
grafico di una funzione) e la competenza di
passare dall’una all’altra.
8
Domanda
Caratteristiche
AMBITO PREVALENTE
Dati e Previsioni
SCOPO DELLA DOMANDA
a. Calcolare la probabilità di un evento come
rapporto tra casi favorevoli e casi possibili
b. Interpretare il significato di probabilità
PROCESSO PREVALENTE
a. Conoscere e utilizzare algoritmi e procedure
b. Conoscere e padroneggiare i contenuti
specifici della matematica
Indicazioni nazionali e Linee Guida
Significato della probabilità e sue valutazioni. Semplici spazi (discreti) di probabilità: eventi disgiunti, probabilità composta,
eventi indipendenti.
Nozione di probabilità, con esempi tratti da
contesti classici e con l’introduzione di
nozioni di statistica.
AMBITO PREVALENTE
Spazio e figure
SCOPO DELLA DOMANDA
Riconoscere un rapporto di similitudine e
applicarne le proprietà.
Descrizione e commento
Risposta corretta:
a. 12/48 o 1/4 o 0,25
b. 7
La domanda richiede il calcolo di una
probabilità mediante un semplice rapporto fra
casi favorevoli e casi possibili.
Risposta corretta: 20
Gli studenti possono rispondere utilizzando
una proporzione o, in termini equivalenti, il
rapporto di similitudine fra i due triangoli.
PROCESSO PREVALENTE
Risolvere problemi utilizzando strategie in
9
Domanda
Caratteristiche
Descrizione e commento
ambiti diversi – numerico, geometrico,
algebrico.
Indicazioni nazionali e Linee Guida
Teorema di Talete e sue conseguenze.
Similitudini con particolare riguardo al
teorema di Talete.
AMBITO PREVALENTE
Numeri
SCOPO DELLA DOMANDA
a. Utilizzare una regola espressa nel linguaggio naturale (piano tariffario) per
calcolare il costo di una telefonata.
b. Ricavare la durata di una telefonata a
partire dal piano tariffario e dal credito
residuo.
PROCESSO PREVALENTE
Risolvere problemi utilizzando strategie in
ambiti diversi – numerico, geometrico,
algebrico.
Risposta corretta:
a. 1,11 euro
b. 32 minuti
Gli studenti possono rispondere rimanendo
sempre all’interno del registro di rappresentazione numerico, oppure determinando una
formula per la funzione che esprime il costo
di una telefonata in funzione del tempo.
In questo secondo caso, per rispondere
all’item a. devono calcolare l’output della
funzione corrispondente a un determinato
input. Per rispondere all’item b. devono fare
il procedimento inverso: noto l’output
devono calcolare il corrispondente input.
Indicazioni nazionali e Linee Guida
Le operazioni con i numeri interi e razionali.
Operare con i numeri interi e razionali e
valutare l’ordine di grandezza dei risultati.
Calcolo (mentale, con carta e penna, mediante strumenti) con i numeri interi, con i
numeri razionali sia nella scrittura come
10
Domanda
Caratteristiche
frazione che nella rappresentazione decimale.
Le funzioni e la loro rappresentazione (numerica, funzionale, grafica).
Funzioni lineari.
AMBITO PREVALENTE
Numeri
SCOPO DELLA DOMANDA
a. Leggere i valori di una distribuzione di
frequenza in cui le classi sono intervalli.
b. Determinare i valori percentuali di una
distribuzione di frequenza in cui le classi
sono intervalli.
PROCESSO PREVALENTE
Utilizzare strumenti, modelli e rappresentazioni nel trattamento quantitativo dell'informazione in ambito scientifico, tecnologico, economico e sociale.
Descrizione e commento
Risposta corretta:
a. 10
b. D
Per rispondere all’item a. è sufficiente saper
leggere una distribuzione di frequenza
rappresentata in una tabella e calcolare un
valore della sua cumulata.
Per rispondere all’item b. è sufficiente il
calcolo di una percentuale o il passaggio alla
distribuzione di frequenza percentuale e poi il
calcolo di un valore della sua cumulata.
Indicazioni Nazionali e Linee Guida
Distribuzioni delle frequenze a seconda del
tipo di carattere e principali rappresentazioni
grafiche.
Distinguere tra caratteri qualitativi, quantitativi discreti e quantitativi continui, operare con distribuzioni di frequenze e rappresentarle.
11
Domanda
Caratteristiche
AMBITO PREVALENTE
Relazioni e funzioni
SCOPO DELLA DOMANDA
a. b. c. d. Utilizzare diverse rappresentazioni
(grafici e formule) per determinare zeri,
segni e confronti di funzioni lineari.
PROCESSO PREVALENTE
Conoscere diverse forme di rappresentazione e passare da una all'altra.
Indicazioni Nazionali e Linee Guida
Il metodo delle coordinate: il piano cartesiano.
Il metodo delle coordinate cartesiane,...
rappresentazione di punti e rette nel piano e
di proprietà come il parallelismo e la
perpendicolarità.
Le funzioni e la loro rappresentazione
(numerica, funzionale, grafica).
Funzioni lineari.
Descrizione e commento
Risposta corretta: V F V V
Per rispondere all’item a. gli studenti
possono aiutarsi con la rappresentazione
grafica: 1,2 è un valore plausibile dell’input
che rende uguali f(x) e g(x). Per verificare
che f(1,2) = g(1,2) è sufficiente calcolare
f(1,2) e g(1,2) e verificare che sono uguali. Si
tratta dell’unico valore perché le due funzioni
sono lineari e hanno diversa pendenza.
Per rispondere all’item b. è sufficiente osservare il grafico di f, oppure determinare un
qualunque controesempio.
Anche all’item c. è possibile rispondere
aiutandosi con il grafico: 2,5 è un valore
plausibile per il grafico di f. Sostituendo si
trova che f(2,5) = 0.
All’item d. si può rispondere osservando il
grafico, dopo avere determinato che f(1,2) =
g(1,2).
Naturalmente si sarebbe potuto rispondere a
tutti gli item utilizzando unicamente il registro di rappresentazione simbolico.
12
Domanda
Caratteristiche
AMBITO PREVALENTE
Numeri
SCOPO DELLA DOMANDA
Capire se lo studente ha chiara la definizione
del numero π come rapporto tra la lunghezza
di una circonferenza e il suo diametro.
PROCESSO PREVALENTE
Conoscere e padroneggiare i contenuti specifici della matematica.
Descrizione e commento
Risposta corretta:
a. B
b. D
I due item valutano pure conoscenze: il
primo la definizione di  come rapporto fra la
lunghezza di una circonferenza e il suo diametro; il secondo riguarda la rappresentazione decimale di un numero irrazionale.
Indicazioni Nazionali e Linee Guida
I numeri: naturali, interi, razionali, sotto
forma frazionaria e decimale, irrazionali e,
in forma intuitiva, reali.
Conoscenza intuitiva dei numeri reali, con
particolare riferimento alla loro rappresentazione geometrica su una retta.
Nozioni fondamentali di geometria del piano
e dello spazio.
Conoscenza dei fondamenti della geometria
euclidea del piano. Elementi della geometria
euclidea del piano e dello spazio.
13
Domanda
Caratteristiche
AMBITO PREVALENTE
Dati e Previsioni
SCOPO DELLA DOMANDA
a. Leggere i dati in una tabella per
individuare la differenza tra il massimo e il
minimo.
b. Calcolare la media aritmetica dei dati di
una tabella.
PROCESSO PREVALENTE
a. Conoscere e padroneggiare i contenuti
specifici della matematica.
b. Conoscere e utilizzare algoritmi e procedure.
Descrizione e commento
Risposta corretta:
a. 11°C
b. TM = -5°C
Il primo item valuta la capacità di leggere
una tabella e di comprendere un testo: il
calcolo richiesto è molto semplice, anche se
comporta la sottrazione tra un numero positivo e uno negativo.
Il secondo item richiede il calcolo della media aritmetica di un insieme di otto dati.
Indicazioni Nazionali e Linee Guida
Valori medi e misure di variabilità.
Calcolare i valori medi e alcune misure di
variabilità di una distribuzione.
Definizioni e proprietà dei valori medi e
delle misure di variabilità, nonché uso
strumenti di calcolo (calcolatrice, foglio di
calcolo) per analizzare raccolte di dati e
serie statistiche
14
Domanda
Caratteristiche
AMBITO PREVALENTE
Relazioni e funzioni
SCOPO DELLA DOMANDA
a. Passare dal registro verbale a quello simbolico e individuare l'equazione che calcola
una lunghezza.
b. Risolvere un'equazione di primo grado
con coefficienti razionali.
PROCESSO PREVALENTE
a. Conoscere diverse forme di rappresentazione e passare da una all'altra
b. Conoscere e utilizzare algoritmi e procedure.
Indicazioni Nazionali e Linee Guida
Equazioni e disequazioni di primo e secondo
grado. Sistemi di equazioni e di disequazioni.
Risolvere equazioni e disequazioni di primo
e secondo grado; risolvere sistemi di
equazioni e disequazioni.
Soluzioni delle equazioni di primo grado in
una incognita, delle disequazioni associate e
dei sistemi di equazioni lineari in due
incognite, e ... tecniche necessarie alla loro
risoluzione grafica e algebrica.
Descrivere un problema con un’equazione,
una disequazione o un sistema di equazioni
o disequazioni.
Descrizione e commento
Risposta corretta:
a. D
b. Lo studente
l’equazione
risolve
correttamente
1
1
x  x  8,9  x
5
6
Si accetta un qualunque risultato compreso
tra 14 e 14,8, estremi inclusi espresso in
qualunque forma, anche lasciando il calcolo
incompiuto (x = 8,9 ∙ 30/19 )
Il primo item richiede di riconoscere, fra
diverse equazioni date, quella che rappresenta il problema posto. Nell’item b. si chiede
invece di determinare la lunghezza totale del
palo, cioè la soluzione dell’equazione.
Potrebbe sembrare che i due item siano
fortemente dipendenti l’uno dall’altro, ma
non è così, perché per rispondere al secondo
item possono essere utilizzate diverse strategie che non necessariamente portano a formalizzare il problema con l’equazione D.
15
Domanda
Caratteristiche
AMBITO PREVALENTE
Dati e Previsioni
SCOPO DELLA DOMANDA
a. Calcolare una percentuale
b. Mettere in corrispondenza dati organizzati
in tabella con un grafico a settori circolari
Descrizione e commento
Risposta corretta:
a. 49%
b. PROCESSO PREVALENTE
a. Conoscere e utilizzare algoritmi e procedure
b. Conoscere diverse forme di rappresentazione e passare da una all'altra
Indicazioni Nazionali e Linee Guida
Distribuzioni delle frequenze a seconda del
tipo di carattere e principali rappresentazioni
grafiche.
Distinguere tra caratteri qualitativi, quantitativi discreti e quantitativi continui, operare con distribuzioni di frequenze e rappresentarle.
Dati, loro organizzazione e rappresentazione.
Raccogliere, organizzare e rappresentare un
insieme di dati.
Rappresentare e analizzare in diversi modi
(anche utilizzando strumenti informatici) un
insieme di dati, scegliendo le rappresentazioni più idonee
Il primo item richiede la lettura di una
distribuzione di frequenze rappresentata in
una tabella e il calcolo di una percentuale o il
passaggio alla distribuzione di frequenze
percentuali e il successivo calcolo di un valore della sua cumulata.
Il secondo item sonda invece la competenza
di passare da un registro di rappresentazione
numerico (la tabella e i suoi valori) a un
registro di rappresentazione grafica (il grafico a settori circolari).
16
Domanda
Caratteristiche
AMBITO PREVALENTE
Spazio e figure
SCOPO DELLA DOMANDA
Conoscere la condizione di parallelismo tra
rette.
PROCESSO PREVALENTE
Conoscere e padroneggiare i contenuti
specifici della matematica.
Indicazioni Nazionali e Linee Guida
Il metodo delle coordinate: il piano
cartesiano.
Il metodo delle coordinate cartesiane,...
rappresentazione di punti e rette nel piano e
di proprietà come il parallelismo e la
perpendicolarità.
AMBITO PREVALENTE
Spazio e figure
SCOPO DELLA DOMANDA
Calcolare il rapporto tra i volumi di due
figure simili conoscendo il rapporto di
similitudine.
Descrizione e commento
Risposta corretta: D
Per rispondere gli studenti devono sapere che
le due rette che rappresentano due funzioni
lineari di uguale pendenza sono parallele. A
questo punto devono risolvere l’equazione
k/2 = 3 , ottenendo k = 6.
Risposta corretta: D
La domanda consente di valutare una
conoscenza particolarmente importante: qual
è il rapporto tra i volumi di due figure simili
e di cui è noto il rapporto di similitudine. PROCESSO PREVALENTE
Riconoscere in contesti diversi il carattere
misurabile di oggetti e fenomeni, utilizzare
strumenti di misura, misurare grandezze,
stimare misure di grandezze.
17
Domanda
Caratteristiche
Indicazioni Nazionali e Linee Guida
Nozioni fondamentali di geometria del piano
e dello spazio.
Conoscenza dei fondamenti della geometria
euclidea del piano. Elementi della geometria
euclidea del piano e dello spazio.
AMBITO PREVALENTE
Numeri
SCOPO DELLA DOMANDA
Risolvere un problema e interpretare il
risultato rispetto alla situazione reale
PROCESSO PREVALENTE
Risolvere problemi utilizzando strategie in
ambiti diversi – numerico, geometrico,
algebrico.
Descrizione e commento
Risposta corretta: 11
Si tratta di un semplice problema in cui deve
essere effettuato un controllo di plausibilità e
coerenza del risultato ottenuto con la
situazione reale. Non sono infatti state
accettate risposte come 11,25 o “circa 11”.
Indicazioni Nazionali e Linee Guida
Le operazioni con i numeri interi e razionali.
Operare con i numeri interi e razionali e
valutare l’ordine di grandezza dei risultati.
Calcolo (mentale, con carta e penna,
mediante strumenti) con i numeri interi, con
i numeri razionali sia nella scrittura come
frazione che nella rappresentazione decimale.
18
Domanda
Caratteristiche
AMBITO PREVALENTE
Dati e Previsioni
SCOPO DELLA DOMANDA
a. Calcolare la probabilità dell’evento contrario.
b. Calcolare la probabilità dell’evento congiunto.
PROCESSO PREVALENTE
Conoscere e utilizzare algoritmi e procedure.
Indicazioni Nazionali e Linee Guida
Significato della probabilità e sue valutazioni. Semplici spazi (discreti) di probabilità: eventi disgiunti, probabilità composta,
eventi indipendenti.
Nozione di probabilità, con esempi tratti da
contesti classici e con l’introduzione di
nozioni di statistica.
Descrizione e commento
Risposta corretta:
a. 93%
b. B
Nel primo item si tratta di calcolare la probabilità dell’evento contrario.
Nel secondo item bisogna calcolare la probabilità di due eventi indipendenti congiunti.
Una piccola difficoltà in più può essere data
dal calcolo del prodotto di due percentuali:
2% . 7% deve essere interpretato come 2/100
.
7/100. Si ottiene quindi 0,0014 = 0,14%
19
Domanda
Caratteristiche
AMBITO PREVALENTE
Spazio e figure
SCOPO DELLA DOMANDA
Sapere calcolare l’area di un poligono “non
standard” nel piano cartesiano utilizzando
l'equiscomponibilità.
PROCESSO PREVALENTE
Riconoscere in contesti diversi il carattere
misurabile di oggetti e fenomeni, utilizzare
strumenti di misura, misurare grandezze,
stimare misure di grandezze.
Indicazioni Nazionali e Linee Guida
Nozioni fondamentali di geometria del piano
e dello spazio.
Conoscenza dei fondamenti della geometria
euclidea del piano. Elementi della geometria
euclidea del piano e dello spazio.
Descrizione e commento
Risposta corretta:
9 cm2
Spesso nei test INVALSI compaiono domande di questo tipo. In questi casi il calcolo delle aree può essere effettuato per composizione o scomposizione di figure.
Qui è più semplice calcolare l’area del
quadrilatero ABCD come somma delle aree
dei triangoli ABD e BDC, quindi come
0,5(3.4) + 0,5(3.2) = 6 + 3 = 9 m2.
Spesso gli studenti si trovano in difficoltà di
fronte a quesiti simili, che dovrebbero essere
abituati ad affrontare già dalla scuola secondaria di primo grado.
20
Domanda
Caratteristiche
AMBITO PREVALENTE
Numeri
SCOPO DELLA DOMANDA
Trovare un controesempio a un'affermazione
algebrica.
PROCESSO PREVALENTE
Acquisire progressivamente forme tipiche
del pensiero matematico.
Indicazioni Nazionali e Linee Guida
Equazioni e disequazioni di primo e secondo
grado. Sistemi di equazioni e di disequazioni.
Risolvere equazioni e disequazioni di primo
e secondo grado; risolvere sistemi di equazioni e disequazioni.
Soluzioni delle equazioni di primo grado in
una incognita, delle disequazioni associate e
dei sistemi di equazioni lineari in due incognite, e ... tecniche necessarie alla loro
risoluzione grafica e algebrica.
Descrizione e commento
Risposta corretta:
Lorenza non ha ragione, perché …… i
numeri reali comprendono anche i numeri
negativi
O qualsiasi controesempio corretto
O un qualunque calcolo che mostri che la
disequazione data è equivalente a x > 0.
In questo caso la risposta più economica e
chiara sarebbe l’esibizione di un controesempio. Per esempio, se x =–1, la disuguaglianza è falsa. Poiché la proposizione riguarda una totalità di oggetti (è quantificata universalmente) è sufficiente far vedere che cade
in difetto su un unico esempio per dichiararla
falsa. Naturalmente si accettano anche risposte che dimostrino che la disuguaglianza non
è verificata per alcun numero negativo, però
sarebbe bene discutere con gli studenti che
hanno scelto tale giustificazione come sia
molto meno elegante, economica e chiara di
quella in cui si esibisce un controesempio.
Anche queste discussioni contribuiscono ad
avvicinare gli studenti alla razionalità matematica, che non è naturale, ma va introdotta
gradualmente e sistematicamente.
21
Domanda
Caratteristiche
AMBITO PREVALENTE
Numeri
SCOPO DELLA DOMANDA
Utilizzare le proprietà delle potenze e la
proprietà distributiva per manipolare
un'espressione algebrica.
PROCESSO PREVALENTE
Conoscere e padroneggiare i contenuti
specifici della matematica.
Indicazioni Nazionali e Linee Guida
Le espressioni letterali e i polinomi.
Padroneggiare l’uso della lettera come mero
simbolo e come variabile.
Elementi di base del calcolo letterale.
Calcoli con le espressioni letterali sia per
rappresentare un problema (mediante
un’equazione, disequazioni o sistemi) e
risolverlo, sia per dimostrare risultati generali, in particolare in aritmetica.
AMBITO PREVALENTE
Dati e Previsioni
SCOPO DELLA DOMANDA
Calcolare la probabilità di un evento
riconoscendo nel contesto gli eventi
favorevoli e quelli possibili
Descrizione e commento
Risposta corretta:
B
Si può rispondere lavorando solo sul piano
sintattico, applicando la proprietà distributiva
e le proprietà delle potenze, o si può lavorare
sul piano semantico, osservando che l’ordine
di grandezza di a43 + a44 non può essere
rappresentato da nessuna delle risposte A, C
o D..
Può essere interessante discutere in classe dei
punti di forza e di debolezza delle due
strategie per ottenere la risposta corretta.
Risposta corretta: 15/38
Si tratta di un semplice calcolo di probabilità
come rapporto tra casi favorevoli e casi
possibili, osservando che gli eventi sono
dipendenti.
PROCESSO PREVALENTE
22
Domanda
Caratteristiche
Descrizione e commento
Utilizzare strumenti, modelli e rappresentazioni nel trattamento quantitativo dell'informazione in ambito scientifico, tecnologico, economico e sociale.
Indicazioni Nazionali e Linee Guida
Significato della probabilità e sue valutazioni. Semplici spazi (discreti) di probabilità: eventi disgiunti, probabilità composta,
eventi indipendenti.
Nozione di probabilità, con esempi tratti da
contesti classici e con l’introduzione di
nozioni di statistica.
AMBITO PREVALENTE
Dati e Previsioni
SCOPO DELLA DOMANDA
Calcolare una media pesata.
PROCESSO PREVALENTE
Conoscere e utilizzare algoritmi e procedure.
Indicazioni nazionali e Linee Guida
Valori medi e misure di variabilità.
Calcolare i valori medi e alcune misure di
variabilità di una distribuzione.
Definizioni e proprietà dei valori medi e
delle misure di variabilità, nonché uso
strumenti di calcolo (calcolatrice, foglio di
calcolo) per analizzare raccolte di dati e
serie statistiche.
Risposta corretta:
(20∙85+80∙65)/100
Risultato: 69
È importante che gli studenti si accorgano
che viene richiesta loro una media pesata.
Una volta che sia stato compreso questo fatto
il calcolo della media aritmetica è molto
semplice.
23
Domanda
Caratteristiche
AMBITO PREVALENTE
Spazio e figure
SCOPO DELLA DOMANDA
Stimare il volume di un cilindro.
PROCESSO PREVALENTE
Riconoscere in contesti diversi il carattere
misurabile di oggetti e fenomeni, utilizzare
strumenti di misura, misurare grandezze,
stimare misure di grandezze.
Indicazioni Nazionali e Linee Guida
Nozioni fondamentali di geometria del piano
e dello spazio.
Conoscenza dei fondamenti della geometria
euclidea del piano. Elementi della geometria
euclidea del piano e dello spazio.
AMBITO REVALENTE
Dati e Previsioni
SCOPO DELLA DOMANDA
Conoscere ed applicare la legge empirica del
caso per la stima di una frequenza.
PROCESSO PREVALENTE
Conoscere e utilizzare algoritmi e procedure.
Descrizione e commento
Risposta corretta:
B
La domanda valuta capacità di stima di
confronto di grandezze. Gli studenti devono
sapere che la capacità è una misura di volume
e come si passa dai cm3 ai litri o viceversa.
Risposta corretta:
A
La domanda consente di valutare quanto sia
stata compresa la legge empirica del caso e
quanto uno studente sia in grado di applicarla
per effettuare stime in condizioni di incertezza.
Indicazioni Nazionali e Linee Guida
Significato della probabilità e sue valutazioni. Semplici spazi (discreti) di probabilità: eventi disgiunti, probabilità composta,
24
Domanda
Caratteristiche
eventi indipendenti.
Nozione di probabilità, con esempi tratti da
contesti classici e con l’introduzione di
nozioni di statistica.
AMBITO PREVALENTE
Spazio e figure
SCOPO DELLA DOMANDA
Riconoscere il solido ottenuto da una
rotazione di una figura piana.
Descrizione e commento
Risposta corretta:
D
Si tratta di una domanda che richiede
competenze di visualizzazione nello spazio.
PROCESSO PREVALENTE
Riconoscere le forme nello spazio e
utilizzarle per la risoluzione di problemi
geometrici o di modellizzazione.
Indicazioni Nazionali e Linee Guida
Nozioni fondamentali di geometria del piano
e dello spazio.
Conoscenza dei fondamenti della geometria
euclidea del piano. Elementi della geometria
euclidea del piano e dello spazio.
25
Domanda
Caratteristiche
AMBITO PREVALENTE
Relazioni e funzioni
SCOPO DELLA DOMANDA
Confrontare i registri verbale e grafico e
ricavare informazioni da entrambi.
PROCESSO PREVALENTE
Conoscere diverse forme di rappresentazione e passare da una all'altra.
Indicazioni Nazionali e Linee Guida
Le funzioni e la loro rappresentazione (numerica, funzionale, grafica).
Funzioni di vario tipo (lineari, quadratiche,
circolari, di proporzionalità diretta e inversa).
Rappresentare sul piano cartesiano le
principali funzioni incontrate.
Studiare le funzioni f(x) = ax + b e f(x) = ax2
+ bx + c.
Le funzioni del tipo f(x) = ax + b, f(x) = |x|,
f(x) = a/x, f(x) = x2 sia in termini
strettamente matematici sia in funzione della
descrizione e soluzione di problemi applicativi.
Descrizione e commento
Risposta corretta:
V F V F
Gli studenti, per rispondere, devono saper
leggere e interpretare un grafico posizionetempo di un oggetto che si muove su una
traiettoria rettilinea.
I primi due item richiedono solo la competenza di interpretare le informazioni scritte
sui due assi, indipendentemente l’uno dall’altro. Il terzo e il quarto item richiedono
invece una lettura coordinata delle due
variazioni (posizioni e istanti di tempo),
quindi una lettura “funzionale” del grafico. In
particolare hanno a che fare con l’interpretazione della velocità, in un diagramma
posizione-tempo formato da tratti rettilinei,
come la pendenza dei vari segmenti che
compongono il grafico.
26
Domanda
Caratteristiche
AMBITO PREVALENTE
Numeri
SCOPO DELLA DOMANDA
a. Calcolare una percentuale
b. Applicare un ragionamento proporzionale
per risolvere un problema.
Descrizione e commento
Risposta corretta:
a. A
b. A
L’item a. richiede il semplice calcolo di una
percentuale, mentre il b. è un semplice
problema di proporzionalità.
PROCESSO PREVALENTE
Conoscere e utilizzare algoritmi e procedure.
Indicazioni Nazionali e Linee Guida
Rapporti e percentuali.
Proporzionalità diretta e inversa.
27
Domanda
Caratteristiche
AMBITO PREVALENTE
Spazio e figure
SCOPO DELLA DOMANDA
Riconoscere la verità di una proposizione
quantificata nel contesto delle proprietà di
simmetria dei triangoli.
PROCESSO PREVALENTE
Acquisire progressivamente forme tipiche
del pensiero matematico.
Indicazioni nazionali e Linee Guida
Le principali trasformazioni geometriche e
loro invarianti (isometrie e similitudini).
Esempi di utilizzazione [delle trasformazioni
geometriche e degli invarianti] nella
dimostrazione di proprietà geometriche.
Le principali trasformazioni geometriche
(traslazioni, rotazioni, simmetrie, similitudini con particolare riguardo al teorema di
Talete) e le principali proprietà invarianti.
Descrizione e commento
Risposta corretta: D
Si tratta di proposizioni che richiedono la
conoscenza delle proprietà delle figure
geometriche interessate: triangoli e, in particolare, triangoli equilateri. La domanda è
resa più difficile dalla presenza, in ogni
proposizione di quantificatori. La conoscenza
delle proprietà delle figure geometriche coinvolte non sono quindi sufficienti a rispondere. È necessario possedere una discreta
capacità di gestire correttamente, sul piano
linguistico e logico, i quantificatori.
28
Domanda
Caratteristiche
AMBITO PREVALENTE
Dati e Previsioni
SCOPO DELLA DOMANDA
Riconoscere una corretta procedura di
campionamento casuale.
PROCESSO PREVALENTE
Acquisire progressivamente forme tipiche
del pensiero matematico.
Indicazioni Nazionali e Linee Guida
Dati, loro organizzazione e rappresentazione.
Raccogliere, organizzare e rappresentare un
insieme di dati.
Rappresentare e analizzare in diversi modi
(anche utilizzando strumenti informatici) un
insieme di dati, scegliendo le rappresentazioni più idonee.
Descrizione e commento
Risposta corretta:
C
La domanda ha a che fare con le conoscenze
relative alle caratteristiche che deve avere un
buon campione casuale, per consentire previsioni corrette sul comportamento dell’intera
popolazione.
Le scelte diverse da quella di Carlotta non
garantiscono, sulla base delle sole informazioni fornite, l’omogeneità del campione
rispetto alla popolazione e sono quindi da
rifiutare.
29
Domanda
Caratteristiche
AMBITO PREVALENTE
Spazio e figure
SCOPO DELLA DOMANDA
Conoscere le proprietà del triangolo e del
quadrato.
Descrizione e commento
Risposta corretta: AD, DC, CB, AE, EB
Rispondere correttamente richiede alcune
deduzioni locali sulla congruenza dei
segmenti interessati.
PROCESSO PREVALENTE
Conoscere e padroneggiare i contenuti
specifici della matematica.
Indicazioni Nazionali e Linee Guida
Nozioni fondamentali di geometria del piano
e dello spazio.
Conoscenza dei fondamenti della geometria
euclidea del piano. Elementi della geometria
euclidea del piano e dello spazio.
30