cliccare qui - Sezione di Fisica

Università di Udine – Facoltà di Scienze Matematiche, Fisiche e Naturali
FISICA MODERNA
per allievi di Matematica, Fisica Computazionale e Informatica (De Angelis)
Appunti per il corso dell’A.A. 2002/2003 – Bozza 2.2 del 25/11/02
www.fisica.uniud.it/~deangeli/fismod/corsofismod.html
1) Le origini della Fisica Quantistica
- Aspetti corpuscolari della radiazione
- Aspetti ondulatori delle particelle
2) Funzione d’onda ed equazione di Schrödinger
- Potenziali lineari a tratti; barriere di potenziale ed effetto tunnel
- Principio d’indeterminazione di Heisenberg
- Sistemi conservativi nell’intorno di una posizione di equilibrio stabile
3) Atomi
- Potenziali a simmetria sferica
- L’atomo d’idrogeno
- Spin e principio di Pauli
- Atomi a più elettroni: cenni sulla tavola periodica
4) Statistiche quantistiche
- Bose-Einstein (bosoni)
- Fermi-Dirac (fermioni); meccanismi di conduzione
5) Cenni sulla meccanica quantistica in un quadro formale (fisici e matematici) o
Cenni sui dispositivi a semiconduttore (informatici e ingegneri)
6) Teoria della relatività speciale
- Invarianza dell’intervallo spaziotemporale e trasformazioni di Lorentz
- Dinamica relativistica
- Formulazione covariante della teoria elettromagnetica
Capitolo 1
Le origini della sica quantistica
Il mondo era così recente che molte cose
erano prive di nome, e per citarle bisognava
indicarle col dito.
fuori dal visibile. Infatti un qualunque corpo a una
qualunque temperatura
T >0
emette radiazione.
La teoria elettromagnetica classica consente di
calcolare la radiazione emessa da un emettitore e
Gabriel Garcia Márquez
Cent'anni di solitudine
assorbitore perfetto (corpo nero). Un foro in una
cavità è ad esempio con buona approssimazione un
corpo nero:
la radiazione che entra nel foro può
uscirne con probabilità bassa.
Raileigh e Jeans descrissero la distribuzione di
Alla ne del secolo scorso era opinione generale
intensità
I
delle onde emesse in funzione della lun-
che la meccanica newtoniana e la teoria di Maxwell
ghezza d'onda
dell'elettromagnetismo spiegassero tutta la realtà
nero come quella proveniente da un insieme di oscil-
sica. Gli enti sici venivano ricondotti a due rap-
latori che possono emettere e assorbire radiazione
presentazioni: particelle e onde. Alcuni esperimen-
a ogni frequenza. L'espressione ottenuta
λ
modellando la radiazione di corpo
ti indicarono tuttavia fenomeni dicili da inquadrare nei modelli conosciuti: in particolare eviden-
dI/dλ = 2πc
ze sperimentali puntavano verso il fatto che alcu-
kB T
λ4
(1.1)
ni sistemi sici possono assumere solo livelli ben
(dove
deniti (quantizzati) di energia, che la descrizione
della luce) diverge per
corpuscolare è talora inadeguata a rappresentare il
letta):
comportamento delle particelle, e che la descrizione
frequenze (apparendo blu) e perdere rapidamente
ondulatoria è talora inadeguata a rappresentare il
tutta la loro energia.
comportamento della radiazione.
L'esposizione in questo capitolo
non rispecchia la
storia della sica.
kB
è la costante di Boltzmann e
λ→0
c è la velocità
(catastrofe ultravio-
tutti i corpi dovrebbero emettere ad alte
Le osservazioni sperimentali erano in contrasto
con il calcolo classico (Figura 1.1). Tali osservazioni
erano descritte dalle seguenti leggi:
1. Legge di Stefan-Boltzmann: l'intensità totale
1.1
La radiazione di corpo nero
emessa per unità di tempo vale
I = σT 4
Una delle eccezioni al successo della teoria ondula-
σ 5.7 × 10−8
2 4
W/(m K ).
toria era associata al calcolo della radiazione emes-
con
sa da un corpo a una determinata temperatura
invece, l'integrale della (1.1) diverge.
T.
Constatiamo l'emissione di radiazione da parte di
corpi ogni giorno: il sole, il lamento di una lampadina percorsa da corrente - ma anche il lamento di
una lampadina non percorso da corrente, ancorché
Si noti che,
2. Legge di Wien: lo spettro di emissione ha un
massimo nella lunghezza d'onda
λMAX =
2.9µm
T /1000K
1.2 Proprietà corpuscolari della radiazione
2
Figura 1.2: Apparato sperimentale per evidenziare
Figura 1.1: Radiazione di corpo nero.
l'eetto fotoelettrico.
(ad esempio approssimando il sole con un assorbitore perfetto si ha
T 6000
K). Si noti
che, invece, la (1.1) non ha massimo.
si noti che l'espressione di Planck tende all'espressione di Raileigh e Jeans nei limiti per
per
h → 0.
λ → ∞
e
Il calcolo classico di Raileigh e Jeans riproduce i
Era sensazione generale tuttavia che le ipotesi
dati sperimentali solo per grandi lunghezze d'onda.
di Planck fossero solo un articio matematico per
Nel 1900 Planck propose una teoria della radia-
risolvere il problema.
zione di corpo nero che riproduceva i dati sperimentali a tutte le lunghezze d'onda.
In questa teoria
le molecole non possono avere energie arbitrarie,
quantizzate,
ma al contrario le energie sono
ossia
possono avere solo valori discreti.
1.2
Proprietà corpuscolari della radiazione
1.2.1 L'eetto fotoelettrico
E = nhf
Quando una supercie metallica viene colpita da
dove
f
è la frequenza di vibrazione,
positivo e
hè
n
è un intero
radiazioni di frequenza sucientemente alta essa
una costante, oggi chiamata costante
libera elettroni; anche in assenza di dierenza di
di Planck. Inoltre postulò che quando una molecola
potenziale
passa da uno stato di energia più alta a uno di
corrente nell'apparato di Figura 1.2. È quindi plau-
energia più bassa essa emette un
sibile che la luce provochi l'emissione di elettroni
quanto di energia
V
applicata si può quindi misurare una
dal catodo.
E = h ∆n f .
Questo
Con questi postulati, l'espressione ottenuta per la
radiazione di corpo nero è
fenomeno,
noto
all'inizio
del
secolo,
si manifesta con caratteristiche inspiegabili dalla
sica classica. In particolare:
1. L'emissione, se avviene, è istantanea e il tem-
1
dI
hc
= 2πc 5 hc/λk T
.
B
dλ
λ e
−1
po di risposta non dipende dall'intensità
I
del-
la radiazione (qualora l'emissione avvenga l'intensità della corrente è proporzionale all'inten-
Per
h 6.6 × 10
−34
sità della radiazione incidente, in accordo con
Js
i dati sperimentali sono ben riprodotti.
Planck
quindi poteva spiegare la radiazione di corpo nero;
quanto atteso in base a ragionamenti classici).
2. Se la frequenza viene mantenuta costante e
V
1.2 Proprietà corpuscolari della radiazione
3
è diretto in modo tale da opporsi al usso, la
corrente si annulla per un valore del potenziale
V = −Vs ; Vs ,
I.
dipende da
detto potenziale di arresto, non
L'energia cinetica degli elettroni
emessi dipende dalla frequenza della radiazione
incidente e non dalla sua intensità.
3. L'emissione avviene solo se la luce ha frequenza
maggiore di una certa frequenza di soglia
f0 ,
e il potenziale d'arresto è legato alla frequenza
dalla relazione
eVs = h(f − f0 ) .
La spiegazione di questo fenomeno sta nel fatto
che l'energia della radiazione incidente si trasforma
in energia cinetica degli elettroni scatterati, che in
conseguenza si muovono. Non sempre però essi si
staccano dalle proprie orbite, in quanto l'energia cinetica deve essere superiore all'opposto dell'energia
totale (negativa) che tiene legati gli elettroni all'atomo.
Questo valore energetico è il potenziale di
arresto, e dipende dal tipo di metallo usato come
catodo; tipicamente vale 4-5 V.
Einstein suppose che l'energia dell'onda incidente fosse concentrata in pacchetti discreti, chiamati
fotoni, ciascuno di energia
E = hf .
Quindi, se l'energia di legame degli elettroni degli
strati più esterni vale
−E0 ,
l'energia cinetica
EK
acquistata dagli elettroni estratti vale:
EK = hf − E0 (EK > E0 ) .
L'intensità della radiazione incidente determina
Figura 1.3: Alto: Dipendenza della corrente dalla
dierenza di potenziale applicata V. Basso: dipendenza del potenziale di arresto dalla frequenza della
luce
f.
invece il numero degli elettroni destinati ad uscire
dall'orbita: più sono i fotoni incidenti maggiore è il
numero di elettroni con cui essi interagiranno.
Numerose sono le applicazioni pratiche dell'eetto fotoelettrico: ad esempio celle fotoelettriche nel
televisore, nel cinema sonoro, nelle macchine fotograche e in generale negli strumenti mediante i
quali si vuole evidenziare mediante un impulso di
corrente una variazione di un eetto luminoso.
1.2.2 L'eetto Compton
monocromatica, ad esempio un fascio di raggi X, in
seguito all'attraversamento di una sottile lamina,
per esempio di grate. La lunghezza d'onda della
radiazione diusa dalla lamina risulta essere maggiore di quella della radiazione incidente (e quindi
si verica una diminuzione della frequenza), e la
variazione di lunghezza d'onda dipende dall'angolo
di deviazione (Figura 1.5).
Questa situazione sperimentale andava a scontrarsi con la teoria della sica classica secondo la
Nel 1922 Compton mise in luce il problema del cam-
quale ogni volta che la radiazione elettromagnetica
biamento della lunghezza d'onda di una radiazione
interagisce con una particella carica, la radiazio-
1.3 Proprietà ondulatorie della materia
4
zione fosse stata trasmessa agli elettroni più esterni della lamina, permettendo ad essi di sganciarsi
dalla grate.
Il collegamento con la teoria dei quanti consiste
hf
nel fatto che il fotone ha un'energia
proporzio-
nale alla frequenza; nell'interazione con l'elettrone
esso perde parte dell'energia (e quindi la sua lunghezza d'onda aumenta).
chiamo con
φ
In particolare, se indi-
l'angolo di diusione del fotone dopo
l'urto con l'elettrone e con
∆λ
la dierenza tra la
lunghezza d'onda del fotone prima e dopo l'urto
si può calcolare (faremo questo calcolo dopo avere
introdotto la teoria della relatività speciale) che:
Figura 1.4:
Schema del processo di scattering
∆λ =
Compton.
dove
c
h
(1 − cos φ)
me c
è la velocità della luce,
Planck e
me
h
la costante di
la massa dell'elettrone.
Il risultato
spiega i dati sperimentali.
h/mc
La quantità
viene
chiamata lunghezza
d'onda Compton di una particella di massa
m;
per
l'elettrone ha valore di circa 2.4 pm.
1.3
Proprietà ondulatorie della
materia
Se la luce può avere manifestazioni corpuscolari,
è ragionevole pensare che a loro volta le particelle siano soggette a fenomeni per spiegare i quali è
necessario invocare la meccanica ondulatoria.
1.3.1 Relazione di de Broglie
Ciò infatti si verica sperimentalmente: in particolare, gli elettroni sono soggetti a fenomeni di dirazione così come le onde classiche. In tali fenomeni
Figura 1.5: Misura della lunghezza d'onda del fo-
l'elettrone si comporta come un'onda di lunghezza
tone diuso dopo scattering Compton in funzione
λ=
dell'angolo di osservazione.
dove
ne diusa, qualunque sia la direzione, ha la stessa frequenza (e quindi la stessa lunghezza d'onda se il mezzo di propagazione non cambia) della
radiazione incidente.
Per spiegare il fenomeno, Compton prese spunto dalle nuove teorie riguardanti l'interpretazio-
= h/2π
e
h
=⇒ p = k ,
p
k = 2π/λ
è il numero d'onda.
L'equazione precedente viene detta relazione di
de Broglie.
1.3.2 Esperienza di Davisson e Germer
ne quantistica della radiazione elettromagnetica, e
Nell'esperienza di Davisson e Germer (1927) un fa-
ipotizzò che la parte dell'energia persa dalla radia-
scio di elettroni era diretto verso un cristallo di nic-
1.4 Spettri di emissione degli atomi e modello di Bohr
5
kel, che poteva essere ruotato per misurare la distribuzione angolare degli elettroni. Si trovò che a certi
angoli si aveva un picco nell'intensità degli elettroni
diusi, in accordo con la condizione di interferenza
costruttiva tra onde elettroniche riesse da diversi
piani reticolari, in maniera identica a quello accade
con i raggi X.
I risultati erano in accordo quantitativo con la
relazione di de Broglie.
Ad esempio ad un elettrone che si muove a velov = 107 m/s è associata una lunghezza d'on−11
m, dell'ordine delle distanze
da λ 7 × 10
cità
interatomiche.
1.4
Figura
1.6:
Meccanismi
di
emissione
e
di
assorbimento della luce.
Spettri di emissione degli
atomi e modello di Bohr
Un altro grande problema irrisolto all'inizio del ventesimo secolo riguardava gli atomi.
Da un lato
il modello in base al quale gli elettroni (negativi)
orbitano attorno al nucleo comportava l'instabilità
dell'atomo: gli elettroni avrebbero dovuto perdere
Figura 1.7: Onde stazionarie di de Broglie per un
energia per l'irraggiamento che compete alle cariche
elettrone in un'orbita circolare.
accelerate, e quindi cadere nel nucleo. Inoltre, se la
radiazione da parte degli atomi è legata a cambiamenti di energia nel moto degli elettroni, lo spettro
di luce emesso dagli atomi dovrebbe essere continuo. Si osserva al contrario che lo spettro della luce emessa da atomi energetici (sodio e mercurio ad
esempio) non è in generale continuo, ma composto
le orbite degli elettroni in un atomo per le quali
le onde di materia sono stazionarie possano essere
le sole orbite stabili (Figura 1.7). Se
r
è il raggio
dell'orbita, si deve avere
2πr = nλ ; n = 1, 2...
da righe individuali, come ci si aspetterebbe se solo
livelli discreti di energia fossero concessi agli elet-
e dunque, utilizzando la relazione di de Broglie
troni, e la luce venisse emessa nella transizione tra
due livelli (Figura 1.6).
Considerazioni analoghe
valgono per le energie assorbite.
Alla ne del diciannovesimo secolo si osservò che
le lunghezze d'onda della luce emessa dall'idrogeno
soddisfacevano alla relazione
1
= RH
λ
1
1
− 2
2
n
m
2πr = n
h
=⇒ L = pr = n .
p
Il momento angolare
L e' quindi quantizzato.
cavere la quantizzazione dei valori concessi per il
,
(1.2)
raggio. Abbiamo
un'opportuna
1 e2
4π0 r2
Nel modello di Bohr gli elettroni orbitano intor-
=⇒ EK
con
n < m
numeri interi e
RH
costante.
no al nucleo, essendo ad esso legati dall'attrazione
elettrostatica.
Se il comportamento degli elettroni è quello di
un'onda, è plausibile che gli stati stabili siano caratterizzati da onde stazionarie.
Dal-
la quantizzazione del momento angolare si può ri-
Supponiamo che
Ep
=⇒ EK + Ep = E
EK
mv 2
=2
r
r
2
1 e
=
(1.3)
4π0 2r
1 e2
= −
4π0 r
1 e2
= −
(1.4)
4π0 2r
= F =
1.5 Conclusione
6
(si noti che per descrivere un sistema idrogenoide,
un sistema cioè nel quale ogni atomo ha
protoni e un elettrone, è suciente nella precedente
1 e2
1 Ze2
espressione sostituire 4π r 2 con 4π r 2 ).
0
0
Da
L = mvr = n
m 2
1 e2
v = EK =
2
4π0 2r
(1.5)
(1.6)
v = n/mr
si ricava, sostituendo l'espressione di
•
Z > 1
I soli stati concessi per l'elettrone siano quelli
con
•
L = n,
e che non irradino;
L'atomo emetta o assorba radiazione quando
un elettrone passa da uno stato stazionario all'altro, e che, detta
∆E
la dierenza di energia
tra i due stati, la frequenza dell'onda associata
al fotone emesso sia
1.5
f = ∆E/h.
Conclusione
nella seconda equazione,
r = 4π0
Verso la ne del secolo scorso evidenze sperimentali
n2 2
≡ rn .
me2
indicarono tra l'altro la
Si noti che, come deve essere per stati legati:
ticelle mediante punti materiali e della radiazione
•
L'energia totale è negativa.
•
La media temporale dell'energia cinetica è pari
mediante onde erano insucienti.
alla metà della media temporale dell'energia
potenziale in modulo (teorema del viriale).
Il più piccolo valore del raggio concesso si dice
raggio di Bohr
C'era bisogno di un nuovo concetto per rappresentare gli enti sici. Per rappresentare i fenomeni
d'interferenza osservati, le particelle dovevano essere rappresentate da funzioni d'onda in uno spazio
almeno bidimensionale (per rendere conto di ampiezza e fase).
a0 :
a0 = 4π0
quantizzazione di fenomeni
sici, e il fatto che le rappresentazioni delle par-
Il più piccolo ambiente per que-
sta rappresentazione sono le funzioni complesse del-
2
= 0.053 nm .
me2
(1.7)
le coordinate spaziali e del tempo; il concetto più
semplice sembra quello di
Poiché il raggio e l'energia sono in relazione
onde di probabilità.
tramite la (1.4), si ricava per la quantizzazione
Problemi
dell'energia:
En = −
1 e2
1 e2 1
13.6 eV
=−
=−
.
4π0 2rn
4π0 2a0 n2
n2
È immaginabile che un elettrone, nel passare da
uno stato di energia
Ei
a uno stato di energia
Ef < Ei ,
emetta un quanto di energia (fotone) di
frequenza
f
tale che
f = (Ei − Ef )/h
Si ha dunque
2
f=
1
e
Ei − Ef
=
h
4π0 2a0 h
da cui
f
1
= = RH
λ
c
con
(Figura 1.6).
1
1
− 2
n2f
ni
1
1
− 2
n2f
ni
2
RH =
e
1
.
4π0 2a0 hc
Otteniamo quindi la relazione (1.2).
Bohr era arrivato alle stesse conclusioni prima dell'enunciato della relazione di de Broglie,
postulando che:
1. Calcolare l'energia e il momento di un fotone rosso, con lunghezza d'onda
λ=650
nm e
calcolare la lunghezza d'onda di un fotone con
energia pari a 2.0 eV.
2. Sapendo
che
tungsteno è
il
potenziale
Vs = 4.52
d'estrazione
del
eV, determinare la fre-
quenza di soglia fotoelettrica per questo metallo, la massima energia cinetica dei fotoelettroni quando la radiazione ha lughezza d'onda
di 200 nm ed il potenziale di arresto in questo
caso.
3. Utilizzando la legge di Wien, calcolare la lunghezza d'onda alla quale un oggetto a tem◦
peratura ambiente (T=20 C) emette la massima radiazione termica e stabilire no a quale
temperatura va riscaldato l'oggetto perché si
presenti di colore rosso (λ=650 nm).
4. Raggi X di lunghezza d'onda 0.24 nm sono diffusi secondo la relazione di Compton e il fascio
1.5 Conclusione
diuso è osservato ad un angolo di
7
60◦
rispet-
to la direzione di incidenza. Calcolare la lunghezza d'onda dei raggi X diusi, l'energia dei
fotoni X diusi, l'energia degli elettroni diusi
e la loro direzione rispetto quella d'incidenza.
5. Stimare le lunghezze d'onda di de Broglie per
(a) un'automobile dal peso di 1000 kg che viaggia a 100 km/h e (b) un protone con energia
di 150 MeV.
Capitolo 2
Funzione d'onda ed equazione di
Schrödinger
Se i corpi luminosi sono carichi d'incertezza, non resta che adarsi al buio, alle regioni deserte del cielo. Che cosa può esserci
di piú stabile del nulla? Eppure anche del
nulla non si può essere sicuri al cento per
cento. Palomar dove vede una radura del rmamento, una breccia vuota e nera, vi ssa
lo sguardo come proiettandosi in essa; ed ecco
che anche lì prende forma un qualche granello
chiaro (...)
2.1
Le proprietà della funzione
d'onda
Vediamo a quali proprietà fondamentali devono
soddisfare le funzioni d'onda associate a una particella,
per essere adatte a interpretare i fatti
sperimentali.
Se vogliamo rendere conto dell'interferenza fra
particelle le funzioni d'onda devono essere a valori
complessi.
Italo Calvino
Palomar
Vogliamo che laddove il modulo dell'ampiezza
dell'onda è grande, più facile sia trovare la particella. Il modo più semplice è imporre la proporzionalità tra il modulo quadro dell'ampiezza dell'onda
w
e la probabilità
Intorno al 1926 Erwing Schrödinger formulò una
teoria fenomenologica che diede un contributo importantissimo allo sviluppo della sica quantisti-
di trovare la particella in quel
punto e a quell'istante:
dw(r, t) ∝ |Ψ(r, t)|2 dV = Ψ∗ (r, t)Ψ(r, t) dV
(2.1)
ca, scrivendo per le funzioni d'onda un'equazione
che esprime la probabilità di trovare la particel-
analoga alle equazioni della meccanica classica.
la nel volume
dV .
La relazione di proporzionali-
Esaminando risultati fenomenologici sulla funzio-
tà nell'equazione precedente diviene una relazio-
ne d'onda, in questo capitolo formuleremo le pri-
ne di uguaglianza se si impone la condizione di
me interpretazioni di fenomeni caratteristici della
normalizzazione:
sica quantistica, quali ad esempio il principio di
Heisenberg, l'eetto tunnel e l'esistenza di energie
V
cinetiche minime per gli stati di un sistema sico.
Cominceremo analizzando le proprietà essenziali
che deve possedere la funzione d'onda associata ad
una particella materiale,
Ψ(r, t),
e successivamen-
te le proprietà dell'equazione adatta a descrivere
normalizzando la
fattore.
dV |Ψ(r, t)|2 = 1
Ψ(r, t)
mediante un opportuno
L'integrale è esteso a tutto il volume
V
in cui la particella è osservabile.
Inoltre imporremo che le
Ψ(r, t)
siano funzio-
la propagazione di una tale funzione d'onda: l'e-
ni continue con derivate parziali prime continue
quazione che adotteremo in approssimazione non
in ogni punto dello spazio, esclusi al più punti di
relativistica è l'equazione di Schrödinger.
frontiera del dominio (di misura nulla).
2.2 L'equazione di Schrödinger
9
Per spiegare i risultati dell'interferenza delle onde
materiali e per motivi di semplicità è desiderabile
che per le funzioni d'onda valga il principio di sovrapposizione. Questa proprietà, che viene riscontrata normalmente in elettromagnetismo (si pensi
alla luce), può essere descritta aermando che se
Ψ1 (r, t)
due funzioni d'onda
e
Ψ2 (r, t)
sono valide
Per le note relazioni di Planck e de Broglie la (2.3)
diventa:
2 k 2
.
(2.4)
2m
Se ipotizziamo che la Ψ(x, t) come onda piana abbia
i(kx−ωt)
forma matematica Ψ(x, t) = e
, derivando
ω =
rispetto al tempo otteniamo:
descrizioni di una particella, lo è anche la loro combinazione lineare
c1 Ψ1 (r, t) + c2 Ψ2 (r, t)
con
c1
e
∂Ψ(x, t)
= −iωΨ(x, t)
∂t
c2
numeri complessi.
mentre
2.1.1 Flusso di probabilità
se
d'onda è analogo al usso di energia per un'onda
ordinaria.
Così come il usso di energia in un'onda attra-
A
vale
dE/Adt = (dE/dV )v⊥ ,
dove
due
volte
rispetto
alla
otteniamo:
(2.6)
Sostituendo nella (2.4) le espressioni di
ω
k2
e
che si ricavano dalle (2.5) e (2.6) otteniamo inne:
v⊥ è la componente della velocità normale all'area
A, il usso di probabilità per la funzione d'onda Ψ
vale
x
∂ 2 Ψ(x, t)
= i2 k 2 Ψ(x, t) .
∂x2
Il usso (corrente) di probabilità per la funzione
verso un'area
deriviamo
direzione del moto
(2.5)
i
2 ∂ 2 Ψ(x, t)
∂Ψ(x, t)
=−
,
∂t
2m ∂x2
(2.7)
che è proprio l'equazione di Schrödinger cui deve
2
dw/Adt = (dw/dV )v⊥ = |Ψ(r, t)| v⊥ .
(2.2)
soddisfare la funzione d'onda di particelle libere
non relativistiche. Essa corrisponde a quella che in
meccanica classica si direbbe l'equazione del moto
2.2
L'equazione di Schrödinger
a potenziale costante.
In
presenza di
un
potenziale
si
ottiene,
ag-
La teoria dell'equazione di Schrödinger riguarda
giungendo al termine cinetico nella (2.4) l'energia
un'equazione d'onda che deve descrivere le onde
potenziale
materiali associate a una particella secondo l'ipotesi
di Louis de Broglie.
La funzione d'onda è una funzione a valori complessi della posizione e del tempo. In base a quanto
detto precedentemente a proposito del principio di
sovrapposizione, l'equazione della quale essa è soluzione dovrà essere lineare; in particolare, se a una
denita funzione d'onda
Ψ(r, t)
corrisponde un de-
nito stato di moto della particella, anche la funzioiγ
ne e Ψ(r, t), dove γ è una costante reale arbitraria,
descriverà lo stesso stato: il signicato sico di entrambe sarà identico per la (2.1). Quindi, mentre a
ogni funzione d'onda corrisponde uno stato di moto
univoco della particella, l'inverso è vero a meno di
un fattore complesso di valore assoluto 1.
Nel seguito per semplicità ci restringeremo ad un
problema unidimensionale.
Consideriamo dappri-
m, in moto lungo
l'asse x con una quantità di moto p. La sua energia
ma una particella libera di massa
sarà
p2
.
E=
2m
(2.3)
i
U (x, t):
2 ∂ 2 Ψ(x, t)
∂Ψ(x, t)
=−
+ U (x, t)Ψ(x, t) .
∂t
2m ∂x2
(2.8)
Nel caso tridimensionale l'equazione precedente
diviene naturalmente:
i
dove
∂Ψ(r, t)
2 2
=−
∇ Ψ(r, t) + U (r, t)Ψ(r, t) ,
∂t
2m
∇2
(2.9)
è il laplaciano.
2.2.1 Nota sugli operatori
Osserviamo che nell'equazione di Schrödinger tutto
funziona come se si fosse sostituito alla componente
della quantità di moto lungo l'asse
p̂x = −i
x
l'operatore
∂
,
∂x
che agisce sulla funzione d'onda, e quindi
pˆ = −i∇ .
(2.10)
2.3 L'equazione di Schrödinger stazionaria
Questo è vero in generale (come vedremo in un
10
Calcolando la derivata seconda spaziale e la
capitolo successivo): in meccanica quantistica al-
prima temporale avremo:
le osservabili sono associati opportuni operatori
2 ∂ 2 ψ(x)
∂ϕ(t)
= ϕ(t) −
iψ(x)
+ U (x)ψ(x) .
∂t
2m ∂x2
(cioè enti matematici che portano una funzione in
un'altra).
Si noti il cappellino
(hat) ad indicare l'operatore.
Dividendo inne ambo i membri per
ψ(x)φ(t)
L'operatore momento angolare
In analogia con la meccanica classica, deniamo
l'operatore momento angolare dalla
ˆ
L = rˆ × pˆ = −ir × ∇ .
I due membri dell'uguaglianza dipendono rispet-
In coordinate polari il quadrato dell'operatore
L̂ = −
2
1 ∂
sin θ ∂θ
∂
1 ∂2
.
sin θ
+
∂θ
sin2 θ ∂φ2
L'equazione
di
li. Essendo uguali, essi devono essere uguali a una
costante; chiamiamola
(2.11)
2.3
2
i ∂ϕ(t)
∂ 2 ψ(x)
=−
+ U (x) .
ϕ(t) ∂t
2mψ(x) ∂x2
tivamente solo dalle coordinate temporali e spazia-
momento angolare si esprime come
2
Schrödin-
ger stazionaria
rivate parziali; in casi particolari essa può esse-
−
−
variabili.
Per il momento limitiamoci per semplicità al caso
unidimensionale. Supponiamo che il potenziale sia
U (x, t) = U (x);
φ
dipende solo da
la (2.8)
2 ∂ 2 Ψ(x, t)
∂Ψ(x, t)
=−
i
+ U (x)Ψ(x, t) .
∂t
2m ∂x2
(2.12)
Ψ(x, t) si
ϕ(t) dipenden-
Proviamo una soluzione nella quale la
possa scrivere come prodotto di una
posizione
=
Eψ(x)
=
Eϕ(t) ,
e la
ψ
solo da
x,
Risolviamo
la
solo dalla variabile
x,
semplice
=
Eψ(x) (2.13)
=
Eϕ(t) . (2.14)
(2.14)
separando
le
variabili. Otteniamo:
ϕ(t) = e−i
poiché,
Et
;
per la relazione di Einstein-Planck,
eguaglia l'energia della particella,
E
ω
si identica
con l'energia totale.
La soluzione dell'equazione di Schrödinger per un
potenziale indipendente dal tempo è dunque una
funzione del tipo
Ψ(x, t) = ψ(x)ϕ(t) .
Sostituendo nella (2.12) otterremo:
∂(ψ(x)ϕ(t))
=
i
∂t
−
t
2 d2 ψ(x)
+ U (x)ψ(x)
2m dx2
dϕ(t)
i
dt
diviene:
ψ(x)
Si hanno quindi le due
2 ∂ 2 ψ(x)
+ U (x)ψ(x)
2m ∂x2
∂ϕ(t)
i
∂t
che, poiché la
re risolta attraverso la tecnica di separazione delle
te solo dal tempo ed una
E.
equazioni dierenziali ordinarie:
possono essere scritte:
L'equazione di Schrödinger è un'equazione alle de-
indipendente dal tempo,
Ψ(x, t) =
separiamo le variabili:
2 ∂ 2 (ψ(x)ϕ(t))
+ U (x)(ψ(x)ϕ(t)) .
2m
∂x2
Ψ(x, t) = ψ(x)e−i
dove la
ψ(x)
Et
viene dalla soluzione della (2.13), che
è detta equazione di Schrödinger stazionaria.
Si
noti che la (2.13) è un'equazione agli autovalori; le funzioni che la risolvono vengono chiamate
autofunzioni (eigenfunctions).
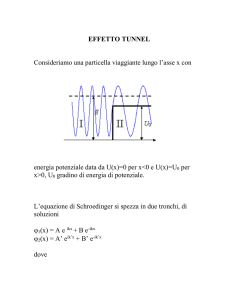
2.4 Buca di potenziale
11
2.3.1 Particella libera
Il caso più semplice di moto in una dimensione si
ha per un valore di potenziale costante (particella
libera); senza ledere la generalità possiamo porre
U (x) = 0.
L'equazione stazionaria diventa:
−
Le
2 d2 ψ(x)
= Eψ(x) .
2m dx2
autofunzioni
Ψ(x, t) sono legate
ψ(x)e−iEt/ .
ψ(x)
e
le
funzioni
dalla nota relazione
d'onda
Ψ(x, t) =
Sappiamo che gli autovalori sono uguali all'energia totale
E
della particella; per quanto detto pre-
cedentemente sono accettabili le soluzioni tali che
E ≥ 0.
È nota anche la struttura matematica di
una possibile funzione d'onda soluzione di questo
Figura 2.1: Buca di potenziale.
problema, l'onda piana:
Ψ(x, t) = ei(kx−ωt) .
Qui nel seguito studieremo il caso limite in cui
Se risolviamo l'equazione stazionaria otteniamo
ψ(x) = Aeikx + Be−ikx (k =
√
2mE/)
la barriera ha pareti d'altezza innita, e quindi la
particella è connata nella regione
U (x) =
e dunque
con
Ψ(x, t) = Aei(kx−ωt) + Be−i(kx+ωt)
√
k = 2mE/.
−2 d2 ψ
= Eψ ,
2m dx2
La soluzione più generale è dunque la combinaa una particella che viaggia nel verso positivo del-
x
x,
entrambe delocalizzate (la probabilità
e di una che viaggia nel verso negativo delle
|Ψ∗ Ψ| di
trovarle in un punto qualunque non dipende da
0 0 ≤ x ≤ a;
∞ altrimenti.
Cerchiamo stati stazionari, cioè soluzioni della
zione lineare di una funzione d'onda corrispondente
le
0 < x < a:
x).
con
ψ(0) = ψ(a) = 0 poiché ψ = 0 dove U
Si ottiene
d2 ψ
= −k 2 ψ con k =
dx2
è innita.
√
2mE
,
le cui soluzioni sono del tipo
2.4
ψ(x) = Aeikx + Be−ikx .
L'equazione di Schrödinger
e la buca di potenziale
Conviene ora usare la rappresentazione attraverso funzioni trigonometriche:
La congurazione del potenziale in questo caso
è descritta nella Figura 2.1.
seguente:


U0
U (x) = 0


U0
La situazione è la
Risulta evidente che per avere
x < 0;
0 ≤ x ≤ a;
x>a
Tale situazione viene detta buca di potenziale di
pareti nite, e una particella materiale viene connata nella regione
costanti niti
U0
ψ(x) = (A + B) cos(kx) + i(A − B) sin(kx) .
0 < x < +a
del potenziale.
fra due valori
ψ(0) = 0
il primo
addendo deve essere nullo; quindi
ψ(x) = Ã sin(kx) .
Se vogliamo che il modulo quadro della funzione,
a, dia 1, dovremo avere à =
che ψ(a) = 0 avremo
nπx
2
sin
ψn (x) =
a
a
integrato fra 0 e
Imponendo
2/a.
(2.15)
2.4 Buca di potenziale
12
Figura 2.3:
Energia potenziale per una molecola
biatomica, e spettro degli autovalori.
Figura 2.2: Autofunzioni concesse per la buca di
potenziale innita e livelli di energia.
2.4.2 Estensione al caso bidimensionale
E' un'importante estensione del caso precedente.
con
2 n2 π 2
En =
= n2
2m a2
e
n
intero
2 π 2
2ma2
Ora la particella è vincolata da una barriera di ener-
gia innita a rimanere in un piano
2
≡ n E0
positivo (per n = 0 l'autofunzione non è
normalizzabile).
Le energie concesse sono dunque quantizzate come i livelli energetici degli elettroni nell'atomo di
idrogeno (l'energia è proporzionale al quadrato di
un numero quantico
n).
to di minima energia (n
Si nota inoltre che lo sta-
= 1)
ha energia cinetica
maggiore di 0.
2.2 e corrispondono agli stati stazionari.
2 d2 ψ
+ U (x)ψ = Eψ ,
2m dx2
per
x → ±∞.
Se
E > U0 ,
E < U0 ,
valida per gli
nel caso in una dimensione, anche se ora si tratta di
estendere lo schema ad un problema a due variabili:
2 ∂ 2 ψ(x, y)
−2 ∂ 2 ψ(x, y)
−
+ U (x, y)ψ(x, y)
2m
∂x2
2m ∂y 2
= Eψ(x, y) .
La soluzione di quest'equazione richiede opporIl
buon senso ci suggerisce comunque di ammettere che la densità di probabilità fuori dalla bu-
ta,
All'interno si usa co-
ψ(x, y) = X(x)Y (y),
dove
X
e
Y
risultano
funzioni esattamente del tipo ottenuto nel caso
X(x)
entrambe le
tutti gli stati energetici sono concessi (spettro conSe
ne di Schrödinger segue la stessa strategia delineata
unidimensionale:
soluzioni sono oscillanti e non ci sono stati legati;
tinuo).
(ad esempio
me soluzione di prova una funzione fattorizza-
L'equazione di Schrödinger stazionaria è
U → U0
xy
La soluzione dell'equazio-
ca sia identicamente nulla.
2.4.1 Nota sugli stati legati
con
a).
tune tecniche di separazione delle variabili.
Le autofunzioni stabili sono illustrate in Figura
−
un quadrato di lato
c'è una soluzione sicamente
autovalori dell'energia E .
La gura 2.3 rappresenta un esempio: il poten-
= Ax sin kx x + Bx cos kx x
Y (y) = Ay sin ky y + By cos ky y ,
e i numeri d'onda
kx , ky
sono ora richiesti sepa-
ratamente soddisfare alle condizioni di stazionarietà perché la soluzione di prova sia accettabile. Applicando le condizioni di continuità ai bordi,
ziale di interazione di una molecola biatomica in
ψ(0, y) = ψ(x, 0) = ψ(a, y) = ψ(x, a) = 0
funzione della distanza (per una soluzione appros-
ancora una situazione di stazionarietà di onde in
simata nell'intorno della posizione di equilibrio si
due dimensioni (analogamente al caso della vibra-
veda il capitolo 4).
zione di una membrana piana vincolata ai bordi,
si ottiene
2.5 Il principio d'indeterminazione (di Heisenberg)
come la pelle di un tamburo).
k
za i numeri d'onda
In corrisponden-
13
quantità di moto lungo
risultano quantizzati, e l'e-
∆px ∆x .
nergia è ancora quantizzata ed assegnabile in funzione di due numeri quantici. La funzione d'onda
normalizzata che si ottiene è
ψ(x, y) =
La relazione sopra enunciata viene chiamata
principio d'indeterminazione posizione-momento.
2
sin(nx πx/a) sin(ny πy/a)
a
Anche tra energia e tempo in cui quest'energia
viene misurata esiste un'analoga relazione d'indeterminazione.
e l'energia
una funzione
2 2
E = E(nx , ny ) =
π
(n2 + n2y ) = E0 (n2x + n2y ) .
2ma2 x
Infatti un'onda è esprimibile come
f (kx − ωt):
no per la coppia
(E = ω, t).
(p = k, x)
ci dierenti (dunque dierenti funzioni d'onda) che
danno la stessa energia. I valori
danno entrambi
particolare
Il caso appena citato è tutto sommato accettabile
in quanto le due coppie di numeri quantici corrispondono ad uno scambio degli assi coordinati. In
realtà la situazione può essere più complessa:
(nx , ny ) = (1, 7)
spondono alla stessa
le
(nx , ny ) = (5, 5) corrienergia, 50E0 . Ma le funzioni
e
d'onda (e i loro moduli quadrati) sono di natura sostanzialmente dierente. La degenerazione è tipica
di sistemi a più dimensioni (in realtà esistono aascinanti connessioni fra la simmetria di un sistema
sico e le possibili degenerazioni quantistiche).
Quanto detto si estende banalmente al caso di
una buca di potenziale tridimensionale.
(2.17)
L'energia non è quindi misurabile al meglio di
∼ /∆t,
e questo è anche il limite intrinseco alla
conservazione dell'energia. Su una scala di tempo
(nx , ny ) = (2, 1) e
E = 5E0 . Questo ∆t,
è un primo esempio di degenerazione quantistica.
valgo-
Si avrà dunque in
∆t∆E .
Osserviamo che vi sono coppie di numeri quanti-
coppie
tutte le considerazioni
fatte per la coppia di variabili
Degenerazione
(nx , ny ) = (1, 2)
x
si possono produrre quanti di energia
no a
/∆t.
virtuali
2.5.1 Interpretazione del principio
d'indeterminazione
In un'onda piana la lunghezza d'onda (o il numero d'onda,
k)
sono perfettamente deniti, e l'onda
è totalmente delocalizzata nello spazio.
Essa non
sembra dunque adatta a descrivere una particella
nel senso di de Broglie.
A prescindere da questo
aspetto, è peraltro chiaro che sovrapponendo due
onde piane di diversa lunghezza d'onda si assiste
ad un fenomeno più o meno marcato di battimento:
l'onda risultante tende periodicamente a localizzarsi in corrispondenza delle interferenze costruttive.
Aggiungendo altre lunghezze d'onda la sovrapposi-
2.5
Il principio d'indetermina-
sumere l'aspetto di un pacchetto localizzato in una
zione (di Heisenberg)
zona di ampiezza
Abbiamo visto che a dierenza del caso classico,
una particella connata in un segmento di lunghezza
a = 2∆x
non può stare ferma. La sua quantità
di moto è incerta (non è noto il verso), e la minima
incertezza possibile eguaglia in ordine di grandezza il modulo della quantità di moto corrispondente
alla minima energia
E1 ,
e cioè
π
π
=
∼
∆px = |px | = 2mE1 =
a
2∆x
∆x
Chiamando
dinata
x
e
zione tende sempre più a concentrarsi, no ad as-
∆x.
La posizione viene determi-
nata sempre meglio a spese della lunghezza d'onda,
in modo che
∆x∆k ∼ 1:
se l'onda è poco sparpa-
gliata, è dicile ottenere una stima precisa della
sua lunghezza d'onda e viceversa. Lo stesso discorso è fattibile nel dominio del tempo: per un'onda
viaggiante, la determinazione precisa della frequenza temporale richiede un tempo lungo di ripetizioni cicliche ovvero, se l'onda dura poco tempo, la
sua frequenza sarà male determinata:
∆t∆ω ∼ 1.
E' ora possibile estendere queste regole di indeter-
(2.16)
minazione all'onda di de Broglie con fondamentali
∆x l'incertezza sul valore della coor-
conseguenze nella comprensione sica del modello
∆px
l'incertezza sulla componente della
ondulatorio della materia.
2.6 Altri potenziali 1-dimensionali costanti a tratti
14
p = k , dalla ∆x∆k ∼ 1 si
∆x∆px ∼ . Analogamente, dalla E = ω
∆t∆ω ∼ 1 si ottiene ∆t∆E ∼ . Queste
Tenuto conto che
ottiene
e dalla
due relazioni costituiscono la forma (rispettivamente spazio-momento ed energia-tempo) del principio
di indeterminazione di Heisenberg. In pratica esso
stabilisce l'impossibilità di determinare simultaneamente con precisione assoluta posizione e velocità
(energia e tempo) di una particella. Le implicazioni sono profonde: è facile accettare e comprendere l'indeterminazione spaziale di un'onda del mare
(viste le argomentazioni classiche sulle onde piane
sopra descritte), ma per una particella materiale
questo è molto più complicato e comunque al di
fuori della portata del senso comune. Di fatto è la
natura stessa che impone un limite all'accuratezza
Figura 2.4: Gradino di potenziale.
con la quale possiamo eettuare misure. Considerando ad esempio un elettrone con velocità lungo x
6
pari a 3.6 10 m/s, nota con precisione dell'1%, la
precisione nella posizione lungo x stimata a partire
−24
−26
da: px = 3.3 · 10
kg m/s e ∆px = 3.3 · 10
kg
−9
m/s, è ∆x /∆px =0.5·10
m (dell'ordine del
elettrico dell'onda, la probabilità quantistica è proporzionale al modulo quadro dell'ampiezza d'onda
di de Broglie.
diametro atomico).
Insomma la rappresentazione ondulatoria implica che, per descrivere una particella localizzata nello spazio, abbiamo bisogno della combinazione li-
2.6
Soluzione per altri potenziali
unidimensionali
co-
k. Il nuk corrisponde, attraverso la relazione
Broglie p = k , alla quantità di moto: quin-
Cominciamo a passare i rassegna le soluzioni dell'e-
di la quantità di moto di una particella localizzata
quazione di Schrödinger stazionaria in una dimen-
neare di onde con diversi numeri d'onda
stanti a tratti
mero d'onda
di de
nello spazio non potrà essere ben denita.
Se si prepara un sistema sico in un certo modo, potremo misurare grandezze rilevanti entro la
loro indeterminazione. Ripetendo la misura si otterranno valori dierenti, anche se lo stato iniziale
del sistema è lo stesso. Si evidenziano dunque forti
sione per altri tipi di potenziale
U (x).
Accennere-
mo anche alle conferme sperimentali delle previsioni
teoriche ottenute.
2.6.1 Gradino di potenziale
connessioni con la teoria della probabilità e statisti-
Nella Figura 2.4 viene schematizzato il problema
ca: è impossibile prevedere il singolo evento, ma con
di una particella libera che procedendo secondo le
tante misure (o con tanti sistemi eguali) si giunge
ad una distribuzione di probabilità. La meccanica
x crescenti incontra un potenziale costante U (x) =
U0 . Questa congurazione viene detta del gradino
quantistica fornisce l'apparato matematico per cal-
di potenziale.
colare tali distribuzioni. C'è una dierenza critica
Il potenziale è così denito:
fra statistica e meccanica quantistica: nella prima
l'indeterminismo è causato dalla incompleta conoscenza del sistema all'inizio, nella seconda l'inde-
U (x) =
0
U0
x<0
altrove .
terminismo è intrinseco alla natura, insuperabile.
L'ampiezza dell'onda di de Broglie è collegata al-
Fisicamente questa situazione approssima il po-
la probabilità di trovare la particella: così come la
tenziale per un elettrone in un metallo in prossimità
probabilità di trovare il fotone di Planck è propor-
della supercie. All'interno del metallo l'elettrone
zionale al modulo quadro dell'ampiezza del campo
è sottoposto all'azione di un potenziale costante,
2.6 Altri potenziali 1-dimensionali costanti a tratti
mentre fuori dalla supercie incontra un potenziale
15
Si ha dunque
bruscamente superiore.
Distinguiamo due casi:
a. la particella proveniente dalle
energia cinetica
x
negative ha
E < U0 .
Classicamente la situazione viene descritta me-
D
2 (1
D
2 (1
=
=
+ i kk21 )
− i kk21 )
Le funzioni d'onda corrispondenti sono

k2 ik1 x −iωt
D

e
 2 (1 + i k1 )e
k2 −ik1 x −iωt
D
+ 2 (1 − i k )e
e

 −k2 x −iωt1
De
e
diante una forza di tipo impulsivo che per un
tempo brevissimo agisce sulla particella nella
posizione
A
B
x = 0, nel verso delle x decrescenti, e
che determina per il teorema dell'impulso una
x<0
x≥0
variazione nita del momento della particella.
La particella non può penetrare nella regione
delle
x
positive poiché la sua energia cinetica
L'interpretazione sica della prima è che per
la regione delle
x<0
la sovrapposizione delle
diverrebbe negativa. Quindi secondo la mecca-
funzioni d'onda forma un'onda stazionaria con
nica classica la particella deve invertire il verso
un'onda incidente ed una riessa. Calcoliamo
R che classicamente
del suo moto e rimbalzare sul gradino di po-
il coeciente di riessione
tenziale con un momento uguale in modulo ed
è dato dal rapporto fra le ampiezze dell'onda
opposto in verso a quello di incidenza , con2
servando l'energia cinetica E = p /2m. Nel
riessa
punto d'inversione
x=0
e
p = 0.
B
e quella
A
dell'onda incidente.
Data l'espressione del usso (corrente) di pro-
Nel caso quantistico scriviamo l'equazione di
babilità ricavata nella (2.2), avremo R =
vrif B ∗ B/(vinc A∗ A (in questo caso le veloci-
Schrödinger stazionaria per le due regioni:
tà delle onde riessa e incidente sono uguali).
Si ottiene:
2 d2 ψ(x)
−
2m dx2
2 d2 ψ(x)
−
+ U0 ψ(x)
2m dx2
= Eψ(x) (x < 0)
= Eψ(x) (x ≥ 0) .
zioni raccordando le soluzioni per
x=0
dove
le autofunzioni dovranno essere univoche, continue e nite, assieme alle derivate prime. Si
arriva alle soluzioni:
 ik1 x
1x
Ae
+ Be−ik


√
 

 k1 = 2mE
k2 x
(1 − ik2 /k1 )∗ (1 − ik2 /k1 )
B∗B
=
= 1.
∗
A A
(1 + ik2 /k1 )∗ (1 + ik2 /k1 )
Il valore 1 esprime il risultato che la particella
Si risolvono separatamente queste due equa-
ψ(x) =
R=
x<0
viene sempre riessa per
Ce
+ De

x≥0

√


2m(U0 −E)

 k2 =
in accordo
ne quantistica sorprendente è che la probabilità di trovare la particella oltre il gradino non
è zero. Infatti nella regione
x > 0:
Ψ∗ Ψ = D∗ D × ψ ∗ ψ × ϕ∗ ϕ = |D2 |e−2k2 x
con
−k2 x
E < U0 ,
con la meccanica classica. Tuttavia la previsio-
k2
reale.
La probabilità di trovare la particella a
x>0è
nita e nonnulla. Questo fenomeno quantistico
viene detto penetrazione nella regione proibita
classicamente.
C=0
si ottiene dalla necessità di normalizza-
bilità; la condizione di continuità fra le autofunzioni e tra le loro derivate nel punto
implica:
D
−k2 D
= A+B
= ik1 A − ik1 B
x=0
b. la particella proveniente dalle
energia cinetica
x
negative ha
E > U0 .
Classicamente la particella procede con una
energia totale E e momento p1 tale che E =
p21 /2m nella regione delle x < 0 nel verso positivo dell'asse. Nel punto x = 0 è sottoposta ad una forza che la rallenta nel suo moto;
2.6 Altri potenziali 1-dimensionali costanti a tratti
p2
nella seconda regione ha momento
(E − U0 ) = p22 /2m.
16
tale che
Si avrà


Aeik1 x + Be−ik1 x
ψ(x) =
√
x < 0 k1 = 2mE
√
2m(E−U0 )
x ≥ 0 k2 =

Ceik2 x + De−ik2 x
Ricordiamo che classicamente una particella in
questa situazione sica ha probabilità 1 di attraversare il gradino nel punto
x = 0.
Vediamo
che cosa accade quantisticamente calcolando
come precedentemente le autofunzioni a meno
di una ampiezza e poi il coeciente di riessione e trasmissione. Se supponiamo dalle condizoni iniziali che non ci sia onda proveniente da
x → +∞,
avremo
raccordo in
x = 0:
C
k2 C
D = 0;
dalle condizioni di
Figura
B
C
Barriera


0
U (x) = U0


0
2
= A kk11 −k
+k2
1
= A k12k
+k2 .
k2 =
2 −ik1 x
Aeik1 x + A kk11 −k
+k2 e
2k1
ik2 x
A k1 +k2 e
Il primo addendo della
ψ(x)
per
con
una
x < 0;
0 ≤ x ≤ a;
x>a
Le autofunzioni sono quindi
ψ(x) =
potenziale,
Nella barriera di potenziale (Figura 2.5):
Supponiamo
di
2.6.2 La barriera di potenziale e
l'eetto tunnel
=A+B
= k1 (A − B)
Si ha dunque
2.5:
visualizzazione dell'eetto tunnel.
e poniamo
rappre-
k1 =
2mE
2 e
2m(U0 −E)
. Si ha
2

ik1 x

+ Ae−ik1 x
e
ψ(x) = Be−k2 x + Cek2 x

 ik1 x
De
x<0
x≥0
x<0
E < U0
x < 0;
0 ≤ x ≤ a;
x > a,
senta l'onda incidente mentre il secondo l'on-
dove il fattore moltiplicativo del primo termine
da riessa; la seconda equazione invece rap-
(onda incidente contro la barriera) è stato ssato
presenta l'onda trasmessa.
Calcoliamo ora
R = vB ∗ B/vA∗ A, cioè il coeciente di ries-
arbitrariamente all'unità.
sione quantistico, che rappresenta la probabili-
vo
tà della particella di essere riessa nella regione
vo non deve necessariamente annullarsi: l'integrale
x < 0:
della funzione non diverge essendo il dominio della
R=
k1 − k2
k1 + k2
2
A dierenza del risultato classico,
T = 1 − R.
C
dell'esponenziale con esponente reale e positi-
funzione stessa di misura nita.
Imponendo le condizioni di continuità abbiamo
0 < R < 1:
parte dell'onda viene riessa. Il coeciente di
trasmissione è
Si noti che in questo caso il fattore moltiplicati-
D=
−4ik1 k2
(k2 − ik1 )2 e(ik1 +k2 )a − (k2 + ik1 )2 e(ik1 −k2 )a
e la probabilità di passare dall'altra parte della
2.7 L'oscillatore armonico in una dimensione
(eetto tunnel) è proporzionale a
barriera
La soluzione di questa equazione porta a determinare un insieme di possibili valori di
4k12 k22
|D| = 2
,
2
2
(k1 + k2 ) sinh2 k2 a + 4k12 k22
2
che varia come un esponenziale decrescente in
ma è diversa da zero (per casa:
dell'energia
E.
γ
e cioè
L'equazione dierenziale è lineare
omogenea ma a coecienti non costanti. Per il me-
k2 a,
se ne calcoli il
valore).
2.7
17
todo di soluzione si rimanda alla bibliograa (p. es.
al testo di Greiner).
Alla ne dei calcoli si determina l'espressione
degli autovalori:
L'oscillatore
armonico
En = hf (n + 1/2) con n ∈ N0 .
in
una dimensione
Il valore di
E
dierisce da quello della teoria de-
classici sia quantistici è basata su forze di natura
gli oscillatori
E0 = 12 hf =
poiché ci dice
elastica, per la quale il moto è di tipo oscillato-
minima la particella sottoposta al potenziale (l'o-
rio armonico (per piccole oscillazioni). L'utilità di
scillatore) non può essere ferma, avendo comunque
Una situazione molto comune nei modelli sici sia
di Planck per una costante additiva
1
2 ω . Questo risultato è importante
che nello stato quantistico di energia
proporre la soluzione quantistica per questo caso
un'energia di punto zero
è che esso costituisce un valido punto di parten-
un'energia di punto zero è legata al principio di Hei-
za per la modellizzazione di sistemi sici di inte-
senberg: valgono considerazioni analoghe a quelle
resse reale (per piccoli spostamenti dall'equilibrio
fatte a proposito della buca di potenziale innita.
ogni energia potenziale ha andamento quadratico,
U (x) = kx2 /2).
seguente:
Un sistema conservativo a
N >1
gradi di liber-
te una trasformazione unitaria delle coordinate e
N
dove
sistemi unidimensionali.
L'impostazione classica di questo problema è la
seguente. Ponendo lo zero delle coordinate nel punto di equilibrio, la forza può essere descritta al
La presenza di
L'espressione delle autofunzioni normalizzate è la
tà può in generale venire diagonalizzato medianscomposto in
E0 > 0.
ψn (ξ) = An e−ξ
√
ξ = x β , le Hn sono
2
/2
i
Hn (ξ) ,
polinomi di Hermite
deniti dalla
Hn (ξ) = (−1)n eξ
prim'ordine dalla legge di Hooke
2
dn −ξ2
e
dξ n
e il fattore di normalizzazione vale
F = −kx
1
2
con k > 0 (U (x) U (0) + kx ); si ha dunque per
2
la seconda legge di Newton
d2
x + ω2x = 0
dt2
ω = 2πf = k/m ⇒ k = 4π 2 f 2 m
An =
√
β
√ n .
π2 n!
H0 (ξ)
H1 (ξ)
=
=
1
2ξ
Scriviamo ora l'equazione di Schrödinger stazio-
H2 (ξ)
H3 (ξ)
=
=
4ξ 2 − 2
8ξ 3 − 12ξ .
e dove
m
la massa della particella.
ψ(x)
U (0) = 0:
naria chiamando
ponendo
l'autofunzione incognita e
4π 2 f 2 m2 2
2m
d2
ψ(x)
−
x ψ(x) = − 2 Eψ(x)
dx2
2
e dunque, ponendo
2
γ = 2mE/2
e
(2.19)
I primi 4 polinomi di Hermite sono:
è
con
(2.18)
β = 2πmf /,
d
ψ(x) + (γ − β 2 x2 )ψ(x) = 0 .
dx2
Nella gura 2.6 sono riportati i graci delle prime
autofunzioni dell'oscillatore armonico: la densità di
probabilità (in funzione della coordinata
x)
per
n
basso è molto diversa rispetto all'occupazione nel
caso classico.
La corrispondenza migliora per alti valori di
n
(si veda la gura 2.7, dove l'andamento classico e
2.7 L'oscillatore armonico in una dimensione
18
2.7.1 Operatori di creazione e distruzione
Abbiamo visto che le autofunzioni normalizzate
per l'oscillatore armonico unidimensionale sono del
tipo:
ψn (ξ) = An e−(ξ
2
/2)
Hn (ξ)
Per polinomi di Hermite si ricavano le relazioni:
ξHn (ξ)
=
1
nHn−1 (ξ) + Hn+1 (ξ) (2.20)
2
d
Hn (ξ)
dξ
=
2nHn−1 (ξ) .
(2.21)
Si ricava dalle (2.19), (2.21) e (2.20) che
ξψn =
Figura 2.6: Prime autofunzioni dell'oscillatore ar-
x
monico in funzione dello spostamento
dalla po-
sizione di equilibrio: sopra l'autofunzione, sotto la
densità di probabilità.
n/2ψn−1 + (n + 1)/2ψn+1
d
ψn = 2 n/2ψn−1 − ξψn
dξ
(2.22)
(2.23)
da cui, inserendo la (2.22) nella (2.23)
d
ψn = n/2ψn−1 − (n + 1)/2ψn+1 ,
dξ
(2.24)
che sommata e sottratta alla (2.22) dà:
1
√
ξ+
2
1
√
ξ−
2
Deniamo
d
ψn
dξ
d
ψn
dξ
i
primi
operatore di distruzione
â
=
â+
classica (linea tratteggiata) per
n=1
e
=
√
nψn−1
(2.25)
=
√
n + 1ψn+1 .
(2.26)
membri
â
n=6.
rispettivamente
â+ :
e di creazione
1
√
ξ+
2
1
√
ξ−
2
Figura 2.7: Probabilità quantistica (linea continua)
e inverso della velocità per la soluzione in meccanica
=
d
dξ
d
.
dξ
(2.27)
(2.28)
Essi operano nel modo seguente:
âψn
+
â ψn
quello quantistico sono confrontati per diversi valori di
n).
=
=
√
nψn−1
√
n + 1ψn+1 .
(2.29)
(2.30)
L'andamento classico è rappresentato
dall'inverso del modulo della velocità, che è pro-
Vediamo come agiscono su un generico stato di
n:
porzionale alla probabilità di trovare il corpo in un
numero quantico
punto a un istante di tempo arbitrario.
sforma l'autofunzione dello stato
l'operatore di creazione tra-
stato immediatamente superiore
Si noti inne che poiché il potenziale è simmetrico le autofunzioni sono pari o dispari rispetto a un
cambiamento di segno della
x.
n in quella dello
n + 1, viceversa
l'operatore di distruzione trasforma l'autofunzione
dello stato
n
in quella dello stato immediatamente
precedente di numero quantico
n − 1.
2.7 L'oscillatore armonico in una dimensione
19
Si osservi che l'energia è quantizzata ed assegnata
in termini di un unico numero quantico
n
secondo
la semplice relazione
E = E(n) = (n + 1/2)ω
dove ω = k/m ; n = 0, 1, 2, ... .
La sequenza di livelli energetici (lo spettro del sistema) è ora equispaziata (cosa che non accade per la
Figura 2.8:
Schema della transizione tra livelli
particella in una scatola di energia innita). Anche
qui il livello energetico più basso è maggiore di 0,
mediante assorbimento/emissione di fononi.
a dierenza del caso classico. Questo è consistente
con il principio di Heisenberg.
Si ha
1
ψn = √ (â+ )n ψ0 .
n!
Si ha anche
Problemi
â+ âψn = nψn
1. Una palla da biliardo di massa m=100 g è posta su un piano entro la lunghezza di 1 m.
per cui possiamo denire l'operatore
Per il principio di indeterminazione dobbiamo
ammettere che la biglia abbia una piccola ve-
N̂ = â+ â
locità.
che ha gli stessi autovettori dell'hamiltoniamo e gli
autovalori
n.
Calcolarne il valore e commentare il
risultato.
L'operatore hamiltoniano può essere
2. Un elettrone è vincolato in una regione unidi-
espresso in termini degli operatori di creazione e
mensionale di lunghezza dell'ordine di un dia−10
metro atomico, 10
m. Quanta energia (mi-
distruzione mediante la:
Ĥ = hf
1
N̂ +
2
surata in eV) va fornita all'elettrone per pro-
.
(2.31)
l'energia più bassa? In questo stato di energia
Se inne applichiamo allo stato fondamentale
corrispondente
al
numero
muoverlo al primo stato eccitato a partire dal-
quantico
n = 0
â otteniamo:
d
ξ+
ψ0 = 0 .
dξ
l'operatore di distruzione
L'energia dell'oscillatore armonico nello stato ge-
minima, qual è la probabilità di trovare l'elet−10
trone nella regione fra 0.05 ×10
m e 0.15
−10
×10
m?
3. Calcolare l'intensità di riessione per una particella che incide contro un gradino di potenziale di altezza
a
E = eU0 ,
con
U0 con energia
e > 1. Qual è
cinetica pari
l'intensità di
riessione nel caso classico?
n è En = hf (n+1/2), dove per n = 0 si ottieE0 = hf /2.
Quindi lo stato generico ψn possiede l'energia En
più grande di quella minima di nhf . Ogni livello
4. Qual è il signicato sico della condizione di
energetico dierisce da quelli adiacenti di un quanto
5. Dimostrare che il valore atteso per
nerico
ne l'energia dello stato fondamentale:
hf ;
questo quanto per l'oscillatore armonico viene
detto
fonone.
Allora si può interpretare l'azione
+
degli operatori â , â sul generico stato ψn come
creazione o distruzione di un fonone.
Questi operatori giocano un ruolo fondamentale nella seconda quantizzazione dell'elettrodinamica
quantistica (QED), nella quale i quanti dei campi
d'onda dell'oscillatore sono i fotoni.
normalizzazione della funzione d'onda?
buca di energia innita
dimensione è dato da
x2 in una
e larghezza a in una
a2 [1/3 − 1/(2n2 π 2 )].
Qual è la dierenza più importante fra questo
risultato ed il valore atteso per
x?
Capitolo 3
Atomi
Non c`è alcuna possibilità che gli uomini un giorno accedano all'energia atomica.
Robert Millikan
Premio Nobel per la Fisica 1923
3.1
Potenziali a simmetria sferica
In problemi a simmetria sferica il potenziale
U (r)
dipende solo dalla distanza dall'origine, dove è posta
la sorgente. È quindi vantaggioso riferirsi a coordinate polari sferiche
(r, θ, φ)
come in gura 3.1.
Si ha
x =
r sin θ cos φ
y
z
r sin θ sin φ
r cos θ .
=
=
Con una trasformazione di coordinate, e ricordando la 2.11, il laplaciano diviene
2
∇
=
1 ∂
r2 ∂r
1
∂
∂
1
∂2
2 ∂
=
r
+ 2
sin θ
+ 2 2
∂r
r sin θ ∂θ
∂θ
r sin θ ∂φ2
=
∇2r +
1 2
1 L̂2
∇θ,φ = ∇2r − 2 2 ;
2
r
r l'equazione agli autovalori associata all'equazione di Schrödinger stazionaria si scrive per una particella
di massa
µ:
∂2
∂
2 1 ∂
1
∂
1
2 ∂
−
ψ + U (r)ψ = Eψ .
r
+ 2
sin θ
+ 2 2
2µ r2 ∂r
∂r
r sin θ ∂θ
∂θ
r sin θ ∂φ2
Cerchiamo soluzioni del tipo
ambo i membri per
RΘΦ
ψ(r, θ, φ) = R(r)Θ(θ)Φ(φ);
(3.1)
inserendo nell'espressione (3.1) e dividendo
ottieniamo:
1 d2 Φ
sin2 θ d
=
−
Φ dφ2
R dr
sin θ d
dΘ
2µ
2 dR
r
−
sin θ
− 2 r2 sin2 θ[E − U (r)] .
dr
Θ dθ
dθ
(3.2)
3.1 Potenziali a simmetria sferica
21
Figura 3.1: Coordinate polari sferiche.
Il primo membro dipende solo da
φ,
il secondo da
separazione:
r
e
θ;
si ha dunque, chiamata
−m2&
d2 Φ
= −m2& Φ .
dφ2
la costante di
(3.3)
Si può vericare che la (3.3) è risolta da funzioni del tipo
Φ(φ) = eim φ
Φ(0) = Φ(2π)
se imponiamo che
(univocità) abbiamo che
m&
deve essere intero.
Per il secondo membro della (3.2) si ha
−
1 d
R dr
d
dR
m2
1
dΘ
2µ
r2
−
sin θ
− 2 r2 [E − U (r)] = − 2&
dr
Θ sin θ dθ
dθ
sin θ
(3.4)
che può venire riscritta come
1 d
R dr
m2&
1
2µ 2
d
dΘ
2 dR
−
r
+ 2 r [E − U (r)] =
sin θ
.
dr
dθ
sin2 θ Θ sin θ dθ
Possiamo eguagliare entrambi i membri a una generica costante che chiamiamo
1 d
dΘ
m2 Θ
−
sin θ
+ &2 = 8(8 + 1)Θ
sin θ dθ
dθ
sin θ
R
2µ
1 d
dR
r2
+ 2 [E − U (r)]R = 8(8 + 1) 2 .
r2 dr
dr
r
8(8 + 1);
(3.5)
otteniamo così
(3.6)
(3.7)
La risoluzione della (3.6) è un problema noto in matematica. Le soluzioni della (3.6), dette funzioni
P&m (cos θ), hanno signicato sico (danno luogo a una ψ nita) solo per 8 ∈ Z e 8 ≥ |m& |.
Complessivamente dunque la parte angolare ha la forma:
di Legendre
Y&,m (θ, φ) = Θ&,m (θ)Φm (φ) = N&,m P&m (cos θ)eim φ
(3.8)
3.1 Potenziali a simmetria sferica
22
Figura 3.2: Diagrammi polari per la dipendenza direzionale della densità di probabilità per
e
m = ±l.
8 = 1, 2, 3, 4
N&,m è una costante di normalizzazione, mentre le P&m (cos θ) sono le funzioni di Legendre. Le
Y&,m (θ, φ) sono dette armoniche sferiche: di seguito sono scritte quelle degli ordini più bassi. In genere,
seguendo la nomenclatura della convenzione atomica, lo stato a 8 = 0 viene detto stato s, lo stato 8 = 1
viene detto stato p, ecc.
1
Y0,0 =
(4π)1/2
1/2
1/2
3
3
Y1,0 =
cos θ ; Y1,±1 = ∓
e±iφ sin θ
4π
8π
1/2
1/2
1/2
5
15
15
2
±iφ
Y2,0 =
(3 cos θ − 1) ; Y2,±1 = ∓
e
sin θ cos θ ; Y2,±2 =
e±2iφ sin2 θ .
16π
8π
32π
dove
m2& = (−1/Φ)d2 Φ/dφ2 ; si ha
1 d
dΘ
1 d2 Φ Θ
−
= 8(8 + 1)Θ
sin θ
−
sin θ dθ
dθ
Φ dφ2 sin2 θ
Inseriamo nell'equazione (3.6) la (3.3)
che, moltiplicando per
RΦ,
dà
1 d
−
sin θ dθ
dψ
1 d2 ψ
= 8(8 + 1)ψ
sin θ
−
dθ
sin2 θ dφ2
e, tenuto conto della (2.11),
L̂2
ψ = 8(8 + 1)ψ .
2
Gli autovalori del quadrato del momento angolare sono quindi pari a
8(8 + 1)2 ,
in disaccordo con il
modello di Bohr.
Nelle gure 3.2 e 3.3 si mostrano i diagrammi polari corrispondenti alle densità di probabiltà associate
Θ∗ Θ (la densità
alle armoniche sferiche. Nei diagrammi polari la distanza dall'origine è proporzionale a
di probabilità non dipende da
φ).
3.2 L'atomo d'idrogeno
23
Figura 3.3: Diagrammi polari per la dipendenza direzionale della densità di probabilità per
m& = 0, ±1, ±2, ±3.
3.2
8=3
e e
L'atomo d'idrogeno
Passiamo ora ad analizzare i sistemi idrogenoidi: un elettrone legato dalla forza elettrostatica ad un
nucleo carico positivo. Tali sistemi costituiscono la base di molti studi chimico-sici.
−27
I parametri sici in gioco sono la massa del protone mp 1.67×10
kg, la massa dell'elettrone me −31
−19
kg, la carica elettrica dell'elettrone e del protone che in valore assoluto vale e 1.6 × 10
9.1 × 10
C. Il sistema protone-elettrone dell'atomo d'idrogeno si può considerare, come d'abitudine in meccanica,
me mp
alla stregua di una particella di massa pari alla massa ridotta µ = m +m orbitante intorno a un punto
e
p
sso in un sistema inerziale.
Dato che la massa
me
dell'elettrone è circa 1/2000 della massa
mp
del
protone, la massa ridotta coincide con la massa dell'elettrone entro una parte su 2000. La particella di
massa
µ
è sottoposta al potenziale a simmetria sferica della legge di Coulomb
U (r) = −
Poniamo per semplicità
Z=1
e2 Z
.
4π0 r
(atomo d'idrogeno).
L'equazione di Schrödinger in coordinate polari sferiche per il sistema elettrone-protone si scrive:
−
2 2
∇ ψ(r, θ, φ) + U (r)ψ(r, θ, φ) = Eψ(r, θ, φ) .
2µ
ψ è fattorizzabile come R(r)Y&,m (θ, φ);
R(r) deve soddisfare all'equazione
1 d
e2
2µ
R
2 dR
r
+ 2 E+
R = 8(8 + 1) 2 .
2
r dr
dr
4π0 r
r
Per quanto visto nella sezione precedente la
Y&,m (θ, φ)
la parte angolare
è data dalle (3.8) e la
(3.9)
3.2 L'atomo d'idrogeno
Denito il
24
2
raggio di Bohr a0 = 4π0 e2 µ 53 pm, si ha che le soluzioni radiali sono quantizzate:
&
Rnl (r/a0 ) = Nnl e−r/2a0 (r/a0 ) L̃2l+1
n+1 (r/a0 )
Nnl è un coeciente di
n > l sono accettabili.
dove
con
normalizzazione e gli
L̃
sono detti polinomi di Laguerre. Solo le soluzioni
Con i loro numeri quantici, le soluzioni dell'equazione di Schrödinger per l'atomo d'idrogeno possono
venire scritte
ψn,l,m (r, θ, φ) = Rn,l (r)Θ&,m (θ)Φm (φ)
dove gli indici
n, l, m&
sono i numeri quantici necessari a descrivere le soluzioni.
I numeri quantici
permessi sono:
n
8
m&
numero quantico principale
1, 2, 3, ...
n−1
±1, ±2, ..., ±l
numero quantico del momento angolare
0, 1, 2,...,
numero quantico magnetico
0,
Di seguito elenchiamo le funzioni d'onda corrispondenti ai primi numeri quantici.
.
Capitolo 5
La sica quantistica in un quadro
(in)formale
Non vi era evidenza che la topologia naturale degli spazi hilbertiani consentisse di render conto
dell'apparizione dell'atto libero; non era neppure certo che al momento si potesse porre il problema, se
non in termini estremamente metaforici.
Michel Houellebecq
Le particelle elementari
L'assiomatizzazione della sica quantistica è una sda che è stata lanciata da alcuni fra i più grandi
ingegni del secolo (Heisenberg, Bohm, von Neumann solo per citarne alcuni). Il fatto che esistano ancor
oggi accese discussioni chiarisce che non esiste una soluzione che abbia raccolto consenso universale.
Questo capitolo non ha l'ambizione di formalizzare un'assiomatica, ma solo di inquadrare in un quadro
formale più soddisfacente gli elementi per i quali un'euristica è stata formulata nei capitoli precedenti.
5.1
Funzione d'onda e spazi di Hilbert
Nell'interpretazione probabilistica di una funzione d'onda
Ψ(r, t)
di una particella, il dierenziale
|Ψ(r, t)|2 dV = Ψ∗ (r, t)Ψ(r, t) dV
rappresenta la probabilità di trovare la particella nel volume
dV ,
(5.1)
intorno del punto
r,
al tempo
t.
La
probabilità complessiva di trovare la particella da qualche parte nello spazio è uguale a 1, e dunque
dev'essere:
dV |Ψ(r, t)|2 = 1
(5.2)
dove l'integrale si estende su tutto lo spazio accessibile alle particelle. Per poter imporre la condizione di
normalizzazione, ci riconduciamo allora allo studio dell'insieme
L2
delle
funzioni a quadrato sommabile,
ossia l'insieme delle funzioni per le quali l'integrale (5.2) converge.
spazio vettoriale sul campo dei numeri complessi C; infatti:
∃ un'addizione + interna a L2 tale che (L2 ,+) è un gruppo abeliano, ossia:
L'insieme
•
L2
ha la struttura di
5.2 Osservabili e operatori
81
è commutativa;
è associativa;
zero e indicato con 0);
∀ Ψ ∈ L2 ∃ Φ ∈ L2 tale che Ψ + Φ = 0; Φ è detto opposto di Ψ e indicato con −Ψ;
∃ una moltiplicazione degli elementi di L2 per uno scalare, cioè un elemento del campo, tale che:
ammette un unico elemento neutro (detto
•
è distributiva rispetto all'addizione:
∀ c, c1 , c2 ∈ C, Ψ, Ψ1 , Ψ2 ∈ L2
c(Ψ1 + Ψ2 ) = cΨ1 + cΨ2 ;
(c1 + c2 )Ψ = c1 Ψ + c2 Ψ;
vale la proprietà:
∀ c1 , c2 ∈ C, Ψ ∈ L2
c1 (c2 Ψ) = (c1 c2 )Ψ.
Su
L2
deniamo il prodotto scalare
(Ψ, Φ)
come
(Ψ, Φ) =
il quale è tale che
∀ Ψ, Φ1 , Φ2 ∈ L2 , λ1 , λ2 ∈ C
∗
• (Ψ, Φ) = (Φ, Ψ)
V
dV Ψ∗ (r, t)Φ(r, t)
(5.3)
:
;
• (Ψ, λ1 Φ1 + λ2 Φ2 ) = λ1 (Ψ, Φ1 ) + λ2 (Ψ, Φ2 ).
e induce su
L2
la norma
2
|Ψ| = (Ψ, Ψ) ≥ 0.
Uno spazio vettoriale normato è detto
Hilbert su
C
(con la norma quadrata
spazio di Hilbert; allora possiamo dire che L2 è uno spazio di
| Ψ |2 ).
Osserviamo che vale la disuguaglianza triangolare di Schwarz:
| Ψ + Φ |2 ≤ | Ψ |2 + | Φ |2 .
5.2
Osservabili e operatori
operatore lineare
M̂ su L2 è un ente matematico che associa a una funzione Ψ di L2 la funΨ tramite una corrispondenza lineare M̂ : Ψ = M̂ Ψ tale che ∀ Ψ1 , Ψ2 ∈ L2 , λ1 , λ2 ∈ C
M̂ (λ1 Ψ1 + λ2 Ψ2 ) = λ1 M̂ Ψ1 + λ2 M̂ Ψ2 .
Un
zione
Vogliamo ora rappresentare gli osservabili tramite operatori, cosicché come ad uno stato sico corrisponde una funzione d'onda
Ψ(r, t),
così all'operazione di misura corrisponda un operatore lineare
M̂ .
Richiediamo che tale operatore lineare sia hermitiano (o autoaggiunto).
5.2.1 Operatori hermitiani
+
tale che
Si denisce operatore aggiunto di M̂ l'operatore M̂
∀ Ψ, Φ ∈ L2 (M̂ + Ψ, Φ) = (Ψ, M̂ Φ)
Un operatore lineare
M̂
si dice
(5.4)
autoaggiunto o hermitiano se M̂ + = M̂ , cioè se ∀ Ψ, Φ ∈ L2
(M̂ Ψ, Φ) = (Ψ, M̂ Φ)
(5.5)
5.2 Osservabili e operatori
82
ovvero
dV Ψ∗ (M̂ Φ) =
dV (M̂ Ψ)∗ Φ
(5.6)
Si deniscono anche la somma e il prodotto di operatori, nel modo seguente:
Somma:
= (Â + B)
è tale che
C
= (Â + B)Ψ
= ÂΨ + BΨ
CΨ
∀ Ψ ∈ L2
(5.7)
Consegue dalla denizione di operatore aggiunto che la somma di due operatori hermitiani è ancora un
operatore hermitiano.
Prodotto:
= (ÂB)
è tale che
C
= (ÂB)Ψ
= Â(BΨ)
CΨ
∀ Ψ ∈ L2
(5.8)
Da questa denizione segue che l'operatore aggiunto del prodotto di due operatori
Infatti:
(Ψ, (ÂB)Φ)
=
+
(ÂB)
è
+ Â+ .
B
=
dV Ψ (Â(BΦ)) ==
dV (Â+ Ψ)∗ (BΦ)
V
+ (Â+ Ψ))∗ Φ = ((B
+ Â+ )Ψ, Φ)
=
dV (B
∗
V
V
Osserviamo che, in generale,
= (B
Â).
(ÂB)
Per esempio,
px (xΨ) = x(
px Ψ)
poiché
∂Ψ
∂(xΨ)
= x −i
−i
∂x
∂x
Vediamo due esempi di operatori autoaggiunti.
Esempio 1.
Esempio 2.
Dato che
L'operatore posizione
rˆ,
corrispondendo a una terna di numeri reali, è hermitiano.
pˆ = −i∇, è hermitiano.
pˆ = (p̂x , 0, 0) + (0, p̂y , 0) + (0, 0, p̂z ), limitiamoci a dimostrare
L'operatore quantità di moto
che
p̂x
(per esempio) è
autoaggiunto:
(Ψ, p̂x Φ) =
poiché
+∞
+∞
−∞
[Ψ∗ Φ]−∞ = 0
+∞
∂Φ(x)
∂Ψ∗
dx Ψ∗ (x) −i
−
dx
−iΦ(x)
= [Ψ∗ Φ]+∞
=
−∞
∂x
∂x
−∞
∗
+∞
∂Ψ(x)
dx −i
Φ(x) = (p̂x Ψ, Φ)
=
∂x
−∞
dal momento che le due funzioni sono a quadrato sommabile.
5.2.2 Relazioni di commutazione
l'operatore [Â, B]
− (talora più brevemente indicato
Si denisce commutatore di due operatori  e B
come [Â, B]) mediante la relazione [Â, B]− = (ÂB − B Â), e si dice che due operatori commutano
quando il loro commutatore è l'operatore nullo.
5.3 Notazione di Dirac
B
83
Il commutatore di due operatori è hermitiano solo quando è l'operatore nullo. Se i due operatori
Â
e
sono autoaggiunti, si ha infatti:
+ = (ÂB
−B
Â)+
[Â, B]
−
+ = B
+ Â+ − Â+ B
 − ÂB
= −[Â, B]
−
=B
Analogamente, si denisce
+B
Â),
(ÂB
+ come [Â, B]
+=
anticommutatore di due operatori  e B l'operatore [Â, B]
Â
che è sempre autoaggiunto se i due operatori
e
B
sono autoaggiunti. Si ha infatti:
+ = (ÂB
+B
Â)+
[Â, B]
+
+ = B
+ Â+ + Â+ B
 + ÂB
= [Â, B]
+
=B
Osserviamo che
=
ÂB
1
+ + 1 [Â, B]
−
[Â, B]
2
2
e dunque che il prodotto di due operatori hermitiani è hermitiano se e solo se gli operatori commutano.
Ân di un operatore è un operatore autoaggiunto.
r) = p2 /2m + U (r) = −2 ∇2 /2m + U (r) è hermitiano,
L'operatore hamiltoniano H(
In particolare, la generica potenza
Esempio 3.
perché lo sono la somma e le potenze di operatori hermitiani.
5.3
Notazione di Dirac
notazione di Dirac per gli spazi vettoriali, un vettore dello spazio è identicato dal simbolo | Φ >,
ket, mentre il simbolo < Ψ | è chiamato bra.
La loro giustapposizione forma il bracket < Ψ | Φ >, che rappresenta il prodotto scalare dei due
Nella
ed è chiamato
vettori:
< Ψ | Φ > = (Ψ, Φ) =
In questa notazione, ogni operatore
Â
agisce su un ket
dunque
< Ψ | Â | Φ > =
Il duale di
5.4
 | Φ >
è
[ Â | Φ > ]∗ = < Â Φ |
dV Ψ∗ Φ .
| Φ >
, e lo trasforma nel ket
 | Φ >
, e
dV Ψ∗ (ÂΦ) .
.
Autovalori e autovettori di operatori hermitiani
5.4.1 Valore d'aspettazione
Allo scopo di rappresentare le funzioni d'onda, l'insieme
L2
risulta, da un punto di vista sico, troppo
grande: le funzioni d'onda devono possedere alcune proprietà di regolarità, in relazione al signicato
2
attribuito a |Ψ(r, t)| .
Possiamo validamente ritenere che le funzioni
Ψ(r, t)
adatte a denire gli stati sici siano denite
in qualunque punto interno al dominio (esclusi al più punti di frontiera a misura nulla), continue, e
dierenziabili innite volte (per esempio, lo stato la cui funzione d'onda fosse discontinuo in un dato
punto dello spazio non ha signicato sico, dato che nessun esperimento ci permette di avere accesso
−30
a fenomeni reali su scala molto piccola, dell'ordine di 10
m). Possiamo anche ridurci a considerare
5.4 Autovalori e autovettori di operatori hermitiani
84
le funzioni d'onda che hanno un dominio limitato (per avere la certezza che una particella possa essere
trovata dentro una regione nita dello spazio, per esempio dentro un laboratorio).
Senza dare una lista precisa e completa di queste condizioni supplementari, chiamiamo
(contenuto in
L2 )
H
l'insieme
delle funzioni d'onda adatte a descrivere le evidenze siche.
Formuliamo a questo punto due postulati.
•
Lo stato di una particella ad un tempo
•
L'operazione di misura è rappresentata dall'applicazione di un operatore hermitiano
∈ H.
t è rappresentato da una funzione
d'onda (un ket)
Â
| Ψt (r) >
ad un ket:
 | Ψt (r) >
e il valore di aspettazione (valore medio o valore atteso) di una operazione di misura è
A = < Ψt (r) | Â | Ψt (r) > .
Si dice che l'operatore
Â
è
in sandwich nel bracket < Ψt (r) | Â | Ψt (r) > (=
V
dV Ψt (r)∗ ÂΨt (r)).
Osserviamo che il formalismo che abbiamo scelto è tale che i risultati delle misure sono numeri reali;
infatti:
Lemma 1 ∀ Ψ, Φ ∈ H
Dimostrazione.
< Ψ | Â | Φ > = < Φ | Â+ | Ψ >∗
< Ψ | Â | Φ > = < Ψ | ÂΦ > = < ÂΦ | Ψ >∗ =
= < Φ | Â+ Ψ >∗ = < Φ | Â+ | Ψ >∗
✷
Teorema 1 Il valor medio A di un'osservabile  è reale.
Dimostrazione. Grazie al Lemma 1 e all'hermiticità di Â
A = < Ψ | Â | Ψ > = < Ψ | Â+ | Ψ >∗
= < Ψ | Â | Ψ >∗ = A ∗
✷
Si denisce lo
scarto (spread) ∆ dell'operatore  la dierenza ∆ =  − A; esso indica quanto una
singola misura si discosti dal valore di aspettazione. Evidentemente
2
in quel caso lo è anche (∆Â) .
(∆Â)2 = < Ψ | (∆Â)2 | Ψ > ≥ 0 (forma
interessati a cercare quegli stati ΨA per i quali
∆Â
è hermitiano quando lo è
Osserviamo che
semidenita positiva).
Siamo ora
lo scarto si annulla (ove
A
< ΨA | ∆ | ΨA > = 0
< Ψ | Ψ > = 1,
(Â − A) | Ψ > = 0 ⇒ < Ψ | (Â − A) | Ψ > = 0 ⇒ Â | Ψ > = A | Ψ >
cioè vogliamo risolvere l'equazione agli autovalori
 | Ψ > = A | Ψ >
con
A
una costante (reale!).
Postuliamo allora:
e
è una costante),
cioè tali che:
Dato che ipotizziamo che
Â,
5.5 Sviluppo in serie di un operatore
•
•
85
che i possibili risultati di una misura siano gli autovalori dell'operatore che la rappresenta (cioè che
 | Ψ > = A | Ψ >),
e
che immediatamente dopo la misura che ha dato come risultato l'autovalore
A
il sistema sia in uno
stato corrispondente a quell'autovalore.
Sia
Ai , i ∈ N
l'insieme degli autovalori dell'operatore
Â.
Teorema 2 Le autofunzioni relative ad autovalori diversi sono ortogonali.
Dimostrazione. Siano Ψm , Ψn, Am , An tali che n = m ⇒ Am = An e
 | Ψm > = Am |Ψm >
 | Ψn > = An |Ψn >
Allora
An < Ψn | Ψm > = < Ψn | Â | Ψm > = Am < Ψn | Ψm >
⇒ 0 = (An − Am ) < Ψn | Ψm >
⇒ < Ψn | Ψm > = 0 ∀ m = n .✷
Con la opportuna normalizzazione, si ottiene che
< Ψn | Ψm > = δmn
dove
δmn
è la funzione
delta di Kronecker, che vale 1 se m = n e 0 se m = n.
Naturalmente alcuni autovalori possono essere degeneri, e corrispondere a più autovettori indipendenti.
5.5
Sviluppo in serie di un operatore
Si dimostra che le autofunzioni di un operatore hermitiano costituiscono una base completa per lo spazio
di Hilbert delle possibili funzioni d'onda a un tempo t. A partire da una base completa, è sempre possibile
costruire una base ortonormale dello spazio (metodo di Gram-Schmidt), sicché
I=
| Ψm > < Ψm | .
(5.9)
m
(relazione di completezza).
Questo signica che una qualunque funzione d'onda può essere rappresentata in questa base
ortonormale da un'unica combinazione lineare degli elementi della base:
|Ψ >=
| Ψm > < Ψm | Ψ > =
m
(i
< Ψ m | Ψ > = cm
cm | Ψ m >
m
sono numeri).
La normalizzazione del modulo quadro della
1 =< Ψ|Ψ >=
|Ψ >
a 1 equivale a una relazione sulle
< Ψ| Ψm > < Ψm |Ψ >=
m
e la probabilità di ottenere da una misura l'autovalore
cm :
2
|cm | ,
m
am
vale
2
Pm = | < Ψm |Ψ > | = |cm |2 .
Inoltre, esistono coecienti
 | Ψ > =
mn
amn = < Ψm | Â | Ψn >
tali che:
| Ψm > < Ψm | Â | Ψn > < Ψn | Ψ > =
amn cn | Ψm > .
m,n
[amn ] è una matrice quadrata (innita), che rappresenta l'operatore  sullo spazio di Hilbert L2
cn sono una n-tupla di componenti del vettore che rappresenta la |Ψ >.
matriciale; le
in forma
5.6 Misura simultanea di osservabili diverse
5.6
Siano
86
Misura simultanea di osservabili diverse
Â
e
B
due operatori hermitiani; deniamo
resto di commutazione di  e B l'operatore C tale che
− = iC
[Â, B]
Osserviamo che
C
è hermitiano:
⇒
= 1 [Â, B]
−
C
i
+ = − 1 (−[Â, B]
− ) = 1 [Â, B]
−=C
+ = − 1 [Â, B]
C
−
i
i
i
Si ha anche che
− = [(Â − A), (B
− B)]− =
[∆Â, ∆B]
− B) − (B
− B)(Â − A) =
= (Â − A)(B
− AB
− B Â + AB) − (B
 − B  − AB
+ AB) =
= (ÂB
−B
Â)
= (ÂB
− = iC
− = [Â, B]
=⇒ [∆Â, ∆B]
Sia
I(α) =
2
dV |(α∆ − i∆B)Ψ|
Allora
con un generico
I(α) =
=
dV
∗ (α∆ − i∆B)Ψ
=
(α∆ − i∆B)Ψ
dV
=
α ∈ R; I(α) ≥ 0∀ α ∈ R.
dV
Ψ=
Ψ∗ (α∆ + i∆B)(α∆
 − i∆B)
 − ∆Â∆B)
+ (∆B)
2 Ψ =
Ψ∗ α2 (∆Â)2 + iα(∆B∆
+ (∆B)
2 Ψ ≥0
= dV Ψ∗ α2 (∆Â)2 + αC
In più,
0 ≤ I(α) =
dV
+ (∆B)
2 Ψ =
Ψ∗ α2 (∆Â)2 + αC
2 |Ψ> +α<Ψ|C
|Ψ>=
= α2 < Ψ | (∆Â)2 | Ψ > + < Ψ | (∆B)
C
= (∆A)2 α2 + α
+ (∆B)2 =
(∆A)2
2
2
C
C
C
2
= (∆A)2 α + α
+
=
+ (∆B)2 −
(∆A)2
4(∆A)4
4(∆A)2
2
2
C
C
+ (∆B)2 −
∀α∈R
= (∆A)2 α +
2(∆A)2
4(∆A)2
⇒ (∆B)2 −
C
2
4(∆A)2
2
≥0 ⇔
(∆A)2 (∆B)2 ≥
C
.
4
5.7 Evoluzione temporale dei valori medi
87
Questo signica che se due osservabili non commutano tra loro, non possono essere misurate
contemporaneamente con precisione arbitraria.
Esempio.
[p̂x x
] =
Posizione e quantità di moto.
∂x·
∂
∂
∂
∂
+ 1(−i) − x −i
−i , x = −i
− x −i
= −xi
= −i
∂x
∂x
∂x
∂x
∂x
dunque
(∆px )2 (∆x)2 ≥
2
4
che può scriversi come
∆px ∆x ≥
2
(principio di indeterminazione di Heisenberg per posizione e impulso).
5.6.1 L'operatore momento angolare
In analogia con la meccanica classica, l'operatore momento angolare è denito dalla
ˆ
L = rˆ × pˆ .
Si osserva che l'operatore è hermitiano. Il quadrato dell'operatore
L̂2 = L̂2x + L̂2y + L̂2z
è anch'esso hermitiano.
Valgono le seguenti proprietà di commutazione:
L̂x , L̂y = iL̂z ; L̂y , L̂z = iL̂x ; L̂z , L̂x = iL̂y
L̂2 , L̂x = [L̂2 , L̂y ] = [L̂2 , L̂z ] = 0
e quindi è impossibile misurare contemporaneamente con precisione due componenti diverse del momento
angolare, mentre è possibile misurare contemporaneamente con arbitraria precisione il quadrato del
momento angolare e la proiezione su un asse coordinato.
5.7
Evoluzione temporale dei valori medi
Si postula che
•
L'evoluzione temporale di uno stato sia regolata dall'equazione di Schrödinger
i
con
Ĥ
∂
|Ψ >= Ĥ|Ψ > ,
∂t
denito come nel capitolo precedente, e con le denizioni di momento e posizione del capitolo
precedente.
5.8 Simmetrie
88
Consideriamo un operatore hermitiano
della quantità
A
Â
non esplicitamente dipendente dal tempo.
∂
∂ Ā
=
< Ψ | Â | Ψ >=
∂t
∂t
e, poiché dall'equazione di Schrödinger
dĀ
=
dt
Il valor medio
dipenderà in generale dal tempo tramite la
∂Ψ ∂Ψ
Â Ψ + Ψ Â ∂t
∂t
i∂Ψ/∂t = ĤΨ
e
Ĥ
è hermitiano,
−i
i
−i
i
ĤΨ Â Ψ + Ψ Â ĤΨ =
ΨĤ Â Ψ − Ψ Â ĤΨ =
i
i
=
< Ψ|Ĥ Â|Ψ > − < Ψ|ÂĤ|Ψ > = < Ψ|[Ĥ, Â]|Ψ >
Quindi
i
dĀ
= [Ĥ, Â] .
dt
5.7.1 Commutazione con l'Hamiltoniano e invarianza
Come corollario del fatto che la derivata del valore di aspettazione di un'osservabile rispetto al tempo
è il valore di aspettazione del commutatore dell'Hamiltoniano con l'operatore associato all'osservabile
si ha il fatto che se un operatore commuta con l'hamiltoniano il valore di aspettazione dell'osservabile
associata è una costante del moto. Questo fatto mostra un'interessante analogia con il teorema di Nöther
in meccanica classica.
In particolare l'Hamiltoniano commuta con se stesso; quindi, se non è dipendente esplicitamente dal
tempo, l'osservabile ad esso associata (l'energia) si conserva.
Se
∂U/∂x = 0
l'operatore
pˆx
commuta con
Ĥ ;
proprietà analoghe valgono per
pˆy
e
pˆz .
In assenza di
forze esterne, la quantità di moto si conserva.
In presenza di forze centrali, dunque dipendenti solo da
polari sferiche è funzione soltanto di
θ
e
φ)
r,il
momento angolare (che in coordinate
commuta con l'hamiltoniano: dunque il momento angolare
si conserva.
5.8
Simmetrie
Se l'hamiltoniano è invariante per l'applicazione di un operatore di simmetria, esso commuta con
l'operatore stesso (quindi è denibile una opportuna costante del moto: ritroviamo il teorema di Nöther).
Ciò ha un'applicazione particolare nel caso delle cosiddette
numero nito di autovalori.
Consideriamo ad esempio l'operatore
simmetrie discrete,
che cioè hanno un
parità Π che agisce sulla base r mediante la trasformazione
Π|r >= | − r >
(in pratica scambia le coordinate
r
con
−r ).
L'operatore è tale che
Π2 = I
e dunque ammette autovalori
±1.
Un hamiltoniano invariante per riessione conserva la parità.
Analoghe considerazioni possono farsi per operatori come la coniugazione di carica
cariche delle particelle.
C
che scambia le
5.9 Rappresentazione
5.9
89
Rappresentazione
Cambiare rappresentazione signica cambiare base.
Teorema 3 Se due operatori  e B̂ commutano, e se |ψ > è un autovettore di Â, allora B̂|ψ > è anche
autovettore di  con lo stesso autovalore.
Si ha infatti
Â|ψ >= A|ψ >⇒ B̂ Â|ψ >= AB̂|ψ >
e dunque, sfruttando la commutazione
Â(B̂|ψ >) = A(B̂|ψ >)
✷
Ma allora
(B̂|ψ >) è proporzionale a |ψ > nel caso non degenere, o comunque appartiene allo stesso sot-
tospazio nel caso degenere: dunque se due osservabili commutano si può costruire una base ortonormale
H
per lo spazio
a partire da autovettori comuni ai due operatori.
In generale due operatori non commutano: dunque un cambiamento di rappresentazione costituisce un
cambiamento di base. Questo cambiamento può essere realizzato utilizzando le relazioni di completezza
(5.9).
Due rappresentazioni particolarmente utilizzate sono quelle sulla base
e sulla base
p
r degli autovettori della posizione
degli autovettori del momento.
5.9.1 Insiemi completi di osservabili compatibili
Per denizione un insieme di osservabili costituisce un insieme completo di osservabili compatibili se:
•
•
Tutte le osservabili commutano a coppie;
Specicare gli autovalori di tutte le osservabili determina un unico autovettore (a meno di fattori
moltiplicativi): l'insieme di osservabili rimuove la degenerazione.
Problemi
1. Per l'operatore momento angolare, calcolare i seguenti commutatori:
• L̂2 , L̂x
• L̂x , L̂y
• L̂x , L̂z
2. Per una particella di massa
m
sottoposta a una forza gravitazionale, tale che
Ĥ =
con
G
e
M
pˆ2
mM
−G
2m
r
costanti, dimostrare che il momento angolare rispetto all'origine si conserva.