UNITÀ 15 • La luce
Che cosa accade se la luce colpisce un ostacolo opaco circolare molto piccolo?
Basandosi sul modello ondulatorio ed
estrapolando le conseguenze legate alla diffrazione, al centro dell’ombra prodotta da
un disco, essendo uguale il percorso compiuto dai raggi secondari lungo il bordo, si
dovrebbe formare un punto luminoso.
Questo fenomeno è del tutto incompatibile con il modello corpuscolare, secondo
cui l’ostacolo circolare avrebbe dovuto intercettare i raggi luminosi, dando luogo a
un cerchio scuro.
Questa previsione della teoria ondulatoria fu confermata nel 1818, presso l’Accademia di Parigi, da un esperimento che non solo consentì ad Augustin Jean
Fresnel (1788-1827) di ottenere il primo premio del concorso a cui partecipava, ma che soprattutto convinse uno scienziato influente come S.D. Poisson
(1781-1840), che faceva parte della commissione giudicante, della validità
dell’ipotesi ondulatoria sostenuta da Fresnel.
FLASH
I contorni degli oggetti
Fresnel ipotizzò che al centro
dell’ombra di un piccolo oggetto
colpito dalla luce si doveva formare un punto luminoso centrale a causa della natura ondulatoria della luce, cosa che venne
confermata sperimentalmente.
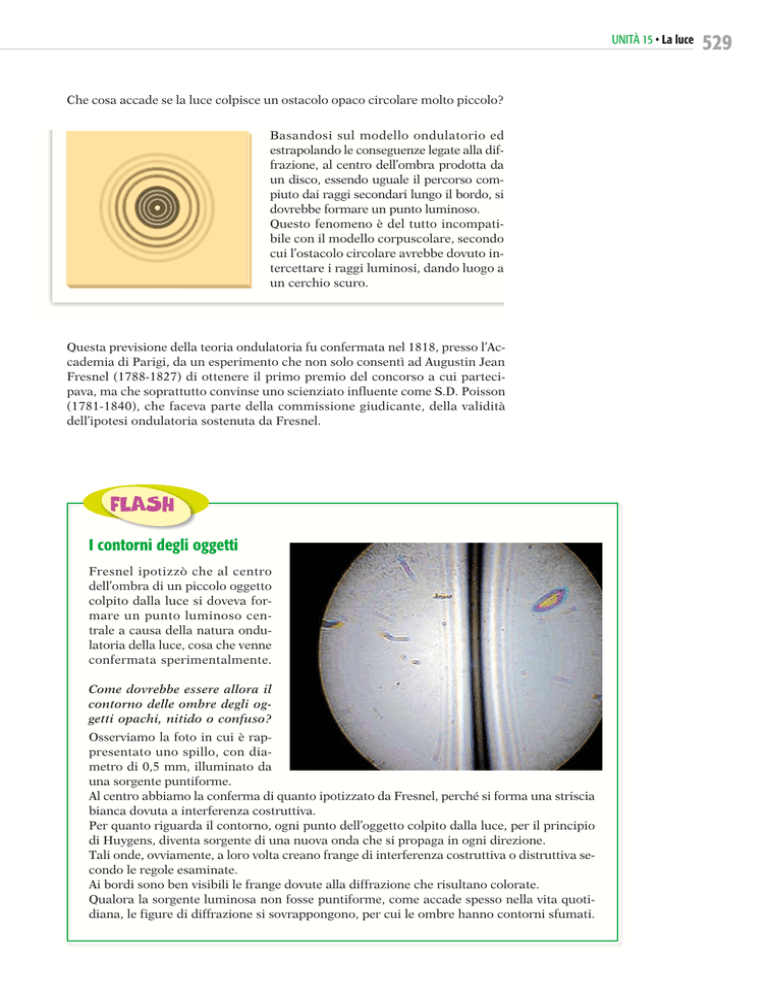
Come dovrebbe essere allora il
contorno delle ombre degli oggetti opachi, nitido o confuso?
Osserviamo la foto in cui è rappresentato uno spillo, con diametro di 0,5 mm, illuminato da
una sorgente puntiforme.
Al centro abbiamo la conferma di quanto ipotizzato da Fresnel, perché si forma una striscia
bianca dovuta a interferenza costruttiva.
Per quanto riguarda il contorno, ogni punto dell’oggetto colpito dalla luce, per il principio
di Huygens, diventa sorgente di una nuova onda che si propaga in ogni direzione.
Tali onde, ovviamente, a loro volta creano frange di interferenza costruttiva o distruttiva secondo le regole esaminate.
Ai bordi sono ben visibili le frange dovute alla diffrazione che risultano colorate.
Qualora la sorgente luminosa non fosse puntiforme, come accade spesso nella vita quotidiana, le figure di diffrazione si sovrappongono, per cui le ombre hanno contorni sfumati.
529
530
MODULO 5 • Le onde
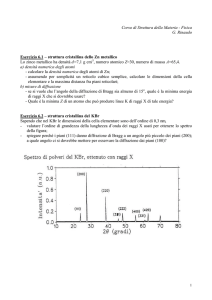
15.8 Il potere risolutivo
frange di diffrazione
C
P
θ
fascio di luce
S
schermo
schermo
con foro
sorgente
Quando si fa passare la luce attraverso un foro S circolare, anziché attraverso
una fenditura rettilinea, si creano delle frange di diffrazione di forma circolare e concentriche rispetto al centro C. La zona maggiormente luminosa è
costituita dal disco centrale. Se λ è la lunghezza d’onda della luce e D è il diametro del foro, che deve essere sufficientemente piccolo, il punto medio P della
prima frangia scura è tale che il segmento SP forma con SC un angolo dato
dalla seguente formula:
senθ ≅ 1, 22
λ
D
Se si hanno due sorgenti di luce puntiformi poste a una certa distanza ds, ciascuno dei due fasci luminosi passando attraverso un piccolo foro circolare
produce la propria figura di diffrazione. Se i due centri luminosi sono molto
vicini (per cui ds è molto piccola), non è possibile distinguere fra loro le due
sorgenti, che appaiono come un’unica sorgente.
dS
Le due sorgenti di luce potrebbero essere i fari di un’auto in avvicinamento
oppure due stelle e il foro attraverso il quale passano i rispettivi fasci potrebbero essere la pupilla dell’occhio o l’apertura di uno strumento ottico. La condizione in base alla quale si può capire se le due sorgenti sono separate e distinguibili tra loro è il criterio di Rayleigh.
criterio di Rayleigh
Due sorgenti puntiformi sono distinguibili tra loro quando il massimo luminoso centrale della figura di diffrazione di una delle due sorgenti cade più lontano del primo minimo scuro delle frange dell’altra sorgente.
UNITÀ 15 • La luce
Indicando con θ l’angolo tra le due sorgenti e con D il diametro di apertura
dell’obiettivo dello strumento (nel caso dell’occhio, il diametro della pupilla), e
potendo prendere sen θ ≅ θ in quanto l’angolo (misurato in radianti) è piccolo,
si ha che sulla base del criterio di Rayleigh il valore minimo di θ (angolo limite
di risoluzione θmin) affinché le due sorgenti vengano percepite come separate è:
θmin ≅ 1, 22
angolo limite
di risoluzione
λ
D
Come al solito, λ è la lunghezza d’onda della luce incidente. Il potere risolutivo, quindi, nel caso di un telescopio aumenta all’aumentare del diametro D
del suo obiettivo.
esempio
Prendiamo in considerazione l’occhio umano: ipotizziamo che il diametro
della pupilla sia di 2,0 mm (cioè 2,0 ⋅ 10−3 m) e che la lunghezza d’onda della
luce sia di 5,5 ⋅ 10−7 m (colore giallo).
dS
Cerchiamo l’angolo limite di risoluzione
per il quale il nostro occhio distingue
due oggetti.
θmin
L
Applichiamo la formula:
θ min ≅ 1, 22
λ
D
dove la lunghezza d’onda da considerare è quella relativa al mezzo nel quale si
osserva la diffrazione e quindi, per l’occhio umano, si deve utilizzare λ/1,36.
Sostituendo i valori troviamo:
θ min ≅ 1, 22
5, 5 ⋅ 10 −7 m
d = 0, 014°
= 2, 5 ⋅ 10 −4 rad
1,36 ⋅ 2,0 ⋅ 10 −3 m
Ovviamente, a parità di distanza fra le due sorgenti, quanto più esse sono lontane dall’osservatore, tanto più è difficile per l’occhio umano vederle fra loro
distinte. In particolare, se due sorgenti di luce gialla (che possono essere due
lampadine) si trovano a L = 200 m dall’occhio, per vederle separate tra di loro
ci deve essere una distanza dS pari almeno a:
dS = L ⋅ tan θmin
ma per θmin piccolo si ha:
tan θmin ≅ θmin
quindi:
dS ≅ L ⋅ θmin
e sostituendo i dati:
dS ≅ 200 ⋅ 2,5 ⋅ 10−4 = 0,050 m
La separazione fra le due lampadine deve essere almeno di 5,0 cm.
531